Borel-Cantelli lemma

2020 Mathematics Subject Classification: Primary: 60-01 Secondary: 60F1560F20 [MSN][ZBL]

A frequently used statement on infinite sequences of random events. Let 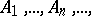be a sequence of events from a certain probability space and let 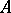be the event consisting in the occurance of (only) a finite number out of the events 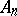, 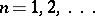. Then, according to the Borel–Cantelli lemma, if

(*)

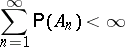then

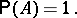If the events 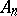are mutually independent, then 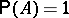or 0, depending on whether the series 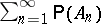converges or diverges, i.e. in this case the condition (*) is necessary and sufficient for 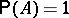; this is the so-called Borel criterion for "zero or one" (cf. Zero-one law). This last criterion can be generalized to include certain classes of dependent events. The Borel–Cantelli lemma is used, for example, to prove the strong law of large numbers.

References

[1]	E. Borel, "Les probabilités dénombrables et leurs applications arithmetique" Rend. Circ. Mat. Palermo (2) , 27 (1909) pp. 247–271
[2]	F.P. Cantelli, "Sulla probabilità come limite della frequenza" Atti Accad. Naz. Lincei , 26 : 1 (1917) pp. 39–45
[3]	M. Loève, "Probability theory" , Princeton Univ. Press (1963)

Comments

The Borel–Cantelli lemma can be used in number theory to prove the so-called "normality" of almost-all natural numbers, cf. [a1], Chapt. 8, Sect. 6.

References

[a1]	W. Feller, "An introduction to probability theory and its applications" , 1 , Wiley (1957) pp. Chapt.14