Difference between revisions of "Borel strong law of large numbers"
(60F15) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 18: | Line 18: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> E. Borel, "Les probabilités dénombrables et leurs applications arithmetique" ''Rend. Circ. Mat. Palermo (2)'' , '''27''' (1909) pp. 247–271</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> M. Kac, "Statistical independence in probability, analysis and number theory" , Math. Assoc. Amer. (1963) {{MR|1530983}} {{MR|0110114}} {{ZBL|0112.09101}} </TD></TR></table> |
Revision as of 10:29, 27 March 2012
2020 Mathematics Subject Classification: Primary: 60F15 [MSN][ZBL]
Historically, the first variant of the strong law of large numbers, formulated and proved by E. Borel [1] in the context of the Bernoulli scheme (cf. Bernoulli trials). Consider independent random variables 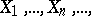 which are identically distributed and assume one of two values 0 and 1 with probability of 1/2 each; the expression
which are identically distributed and assume one of two values 0 and 1 with probability of 1/2 each; the expression 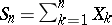 will then give the number of successful trials in a Bernoulli scheme in which the probability of success is 1/2. Borel [1] showed that
will then give the number of successful trials in a Bernoulli scheme in which the probability of success is 1/2. Borel [1] showed that
 |
with probability one as 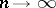 . It was subsequently (1914) shown by G.H. Hardy and J.E. Littlewood that, almost certainly,
. It was subsequently (1914) shown by G.H. Hardy and J.E. Littlewood that, almost certainly,
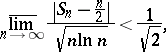 |
after which (1922) the stronger result:
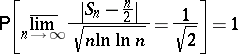 |
was proved by A.Ya. Khinchin. See also Law of the iterated logarithm.
References
| [1] | E. Borel, "Les probabilités dénombrables et leurs applications arithmetique" Rend. Circ. Mat. Palermo (2) , 27 (1909) pp. 247–271 |
| [2] | M. Kac, "Statistical independence in probability, analysis and number theory" , Math. Assoc. Amer. (1963) MR1530983 MR0110114 Zbl 0112.09101 |
Borel strong law of large numbers. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Borel_strong_law_of_large_numbers&oldid=20797