Difference between revisions of "User:Rafael.greenblatt/sandbox/Pfaffian"
| Line 11: | Line 11: | ||
$$ | $$ | ||
\left( | \left( | ||
| − | \begin{matrix | + | \begin{matrix} |
1 & 2 & \ldots & 2n-1 & 2n \\ | 1 & 2 & \ldots & 2n-1 & 2n \\ | ||
i_1 & j_1 & \ldots & i_n & j_n | i_1 & j_1 & \ldots & i_n & j_n | ||
| Line 20: | Line 20: | ||
A Pfaffian has the following properties: | A Pfaffian has the following properties: | ||
| − | + | #) $\text{Pf } (C^T X C) = (\det C) (\text{Pf } X)$ for any matrix $C$ of order $2n$; | |
2) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072500/p07250023.png" />; | 2) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072500/p07250023.png" />; | ||
Revision as of 14:17, 25 January 2012
of a skew-symmetric matrix $X$
The polynomial $\text{Pf } X$ in the entries of $X$ whose square is $\text{det } X$. More precisely, if $X = \|x_{ij}\|$ is a skew-symmetric matrix (i.e. $x_{ij}=-x_{ji}$, $x_{ii}=0$; such a matrix is sometimes also called an alternating matrix) of order $2n$ over a commutative-associative ring $A$ with a unit, then $\text{Pf } X$ is the element of $A$ given by the formula
$$ \text{Pf } X = \sum_s \varepsilon(s)x_{i_1j_1}\ldots x_{i_nj_n}, $$
where the summation is over all possible partitions $s$ of the set $\{1,\ldots,2n\}$ into non-intersecting pairs $\{i_\alpha,j_\alpha\}$, where one may suppose that $i_\alpha<j_\alpha$, $\alpha=1,\ldots,n$, and where $\varepsilon(s)$ is the sign of the permutation
$$ \left( \begin{matrix} 1 & 2 & \ldots & 2n-1 & 2n \\ i_1 & j_1 & \ldots & i_n & j_n \end{matrix} \right). $$
A Pfaffian has the following properties:
- ) $\text{Pf } (C^T X C) = (\det C) (\text{Pf } X)$ for any matrix $C$ of order $2n$;
2) 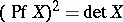 ;
;
3) if 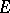 is a free
is a free 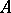 -module with basis
-module with basis 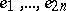 and if
and if
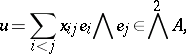 |
then
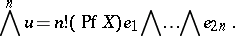 |
References
| [1] | N. Bourbaki, "Elements of mathematics. Algebra: Modules. Rings. Forms" , 2 , Addison-Wesley (1975) pp. Chapt.4;5;6 (Translated from French) |
Rafael.greenblatt/sandbox/Pfaffian. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rafael.greenblatt/sandbox/Pfaffian&oldid=20487