Difference between revisions of "User:Rafael.greenblatt/sandbox/Pfaffian"
From Encyclopedia of Mathematics
(Created page with "''of a skew-symmetric matrix $X$'' The polynomial $\text{Pf } X$ in the entries of $X$ whose square is $\text{det } X$. More precisely, if $X = \|x_{ij}\|$ is a skew-symmet...") |
|||
| Line 1: | Line 1: | ||
''of a skew-symmetric matrix $X$'' | ''of a skew-symmetric matrix $X$'' | ||
| − | The polynomial $\text{Pf } X$ in the entries of $X$ whose square is $\text{det } X$. More precisely, if $X = \|x_{ij}\|$ is a skew-symmetric matrix (i.e. $x_{ij}=-x_{ji}$, $x_{ii}=0$; such a matrix is sometimes also called an alternating matrix) of order $2n$ over a commutative-associative ring $A$ with a unit, then | + | The polynomial $\text{Pf } X$ in the entries of $X$ whose square is $\text{det } X$. More precisely, if $X = \|x_{ij}\|$ is a skew-symmetric matrix (i.e. $x_{ij}=-x_{ji}$, $x_{ii}=0$; such a matrix is sometimes also called an alternating matrix) of order $2n$ over a commutative-associative ring $A$ with a unit, then $\text{Pf } X$ is the element of $A$ given by the formula |
| − | + | $$ | |
| + | \text{Pf } X = \sum_s \varepsilon(s)x_{i_1j_1}\ldotsx_{i_nj_n}, | ||
| + | $$ | ||
where the summation is over all possible partitions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072500/p07250013.png" /> of the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072500/p07250014.png" /> into non-intersecting pairs <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072500/p07250015.png" />, where one may suppose that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072500/p07250016.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072500/p07250017.png" />, and where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072500/p07250018.png" /> is the sign of the permutation | where the summation is over all possible partitions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072500/p07250013.png" /> of the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072500/p07250014.png" /> into non-intersecting pairs <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072500/p07250015.png" />, where one may suppose that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072500/p07250016.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072500/p07250017.png" />, and where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072500/p07250018.png" /> is the sign of the permutation | ||
Revision as of 14:09, 25 January 2012
of a skew-symmetric matrix $X$
The polynomial $\text{Pf } X$ in the entries of $X$ whose square is $\text{det } X$. More precisely, if $X = \|x_{ij}\|$ is a skew-symmetric matrix (i.e. $x_{ij}=-x_{ji}$, $x_{ii}=0$; such a matrix is sometimes also called an alternating matrix) of order $2n$ over a commutative-associative ring $A$ with a unit, then $\text{Pf } X$ is the element of $A$ given by the formula
$$ \text{Pf } X = \sum_s \varepsilon(s)x_{i_1j_1}\ldotsx_{i_nj_n}, $$
where the summation is over all possible partitions 
of the set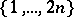 
into non-intersecting pairs 
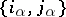, where one may suppose that 
, 
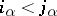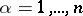, and where 
is the sign of the permutation
 |
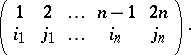A Pfaffian has the following properties:
1) 
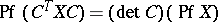for any matrix 
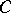of order 
;
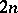2) 
;
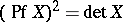3) if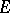 
is a free 
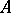-module with basis 
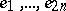and if
 |
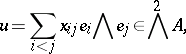then
 |
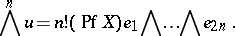References
| [1] | N. Bourbaki, "Elements of mathematics. Algebra: Modules. Rings. Forms" , 2 , Addison-Wesley (1975) pp. Chapt.4;5;6 (Translated from French) |
How to Cite This Entry:
Rafael.greenblatt/sandbox/Pfaffian. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rafael.greenblatt/sandbox/Pfaffian&oldid=20484
Rafael.greenblatt/sandbox/Pfaffian. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rafael.greenblatt/sandbox/Pfaffian&oldid=20484