Borel measure

of sets

[ 2010 Mathematics Subject Classification MSN: 28C15 | MSCwiki: 28C15  ]

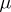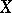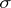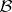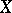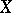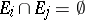A non-negative function of the subsets of a topological space possessing the following properties: 1) its domain of definition is the -algebra of Borel sets (cf. Borel set) in , i.e. the smallest class of subsets in containing the open sets and closed with respect to the set-theoretic operations performed a countable number of times; and 2) if when 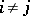, i.e. 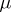is countably additive. A Borel measure 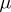is called regular if

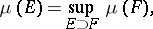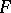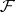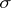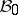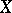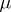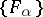where belongs to the class of closed subsets in . The study of Borel measures is often connected with that of Baire measures, which differ from Borel measures only in their domain of definition: They are defined on the smallest -algebra with respect to which all continuous functions on are measurable. A Borel measure (or a Baire measure ) is said to be -smooth if for any net of closed sets which satisfies the condition 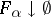(or 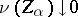for any net 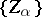of sets which are zero sets of continuous functions and such that 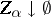). A Borel measure (or Baire measure ) is said to be tight if

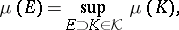where 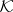is the class of compact subsets on 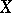(or

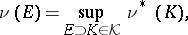where

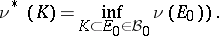Tightness and -smoothness are restrictions which ensure additional smoothness of measures, and which in fact often hold. Under certain conditions Baire measures can be extended to Borel measures. For instance, if 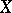is a completely-regular Hausdorff space, then any -smooth (tight) finite Baire measure can be extended to a regular -smooth (tight) finite Borel measure. In the study of measures on locally compact spaces Borel measures (or Baire measures) is the name sometimes given to measures defined on the 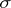-ring of sets generated by the compact (or 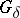-compact) sets and which are finite on compact sets. Often, by the Borel measure on the real line one understands the measure defined on the Borel sets such that its value on an arbitrary segment is equal to the length of that segment.

References

[1]	V.S. Varadarajan, "Measures on topological spaces" Transl. Amer. Math. Soc. Ser. 2 , 48 (1965) pp. 161–228 Mat. Sb. , 55 (97) : 1 (1961) pp. 35–100
[2]	P.R. Halmos, "Measure theory" , v. Nostrand (1950)
[3]	J. Neveu, "Bases mathématiques du calcul des probabilités" , Masson (1970)

References

[a1]	H.L. Royden, "Real analysis" , Macmillan (1968)
[a2]	A.C. Zaanen, "Integration" , North-Holland (1967)
[a3]	W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1953)
[a4]	W. Rudin, "Real and complex analysis" , McGraw-Hill (1966) pp. 98
[a5]	A.E. Taylor, "General theory of functions and integration" , Blaisdell (1965)
[a6]	C.D. Aliprantz, O. Burleinshaw, "Principles of real analysis" , North-Holland (1981)