Difference between revisions of "Covariant differential"
From Encyclopedia of Mathematics
(Importing text file) |
(TeX) |
||
| Line 1: | Line 1: | ||
| + | {{TEX|done}} | ||
A generalization of the notion of a differential to fields of different geometric objects. It is a tensor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026860/c0268601.png" />-form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026860/c0268602.png" /> on a manifold with values in the module of tensor fields <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026860/c0268603.png" /> defined by the formula | A generalization of the notion of a differential to fields of different geometric objects. It is a tensor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026860/c0268601.png" />-form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026860/c0268602.png" /> on a manifold with values in the module of tensor fields <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026860/c0268603.png" /> defined by the formula | ||
Revision as of 15:32, 10 August 2014
A generalization of the notion of a differential to fields of different geometric objects. It is a tensor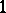 
-form 
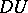on a manifold with values in the module of tensor fields 
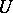defined by the formula
 |
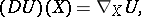where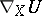 
is the covariant derivative of the field 
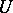along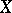 
. For detailed information, see Covariant differentiation.
How to Cite This Entry:
Covariant differential. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Covariant_differential&oldid=18963
Covariant differential. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Covariant_differential&oldid=18963
This article was adapted from an original article by I.Kh. Sabitov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article