Difference between revisions of "Periodic point"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 8: | Line 8: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian) {{MR|0121520}} {{ZBL|0089.29502}} </TD></TR></table> |
| Line 16: | Line 16: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> C. Conley, E. Zehnder, "Morse type index theory for flows and periodic solutions for Hamiltonian equations" ''Comm. Pure Appl. Math.'' , '''37''' (1984) pp. 207–253 {{MR|0733717}} {{ZBL|0559.58019}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> N.G. Lloyd, "Limit cycles of polynomial systems - some recent developments" T. Bedford (ed.) J. Swift (ed.) , ''New directions in dynamical systems'' , Cambridge Univ. Press (1988) pp. 192–234 {{MR|0953973}} {{ZBL|0646.34040}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> L. Markus, "Lectures in differentiable dynamics" , Amer. Math. Soc. (1980) pp. Appendix II {{MR|0309152}} {{ZBL|0214.50701}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> D.A. Neumann, "Existence of periodic orbits on 2-manifolds" ''J. Differential Eq.'' , '''27''' (1987) pp. 313–319 {{MR|0482857}} {{ZBL|0337.34041}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> P.H. Rabinowitz (ed.) A. Ambrosetti (ed.) I. Ekeland (ed.) E.J. Zehnder (ed.) , ''Periodic solutions of Hamiltonian systems and related topics'' , ''Proc. NATO Adv. Res. Workshop, 1986'' , Reidel (1987) {{MR|0920604}} {{ZBL|0621.00013}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> R.J. Sacker, G.R. Sell, "On the existence of periodic solutions on 2-manifolds" ''J. Differential Eq.'' , '''11''' (1972) pp. 449–463 {{MR|0298706}} {{ZBL|0242.34042}} </TD></TR></table> |
Revision as of 17:00, 15 April 2012
of a dynamical system
A point on a trajectory of a periodic motion of a dynamical system 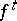 (
(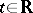 or
or 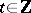 ) defined on a space
) defined on a space 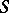 , i.e. a point
, i.e. a point 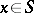 such that there is a number
such that there is a number 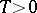 for which
for which  but
but  for
for 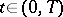 . This number
. This number 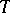 is called the period of the point
is called the period of the point  (sometimes, the name period is also given to all integer multiples of
(sometimes, the name period is also given to all integer multiples of 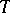 ).
).
The trajectory of a periodic point is called a closed trajectory or a loop. When the latter terms are used, one frequently abandons a concrete parametrization of the set of points on the trajectory with parameter 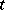 and considers some class of equivalent parametrizations: If
and considers some class of equivalent parametrizations: If 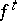 is a continuous action of the group
is a continuous action of the group 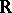 on a topological space
on a topological space 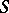 , a loop is considered as a circle that is topologically imbedded in
, a loop is considered as a circle that is topologically imbedded in 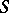 ; if
; if 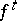 is a differentiable action of the group
is a differentiable action of the group 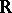 on a differentiable manifold
on a differentiable manifold  , a loop is considered as a circle that is smoothly imbedded in
, a loop is considered as a circle that is smoothly imbedded in 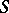 .
.
If  is a periodic point (and
is a periodic point (and  is a metric space), then the
is a metric space), then the 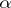 -limit set
-limit set  and the
and the 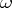 -limit set
-limit set 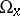 (cf. Limit set of a trajectory) coincide with its trajectory (as point sets). This property, to a certain extent, distinguishes a periodic point among all points that are not fixed, i.e. if the space in which the dynamical system
(cf. Limit set of a trajectory) coincide with its trajectory (as point sets). This property, to a certain extent, distinguishes a periodic point among all points that are not fixed, i.e. if the space in which the dynamical system  is given is a complete metric space and if a point
is given is a complete metric space and if a point  is such that
is such that 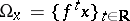 , then
, then  is a fixed or a periodic point of
is a fixed or a periodic point of  .
.
References
| [1] | V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian) MR0121520 Zbl 0089.29502 |
Comments
In arbitrary dynamical systems (where the phase space is not necessarily metric) the periodic points are characterized as follows (both for actions of 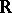 and of
and of 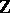 ): A point is periodic if and only if its trajectory is a compact set consisting of more than one point. The question whether a given dynamical system has periodic points has been much studied. For dynamical systems on
): A point is periodic if and only if its trajectory is a compact set consisting of more than one point. The question whether a given dynamical system has periodic points has been much studied. For dynamical systems on  -manifolds, see e.g. [a4], [a6] and also Limit cycle; Poincaré–Bendixson theory and Kneser theorem. For Hamiltonian systems (cf. Hamiltonian system) see e.g. [a5], and for Hilbert's 16th problem (i.e., what is the number of limit cycles of a polynomial vector field in the plane?) see [a2]. Well-known is the Seifert conjecture. Every
-manifolds, see e.g. [a4], [a6] and also Limit cycle; Poincaré–Bendixson theory and Kneser theorem. For Hamiltonian systems (cf. Hamiltonian system) see e.g. [a5], and for Hilbert's 16th problem (i.e., what is the number of limit cycles of a polynomial vector field in the plane?) see [a2]. Well-known is the Seifert conjecture. Every 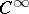 -dynamical system on
-dynamical system on  has a periodic trajectory; see e.g. [a3]. For a connection between (the existence of) periodic trajectories and certain topological invariants (cf. also Singular point, index of a), see e.g. [a1].
has a periodic trajectory; see e.g. [a3]. For a connection between (the existence of) periodic trajectories and certain topological invariants (cf. also Singular point, index of a), see e.g. [a1].
References
| [a1] | C. Conley, E. Zehnder, "Morse type index theory for flows and periodic solutions for Hamiltonian equations" Comm. Pure Appl. Math. , 37 (1984) pp. 207–253 MR0733717 Zbl 0559.58019 |
| [a2] | N.G. Lloyd, "Limit cycles of polynomial systems - some recent developments" T. Bedford (ed.) J. Swift (ed.) , New directions in dynamical systems , Cambridge Univ. Press (1988) pp. 192–234 MR0953973 Zbl 0646.34040 |
| [a3] | L. Markus, "Lectures in differentiable dynamics" , Amer. Math. Soc. (1980) pp. Appendix II MR0309152 Zbl 0214.50701 |
| [a4] | D.A. Neumann, "Existence of periodic orbits on 2-manifolds" J. Differential Eq. , 27 (1987) pp. 313–319 MR0482857 Zbl 0337.34041 |
| [a5] | P.H. Rabinowitz (ed.) A. Ambrosetti (ed.) I. Ekeland (ed.) E.J. Zehnder (ed.) , Periodic solutions of Hamiltonian systems and related topics , Proc. NATO Adv. Res. Workshop, 1986 , Reidel (1987) MR0920604 Zbl 0621.00013 |
| [a6] | R.J. Sacker, G.R. Sell, "On the existence of periodic solutions on 2-manifolds" J. Differential Eq. , 11 (1972) pp. 449–463 MR0298706 Zbl 0242.34042 |
Periodic point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Periodic_point&oldid=18768