Difference between revisions of "Machine learning"
(Importing text file) |
m (AUTOMATIC EDIT (latexlist): Replaced 63 formulas out of 65 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 65 formulas, 63 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|partial}} | ||
''ML'' | ''ML'' | ||
| − | Machine learning is concerned with modifying the knowledge representation structures (or knowledge base) underlying a computer program such that its problem-solving capability improves (for surveys, cf. [[#References|[a6]]], [[#References|[a2]]]). More specifically, a program is said to learn from experience | + | Machine learning is concerned with modifying the knowledge representation structures (or knowledge base) underlying a computer program such that its problem-solving capability improves (for surveys, cf. [[#References|[a6]]], [[#References|[a2]]]). More specifically, a program is said to learn from experience $E$ with respect to some class of tasks $T$ and performance measure $\pi$, if its performance at tasks $t \in T$, as measured by $\pi$, improves as training experience $E$ increases. |
Given this definition, any learning system must make choices along the following dimensions: | Given this definition, any learning system must make choices along the following dimensions: | ||
| Line 11: | Line 19: | ||
The kind of representation structure the learning system will use in order to describe the target function to be learned. The choice of that representation structure implies a direct correlation between expressiveness and the required size of the training data. | The kind of representation structure the learning system will use in order to describe the target function to be learned. The choice of that representation structure implies a direct correlation between expressiveness and the required size of the training data. | ||
| − | A learning algorithm which evaluates training examples in order to approximate effectively the target function by a learning hypothesis. Each training example is a pair composed of a training instance (a particular state in the problem space) and a corresponding value assignment. The latter is related to the utility of the training instance for properly solving the tasks | + | A learning algorithm which evaluates training examples in order to approximate effectively the target function by a learning hypothesis. Each training example is a pair composed of a training instance (a particular state in the problem space) and a corresponding value assignment. The latter is related to the utility of the training instance for properly solving the tasks $t \in T$. The validity ( "best fit" ) of the function approximation (on the training set) might be assessed by computing the minimum of the squared error between the training values and the values predicted by the learning hypothesis, given the particular training instance. |
| − | This approach to machine learning can be characterized as a form of inductive inference, where, from a sample of examples of a function | + | This approach to machine learning can be characterized as a form of inductive inference, where, from a sample of examples of a function $f$, a hypothesis function $\hat { f }$ is guessed that approximates $f$ as closely as possible. Alternatively, one may consider machine learning as a search problem (cf. [[Search algorithm|Search algorithm]]). This typically involves a very large (usually, exponentially growing) search space of possible target functions and requires to determine the one(s) which best fit(s) the data in terms of task accomplishment. |
A learning system can be viewed as consisting of four main components: | A learning system can be viewed as consisting of four main components: | ||
| − | the performance system solves the tasks | + | the performance system solves the tasks $t \in T$ by using the hypothesis, or learned target function, $\hat { f }$; |
| − | a critic, given a trace of each solution, judges the quality of the solution by comparing training instances with their benefits as computed by | + | a critic, given a trace of each solution, judges the quality of the solution by comparing training instances with their benefits as computed by $\hat { f }$; |
| − | the generalizer generalizes from this set of training examples in order to better fit the available and, possibly, additional data by hypothesizing a more general function, | + | the generalizer generalizes from this set of training examples in order to better fit the available and, possibly, additional data by hypothesizing a more general function, $\hat { f }^{\prime}$, according to the "best fit" criterion just discussed; and, finally, |
| − | the experiment generator takes this new hypothesis | + | the experiment generator takes this new hypothesis $\hat { f }^{\prime}$ and outputs a new task $t \in T$ to the performance system, thus closing the update loop. |
Machine learning is typically applied to tasks which involve the classification of new, unseen examples into one of a discrete set of possible categories. The inference of a corresponding target function, a so-called classifier, from training examples is often referred to as concept learning. If the target function involves the representation of "if-then" rules, this kind of learning is referred to as rule learning. If the learning involves sequences of actions and the task consists of acquiring a control strategy for choosing appropriate actions to achieve a goal, this mode is sometimes referred to as policy learning. | Machine learning is typically applied to tasks which involve the classification of new, unseen examples into one of a discrete set of possible categories. The inference of a corresponding target function, a so-called classifier, from training examples is often referred to as concept learning. If the target function involves the representation of "if-then" rules, this kind of learning is referred to as rule learning. If the learning involves sequences of actions and the task consists of acquiring a control strategy for choosing appropriate actions to achieve a goal, this mode is sometimes referred to as policy learning. | ||
| Line 33: | Line 41: | ||
2) Divide it into two disjoint sets: the training set and the test set. | 2) Divide it into two disjoint sets: the training set and the test set. | ||
| − | 3) Run the learning algorithm with exemplars only taken from the training set and generate an approximation of the target function, the learning hypothesis | + | 3) Run the learning algorithm with exemplars only taken from the training set and generate an approximation of the target function, the learning hypothesis $\hat { f }$. |
| − | 4) Evaluate the degree of correct classifications of the current version of | + | 4) Evaluate the degree of correct classifications of the current version of $\hat { f }$ and update it to reduce the number of misclassifications. |
5) Repeat steps 2)–4) for different randomly selected training sets of various sizes, until the learning algorithm delivers a sufficient degree of correct classifications. | 5) Repeat steps 2)–4) for different randomly selected training sets of various sizes, until the learning algorithm delivers a sufficient degree of correct classifications. | ||
| Line 43: | Line 51: | ||
A crucial issue for machine learning is the kind of representation structure underlying the target function. The representation formalisms most widely used are attribute-value pairs, first-order predicate logic, neural networks, and probabilistic functions. | A crucial issue for machine learning is the kind of representation structure underlying the target function. The representation formalisms most widely used are attribute-value pairs, first-order predicate logic, neural networks, and probabilistic functions. | ||
| − | Attribute-value representations address Boolean functions which deal with different logical combinations of attribute-value pairs (a single attribute may have continuous or discrete values, discrete ones can be Boolean or multi-valued; cf. also [[Boolean function|Boolean function]]). More specifically, one assumes given some finite hypothesis space | + | Attribute-value representations address Boolean functions which deal with different logical combinations of attribute-value pairs (a single attribute may have continuous or discrete values, discrete ones can be Boolean or multi-valued; cf. also [[Boolean function|Boolean function]]). More specifically, one assumes given some finite hypothesis space $\mathcal{H}$ defined over the instance space $\mathcal{X}$, in which the task is to learn some target function (target concept or classifier) $c : \mathcal X \rightarrow \{ 0,1 \}$. The learner is given a sequence of training examples $\{ \langle x _ { 1 } , d _ { 1 } \rangle , \ldots , \langle x _ { n } , d _ { n } \rangle \}$, where $x _ { i } \in \cal X$ and $d _ { i } = c ( x _ { i } )$. Now, $\hat { f } \in \mathcal{H}$, the learning hypothesis, is supposed to approximate $c$ such that $\hat { f } ( x _ { i } ) = c ( x _ { i } )$ for the vast majority (ideally, all) of the cases, and $\widehat { f } ( x _ { i } ) \neq c ( x _ { i } )$ for only few (ideally, no) cases, certainly not exceeding a given minimum bound. |
Decision trees [[#References|[a8]]] are the most commonly used attribute-value representation. Given an exemplar described by a set of attribute values (or a feature vector), a decision tree outputs a Boolean classification decision for that exemplar. The decision is reached by branching through the node structure of the decision tree. Each of its nodes tests the value of one of the attributes and branches to one of its children, depending on the outcome of the test. Hence, a decision tree implements the learned target function. | Decision trees [[#References|[a8]]] are the most commonly used attribute-value representation. Given an exemplar described by a set of attribute values (or a feature vector), a decision tree outputs a Boolean classification decision for that exemplar. The decision is reached by branching through the node structure of the decision tree. Each of its nodes tests the value of one of the attributes and branches to one of its children, depending on the outcome of the test. Hence, a decision tree implements the learned target function. | ||
| Line 53: | Line 61: | ||
Probabilistic functions return a probability distribution over a set of propositional (or multi-valued) random variables (possible output values), and are suitable for problems where there may be uncertainty as to the correct answer (cf. [[Probability theory|Probability theory]]). They calculate the probability distribution for the unknown variables, given observed values for the remaining variables based on the [[Bayes formula|Bayes formula]]. | Probabilistic functions return a probability distribution over a set of propositional (or multi-valued) random variables (possible output values), and are suitable for problems where there may be uncertainty as to the correct answer (cf. [[Probability theory|Probability theory]]). They calculate the probability distribution for the unknown variables, given observed values for the remaining variables based on the [[Bayes formula|Bayes formula]]. | ||
| − | In machine learning, two basic uses of Bayes' theorem can be distinguished. In the first approach, the naïve Bayesian classifier, a new instance, described by a tuple of attribute values | + | In machine learning, two basic uses of Bayes' theorem can be distinguished. In the first approach, the naïve Bayesian classifier, a new instance, described by a tuple of attribute values $\langle a _ { 1 } , \dots , a _ { n } \rangle$, is classified by assigning the most probable target value, taken from some finite set $\mathcal{V}$, the so-called maximum a posteriori hypothesis, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130010/m13001031.png"/>. Using Bayes' theorem one may state |
| − | + | \begin{equation} \tag{a1} v _ { \operatorname {MAP} } = \operatorname { arg } \operatorname { max } _ { v _ { j } \in \mathcal{V} } \mathsf{P} ( a _ { 1 } , \ldots , a _ { n } | v _ { j } ) \cdot \mathsf{P} ( v _ { j } ). \end{equation} | |
Incorporating the simplifying assumption that the attribute values are conditionally independent given the target value (cf. also [[Conditional distribution|Conditional distribution]]), one may rewrite (a1) as | Incorporating the simplifying assumption that the attribute values are conditionally independent given the target value (cf. also [[Conditional distribution|Conditional distribution]]), one may rewrite (a1) as | ||
| − | + | \begin{equation} \tag{a2} v _ { \operatorname {MAP} } = \operatorname { arg } \operatorname { max } _ { v _ { j } \in \mathcal{V} } \prod _ { i } \mathsf{P} ( a _ { i } | v _ { j } ) \cdot \mathsf{P} ( v _ { j } ) . \end{equation} | |
| − | In contrast to the naïve Bayesian classifier, which assumes that all the variables are conditionally independent given the target value, Bayesian networks allow stating conditional independence assumptions that apply to subsets of the variables. In particular, a node in a Bayesian network corresponds to a single random variable | + | In contrast to the naïve Bayesian classifier, which assumes that all the variables are conditionally independent given the target value, Bayesian networks allow stating conditional independence assumptions that apply to subsets of the variables. In particular, a node in a Bayesian network corresponds to a single random variable $X_i$, and a link between two nodes represents the causal dependency between the parent and the child node. The strength of the causal relation is represented by the conditional probability $\mathsf{P} ( X _ { i } | \gamma _ { i } )$ of each possible value of the variable, given each possible combination of values of the parent nodes ($\gamma _ { i }$ being the set of predecessors of $X_i$). |
The problem that is posed by the appropriate choice of the underlying representation formalism is, as with formal reasoning, the fundamental trade-off between expressiveness (is the desired function representable in the chosen representation format?) and efficiency (is the machine learning problem tractable for the given choice of the representation format?). | The problem that is posed by the appropriate choice of the underlying representation formalism is, as with formal reasoning, the fundamental trade-off between expressiveness (is the desired function representable in the chosen representation format?) and efficiency (is the machine learning problem tractable for the given choice of the representation format?). | ||
| Line 69: | Line 77: | ||
Inductive learning is typically seen as supervised learning, where the learning problem is formulated as one to predict the output of a function from its input, given a collection of examples with a priori known inputs and outputs. With unsupervised learning such correctly labelled training exemplars are not available. Instead the learning system receives some sort of continuous reward indicating whether it was successful or whether it failed, an approach which underlies a variety of reinforcement learning algorithms [[#References|[a11]]]. | Inductive learning is typically seen as supervised learning, where the learning problem is formulated as one to predict the output of a function from its input, given a collection of examples with a priori known inputs and outputs. With unsupervised learning such correctly labelled training exemplars are not available. Instead the learning system receives some sort of continuous reward indicating whether it was successful or whether it failed, an approach which underlies a variety of reinforcement learning algorithms [[#References|[a11]]]. | ||
| − | From a technical perspective, in reinforcement learning, environments are usually treated as being in one of a set of discrete states | + | From a technical perspective, in reinforcement learning, environments are usually treated as being in one of a set of discrete states $S$. Actions cause transitions between states. Hence, a complete model of an environment specifies the probability that the environment will be in state $j \in S$ if action $a$ is executed in state $i \in S$. This probability is denoted by $M _ { i j }^a$. Furthermore, a reward $R ( i )$ is associated with each state $i$. Together, $M$ and $R$ specify a Markov decision process (cf. [[Markov process|Markov process]]). Its ideal behaviour maximizes the expected total reward until a terminal state is reached. |
One may also draw a distinction between learning based on pure induction and other inference modes for learning that take only few examples, sometimes even only a single example. One of these approaches is based on analogical reasoning. This is an inference process in which the similarity between a source and a target is inferred from the presence of known similarities, thereby providing new information about the target when that information is known about the source. One may provide syntactic measures of the amount of known similarity to assess the suitability of a given source (similarity-based analogy), or use prior knowledge of the relevance of one property to another to generate sound analogical inferences (relevance-based analogy) [[#References|[a9]]]. | One may also draw a distinction between learning based on pure induction and other inference modes for learning that take only few examples, sometimes even only a single example. One of these approaches is based on analogical reasoning. This is an inference process in which the similarity between a source and a target is inferred from the presence of known similarities, thereby providing new information about the target when that information is known about the source. One may provide syntactic measures of the amount of known similarity to assess the suitability of a given source (similarity-based analogy), or use prior knowledge of the relevance of one property to another to generate sound analogical inferences (relevance-based analogy) [[#References|[a9]]]. | ||
| Line 79: | Line 87: | ||
The basic idea behind computational learning theory (or PAC learning) [[#References|[a4]]] is the assumption that a hypothesis which is fundamentally wrong will almost certainly be identified with high probability after it has been exposed to only a few examples, simply because it makes wrong predictions. Thus, any hypothesis that is consistent with a sufficiently large set of training examples is unlikely to be seriously wrong, i.e., it must be "probably approximately correct" (PAC). | The basic idea behind computational learning theory (or PAC learning) [[#References|[a4]]] is the assumption that a hypothesis which is fundamentally wrong will almost certainly be identified with high probability after it has been exposed to only a few examples, simply because it makes wrong predictions. Thus, any hypothesis that is consistent with a sufficiently large set of training examples is unlikely to be seriously wrong, i.e., it must be "probably approximately correct" (PAC). | ||
| − | More specifically, assume an unknown distribution or density | + | More specifically, assume an unknown distribution or density $P$ over an instance space $\mathcal{X}$, and an unknown Boolean target function $f$ over $\mathcal{X}$, chosen from a known class $\mathcal{F}$ of such functions. The finite sample given to the learning algorithm consists of pairs $\{ \langle x _ { 1 } , y _ { 1 } \rangle , \dots , \langle x _ { m } , y _ { m } \rangle \}$, where $x_{i}$ is distributed according to $P$ and $y _ { i } = f ( x _ { i } )$. Let $\mathcal{F}$ be the class of all linear-threshold functions (perceptrons) over $n$-dimensional real inputs. The question arises whether there is a learning algorithm that, for any input dimension $n$ and any desired error $\epsilon > 0$, requires a sample size and execution time bounded by fixed polynomials in $n$ and $1 / \epsilon$, and produces, with high probability, a hypothesis function $h$ such that the probability that $h ( x _ { i } ) \neq f ( x _ { i } )$ is smaller than <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130010/m13001064.png"/> under $P$. One interesting result in that theory shows that the pure inductive learning problem, where the learning system begins with no prior knowledge about the target function, is computationally infeasible in the worst case. |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> "Backpropagation: Theory, architectures and applications" Y. Chauvin (ed.) D.E. Rumelhart (ed.) , Lawrence Erlbaum (1993)</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> S. Weiss, C. Kulikowski, "Computer systems that learn. Classification and prediction methods from statistics, neural nets, machine learning and expert systems" , Kaufmann (1991)</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> T. Ellman, "Explanation-based learning: A survey of programs and perspectives" ''ACM Computing Surveys'' , '''21''' : 2 (1989) pp. 163–221</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> M. Kearns, U. Vazirani, "An introduction to computational learning theory" , MIT (1994)</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> M. Li, P. Vitanyi, "An introduction to Kolmogorov complexity and its applications" , Springer (1993)</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> T. Mitchell, "Machine learning" , McGraw-Hill (1997)</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> S. Muggleton, "Foundations of inductive logic programming" , Prentice-Hall (1995)</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> J.R. Quinlan, "C4.5: Programs for machine learning" , Kaufmann (1993)</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> S.J. Russell, "The use of knowledge in analogy and induction" , Pitman (1989)</td></tr><tr><td valign="top">[a10]</td> <td valign="top"> J. Shrager, P. Langley, "Computational models of scientific discovery and theory formation" , Kaufmann (1990)</td></tr><tr><td valign="top">[a11]</td> <td valign="top"> R.S. Sutton, A.G. Barto, "Reinforcement learning. An introduction" , MIT (1998)</td></tr></table> |
Revision as of 16:59, 1 July 2020
ML
Machine learning is concerned with modifying the knowledge representation structures (or knowledge base) underlying a computer program such that its problem-solving capability improves (for surveys, cf. [a6], [a2]). More specifically, a program is said to learn from experience $E$ with respect to some class of tasks $T$ and performance measure $\pi$, if its performance at tasks $t \in T$, as measured by $\pi$, improves as training experience $E$ increases.
Given this definition, any learning system must make choices along the following dimensions:
The type of training experience from which the system will learn, so that it may either directly or, worse, indirectly assess whether its performance on certain tasks has improved.
The type of knowledge which the system will learn, its target function, and how that knowledge will be used after the training phase. Care has to be taken that this function contains an operational description such that it be efficiently computable and properly approximates the "ideal" target function.
The kind of representation structure the learning system will use in order to describe the target function to be learned. The choice of that representation structure implies a direct correlation between expressiveness and the required size of the training data.
A learning algorithm which evaluates training examples in order to approximate effectively the target function by a learning hypothesis. Each training example is a pair composed of a training instance (a particular state in the problem space) and a corresponding value assignment. The latter is related to the utility of the training instance for properly solving the tasks $t \in T$. The validity ( "best fit" ) of the function approximation (on the training set) might be assessed by computing the minimum of the squared error between the training values and the values predicted by the learning hypothesis, given the particular training instance.
This approach to machine learning can be characterized as a form of inductive inference, where, from a sample of examples of a function $f$, a hypothesis function $\hat { f }$ is guessed that approximates $f$ as closely as possible. Alternatively, one may consider machine learning as a search problem (cf. Search algorithm). This typically involves a very large (usually, exponentially growing) search space of possible target functions and requires to determine the one(s) which best fit(s) the data in terms of task accomplishment.
A learning system can be viewed as consisting of four main components:
the performance system solves the tasks $t \in T$ by using the hypothesis, or learned target function, $\hat { f }$;
a critic, given a trace of each solution, judges the quality of the solution by comparing training instances with their benefits as computed by $\hat { f }$;
the generalizer generalizes from this set of training examples in order to better fit the available and, possibly, additional data by hypothesizing a more general function, $\hat { f }^{\prime}$, according to the "best fit" criterion just discussed; and, finally,
the experiment generator takes this new hypothesis $\hat { f }^{\prime}$ and outputs a new task $t \in T$ to the performance system, thus closing the update loop.
Machine learning is typically applied to tasks which involve the classification of new, unseen examples into one of a discrete set of possible categories. The inference of a corresponding target function, a so-called classifier, from training examples is often referred to as concept learning. If the target function involves the representation of "if-then" rules, this kind of learning is referred to as rule learning. If the learning involves sequences of actions and the task consists of acquiring a control strategy for choosing appropriate actions to achieve a goal, this mode is sometimes referred to as policy learning.
A particular learning algorithm is as good or as bad as its performance is on classifying unseen exemplars, i.e., whether its decisions are right or wrong. A methodology for checking the prediction quality of a learning algorithm involves the following steps:
1) Collect a large set of examples.
2) Divide it into two disjoint sets: the training set and the test set.
3) Run the learning algorithm with exemplars only taken from the training set and generate an approximation of the target function, the learning hypothesis $\hat { f }$.
4) Evaluate the degree of correct classifications of the current version of $\hat { f }$ and update it to reduce the number of misclassifications.
5) Repeat steps 2)–4) for different randomly selected training sets of various sizes, until the learning algorithm delivers a sufficient degree of correct classifications.
Inherent to the choice of a large set of examples and the approximation of the target function are several well-known problems. These include, among others, noise in the data (e.g., when two examples have the same description but are assigned different a priori classification categories), and over-fitting of the learned target function in the sense that it does well for the training set but fails for the test set (mostly due to incorporating irrelevant attributes in the target function).
A crucial issue for machine learning is the kind of representation structure underlying the target function. The representation formalisms most widely used are attribute-value pairs, first-order predicate logic, neural networks, and probabilistic functions.
Attribute-value representations address Boolean functions which deal with different logical combinations of attribute-value pairs (a single attribute may have continuous or discrete values, discrete ones can be Boolean or multi-valued; cf. also Boolean function). More specifically, one assumes given some finite hypothesis space $\mathcal{H}$ defined over the instance space $\mathcal{X}$, in which the task is to learn some target function (target concept or classifier) $c : \mathcal X \rightarrow \{ 0,1 \}$. The learner is given a sequence of training examples $\{ \langle x _ { 1 } , d _ { 1 } \rangle , \ldots , \langle x _ { n } , d _ { n } \rangle \}$, where $x _ { i } \in \cal X$ and $d _ { i } = c ( x _ { i } )$. Now, $\hat { f } \in \mathcal{H}$, the learning hypothesis, is supposed to approximate $c$ such that $\hat { f } ( x _ { i } ) = c ( x _ { i } )$ for the vast majority (ideally, all) of the cases, and $\widehat { f } ( x _ { i } ) \neq c ( x _ { i } )$ for only few (ideally, no) cases, certainly not exceeding a given minimum bound.
Decision trees [a8] are the most commonly used attribute-value representation. Given an exemplar described by a set of attribute values (or a feature vector), a decision tree outputs a Boolean classification decision for that exemplar. The decision is reached by branching through the node structure of the decision tree. Each of its nodes tests the value of one of the attributes and branches to one of its children, depending on the outcome of the test. Hence, a decision tree implements the learned target function.
First-order predicate logic (cf. Predicate calculus) is certainly the most powerful representation language currently (2000) considered within the machine-learning community, though the one which requires the most sophisticated training environment and most costly computations to determine the target function. For example, inductive logic programming (ILP) [a7] combines inductive reasoning and first-order logical representations such that the representation language of target functions is considered as a logic program, i.e., a set of Horn clauses (cf. Logic programming). Inductive logic programming achieves inductive reasoning either by inverting resolution-based proofs or by performing a general-to-specific, hill-climbing search which starts with the most general preconditions possible, and adds literals, one at a time, to specialize the rule until it avoids all negative examples.
Neural networks are continuous, non-linear functions represented by a parametrized network of simple computing elements (cf. Neural network). The backpropagation algorithm [a1] for learning neural networks begins with an initial neural network with randomized weights and computes the classification error of that network on the training data. Subsequently, small adjustments in the weights of the network are carried out (by propagating classification errors backward through the network) in order to reduce the error. This process is repeated until the error reaches a certain minimum.
Probabilistic functions return a probability distribution over a set of propositional (or multi-valued) random variables (possible output values), and are suitable for problems where there may be uncertainty as to the correct answer (cf. Probability theory). They calculate the probability distribution for the unknown variables, given observed values for the remaining variables based on the Bayes formula.
In machine learning, two basic uses of Bayes' theorem can be distinguished. In the first approach, the naïve Bayesian classifier, a new instance, described by a tuple of attribute values $\langle a _ { 1 } , \dots , a _ { n } \rangle$, is classified by assigning the most probable target value, taken from some finite set $\mathcal{V}$, the so-called maximum a posteriori hypothesis, 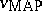 . Using Bayes' theorem one may state
. Using Bayes' theorem one may state
\begin{equation} \tag{a1} v _ { \operatorname {MAP} } = \operatorname { arg } \operatorname { max } _ { v _ { j } \in \mathcal{V} } \mathsf{P} ( a _ { 1 } , \ldots , a _ { n } | v _ { j } ) \cdot \mathsf{P} ( v _ { j } ). \end{equation}
Incorporating the simplifying assumption that the attribute values are conditionally independent given the target value (cf. also Conditional distribution), one may rewrite (a1) as
\begin{equation} \tag{a2} v _ { \operatorname {MAP} } = \operatorname { arg } \operatorname { max } _ { v _ { j } \in \mathcal{V} } \prod _ { i } \mathsf{P} ( a _ { i } | v _ { j } ) \cdot \mathsf{P} ( v _ { j } ) . \end{equation}
In contrast to the naïve Bayesian classifier, which assumes that all the variables are conditionally independent given the target value, Bayesian networks allow stating conditional independence assumptions that apply to subsets of the variables. In particular, a node in a Bayesian network corresponds to a single random variable $X_i$, and a link between two nodes represents the causal dependency between the parent and the child node. The strength of the causal relation is represented by the conditional probability $\mathsf{P} ( X _ { i } | \gamma _ { i } )$ of each possible value of the variable, given each possible combination of values of the parent nodes ($\gamma _ { i }$ being the set of predecessors of $X_i$).
The problem that is posed by the appropriate choice of the underlying representation formalism is, as with formal reasoning, the fundamental trade-off between expressiveness (is the desired function representable in the chosen representation format?) and efficiency (is the machine learning problem tractable for the given choice of the representation format?).
Machine learning as considered from the inductive perspective generates hypotheses by using combinations of existing terms in their vocabularies. These can, however, become rather clumsy and unintelligible. The problem may be overcome by introducing new terms into the vocabulary. In the machine learning community such systems are known as constructive induction or discovery systems [a10]. Basically, these systems employ techniques from inductive logic programming (such as constructive induction), or are concept formation systems, which generate definitions for new categories (usually attribute-based descriptions) in order to improve the classification of examples based on clustering algorithms.
Inductive learning is typically seen as supervised learning, where the learning problem is formulated as one to predict the output of a function from its input, given a collection of examples with a priori known inputs and outputs. With unsupervised learning such correctly labelled training exemplars are not available. Instead the learning system receives some sort of continuous reward indicating whether it was successful or whether it failed, an approach which underlies a variety of reinforcement learning algorithms [a11].
From a technical perspective, in reinforcement learning, environments are usually treated as being in one of a set of discrete states $S$. Actions cause transitions between states. Hence, a complete model of an environment specifies the probability that the environment will be in state $j \in S$ if action $a$ is executed in state $i \in S$. This probability is denoted by $M _ { i j }^a$. Furthermore, a reward $R ( i )$ is associated with each state $i$. Together, $M$ and $R$ specify a Markov decision process (cf. Markov process). Its ideal behaviour maximizes the expected total reward until a terminal state is reached.
One may also draw a distinction between learning based on pure induction and other inference modes for learning that take only few examples, sometimes even only a single example. One of these approaches is based on analogical reasoning. This is an inference process in which the similarity between a source and a target is inferred from the presence of known similarities, thereby providing new information about the target when that information is known about the source. One may provide syntactic measures of the amount of known similarity to assess the suitability of a given source (similarity-based analogy), or use prior knowledge of the relevance of one property to another to generate sound analogical inferences (relevance-based analogy) [a9].
The increasing reliance on some form of a priori knowledge is most evident in explanation-based learning (EBL) [a3]. It can be viewed as a form of single-instance generalization and uses background knowledge to construct an explanation of the observed learning exemplar, from which a generalization can be constructed. An important aspect of this approach to machine learning is that the general rule follows logically (or at least approximately so) from the background knowledge available to the learning system. Hence, it is based on deduction rather than induction. For explanation-based learning, the learning system does not actually learn anything substantially new from the observation, since the background knowledge must already be rich enough to explain the general rule, which in turn must explain the observation (often this approach, in contrast to inductive learning, is referred to as analytical learning). With the "new" piece of knowledge compiled-out, the system will, in the future, operate more efficiently rather than more effectively (hence, it can be considered as a form of speedup learning). Unlike inductive logic programming, another knowledge-intensive learning method, explanation-based learning does not extend the deductive closure of the knowledge structures already available to the learning system. This approach can also be viewed at as a third variant of analogy-based learning, viz. a kind of derivational analogy which uses knowledge of how the inferred similarities are derived from the known similarities to speed up analogical problem solving.
So far, machine learning has been discussed in terms of different approaches which aim at improving the performance of the learning system. One might also raise more principal questions as to the fundamental notions guiding research in machine learning or its theoretical limits. The notion of simplicity, for instance, is a primary one in induction, since a simple hypothesis that explains a large number of different examples seems to have captured some fundamental regularity in the underlying data. An influential formalization of the notion of simplicity (known as Kolmogorov complexity or minimum description length theory [a5]) considers a learning hypothesis as a program of a universal Turing machine (cf. Turing machine), with observations viewed as output from the execution of the program. The best hypothesis is the shortest program for the universal Turing machine that produces the observations as output (finding the shortest program is, however, an undecidable problem, cf. also Undecidability). This approach abstracts away from different configurations of universal Turing machines, since any universal Turing machine can encode any other with a program of finite length. Hence, although there are many different universal Turing machines, each of which might have a different shortest program, this can make a difference of at most a constant amount in the length of the shortest program.
The basic idea behind computational learning theory (or PAC learning) [a4] is the assumption that a hypothesis which is fundamentally wrong will almost certainly be identified with high probability after it has been exposed to only a few examples, simply because it makes wrong predictions. Thus, any hypothesis that is consistent with a sufficiently large set of training examples is unlikely to be seriously wrong, i.e., it must be "probably approximately correct" (PAC).
More specifically, assume an unknown distribution or density $P$ over an instance space $\mathcal{X}$, and an unknown Boolean target function $f$ over $\mathcal{X}$, chosen from a known class $\mathcal{F}$ of such functions. The finite sample given to the learning algorithm consists of pairs $\{ \langle x _ { 1 } , y _ { 1 } \rangle , \dots , \langle x _ { m } , y _ { m } \rangle \}$, where $x_{i}$ is distributed according to $P$ and $y _ { i } = f ( x _ { i } )$. Let $\mathcal{F}$ be the class of all linear-threshold functions (perceptrons) over $n$-dimensional real inputs. The question arises whether there is a learning algorithm that, for any input dimension $n$ and any desired error $\epsilon > 0$, requires a sample size and execution time bounded by fixed polynomials in $n$ and $1 / \epsilon$, and produces, with high probability, a hypothesis function $h$ such that the probability that $h ( x _ { i } ) \neq f ( x _ { i } )$ is smaller than  under $P$. One interesting result in that theory shows that the pure inductive learning problem, where the learning system begins with no prior knowledge about the target function, is computationally infeasible in the worst case.
under $P$. One interesting result in that theory shows that the pure inductive learning problem, where the learning system begins with no prior knowledge about the target function, is computationally infeasible in the worst case.
References
| [a1] | "Backpropagation: Theory, architectures and applications" Y. Chauvin (ed.) D.E. Rumelhart (ed.) , Lawrence Erlbaum (1993) |
| [a2] | S. Weiss, C. Kulikowski, "Computer systems that learn. Classification and prediction methods from statistics, neural nets, machine learning and expert systems" , Kaufmann (1991) |
| [a3] | T. Ellman, "Explanation-based learning: A survey of programs and perspectives" ACM Computing Surveys , 21 : 2 (1989) pp. 163–221 |
| [a4] | M. Kearns, U. Vazirani, "An introduction to computational learning theory" , MIT (1994) |
| [a5] | M. Li, P. Vitanyi, "An introduction to Kolmogorov complexity and its applications" , Springer (1993) |
| [a6] | T. Mitchell, "Machine learning" , McGraw-Hill (1997) |
| [a7] | S. Muggleton, "Foundations of inductive logic programming" , Prentice-Hall (1995) |
| [a8] | J.R. Quinlan, "C4.5: Programs for machine learning" , Kaufmann (1993) |
| [a9] | S.J. Russell, "The use of knowledge in analogy and induction" , Pitman (1989) |
| [a10] | J. Shrager, P. Langley, "Computational models of scientific discovery and theory formation" , Kaufmann (1990) |
| [a11] | R.S. Sutton, A.G. Barto, "Reinforcement learning. An introduction" , MIT (1998) |
Machine learning. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Machine_learning&oldid=18100