Kervaire-Milnor invariant

An invariant of framed surgery of a closed 6- or -dimensional framed manifold.

Let 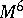be a stably-parallelizable -connected manifold on which is given a stable 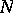-dimensional framing , i.e. a trivialization of the stable 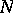-dimensional normal bundle. Let 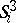be spheres realizing a basis of the -dimensional homology space of 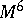. By summing the given 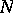-trivialization 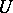with certain trivializations 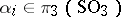of tubular neighbourhoods of the spheres 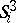in 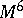, one obtains an 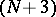-dimensional trivialization of the stable normal bundles to the spheres and the corresponding elements 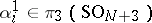. 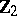The cokernel of the stable homomorphism is isomorphic to for 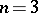, so that each sphere is put into correspondence with an element of the group 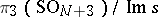(according to the value of the elements 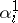which they take in the group 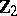after factorization by 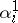). This value does not depend on the choice of the elements 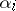, but depends only on the homology classes realized by the spheres 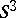and the framing 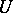. The Arf-invariant of the function 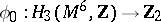so obtained satisfies the formula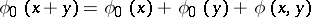 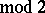, where 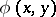is the intersection form of the -dimensional homology space on the manifold 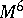, and is called the Kervaire–Milnor invariant of this manifold with framing 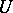. The pair has a framed surgery to the pair 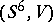if and only if the Kervaire–Milnor invariant of is zero.

Similar constructions have been carried out for . The Kervaire–Milnor invariant in dimension six is the only invariant of the stable 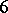-dimensional framed cobordism and defines an isomorphism 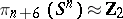, 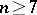. However, in dimension fourteen it is not a unique invariant of the stable 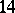-dimensional framed cobordism, i.e. the stable group 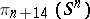, , 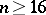is defined by framings on the sphere 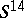and on .

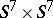For references see Kervaire invariant.