Difference between revisions of "Boolean functions, minimization of"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 23: | Line 23: | ||
are equivalent, the problem of minimization of Boolean functions is equivalent to the search for coverings with a minimal sum of the ranks of their intervals. Such coverings are called minimal. An interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696031.png" /> is called maximal for a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696032.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696033.png" /> and if there is no interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696034.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696035.png" />. The construction of dead-end disjunctive normal forms of a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696036.png" /> reduces to a search for coverings of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696037.png" /> by maximal intervals such that no proper subset of it is a covering of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696038.png" />. These coverings correspond to dead-end disjunctive normal forms and are called irreducible. They are obtained from coverings corresponding to abridged disjunctive normal forms by removal of certain intervals. | are equivalent, the problem of minimization of Boolean functions is equivalent to the search for coverings with a minimal sum of the ranks of their intervals. Such coverings are called minimal. An interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696031.png" /> is called maximal for a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696032.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696033.png" /> and if there is no interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696034.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696035.png" />. The construction of dead-end disjunctive normal forms of a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696036.png" /> reduces to a search for coverings of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696037.png" /> by maximal intervals such that no proper subset of it is a covering of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696038.png" />. These coverings correspond to dead-end disjunctive normal forms and are called irreducible. They are obtained from coverings corresponding to abridged disjunctive normal forms by removal of certain intervals. | ||
| − | The selection of the minimal disjunctive normal forms from all dead-end disjunctive normal forms is also a very laborious process, since | + | The selection of the minimal disjunctive normal forms from all dead-end disjunctive normal forms is also a very laborious process, since "almost-all" Boolean functions in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696039.png" /> arguments have no fewer than <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696040.png" /> different dead-end disjunctive normal forms. The diversity of the complexities of dead-end disjunctive normal forms may be very wide, so that if a random rather than a dead-end minimal disjunctive normal form is selected, a large error may result. |
Estimates of the number of dead-end disjunctive normal forms and of the scatter of their complexities show that a more detailed inspection during the elimination of the elementary conjunctions from a disjunctive normal form is a natural way of improving the effectiveness of minimization algorithms. A conjunction should be eliminated (or, on the contrary, retained until the end of the process) only if it can be established by some procedure that it does not occur in any minimal disjunctive normal form for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696041.png" /> (occurs in all minimal disjunctive normal forms for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696042.png" />). The latter fact is usually established by an analysis of the conjunctions that are close to the one in question, i.e. occur in a neighbourhood of it (cf. [[Algorithm, local|Algorithm, local]]). Here one has to accumulate information about elementary conjunctions and use it in the subsequent analysis. Procedures of this kind are known as local simplification algorithms. Some of them are quoted below, and their description involves the concept of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696044.png" />-th order neighbourhood <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696045.png" /> of an elementary conjunction <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696046.png" /> in a disjunctive normal form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696047.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696048.png" />. | Estimates of the number of dead-end disjunctive normal forms and of the scatter of their complexities show that a more detailed inspection during the elimination of the elementary conjunctions from a disjunctive normal form is a natural way of improving the effectiveness of minimization algorithms. A conjunction should be eliminated (or, on the contrary, retained until the end of the process) only if it can be established by some procedure that it does not occur in any minimal disjunctive normal form for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696041.png" /> (occurs in all minimal disjunctive normal forms for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696042.png" />). The latter fact is usually established by an analysis of the conjunctions that are close to the one in question, i.e. occur in a neighbourhood of it (cf. [[Algorithm, local|Algorithm, local]]). Here one has to accumulate information about elementary conjunctions and use it in the subsequent analysis. Procedures of this kind are known as local simplification algorithms. Some of them are quoted below, and their description involves the concept of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696044.png" />-th order neighbourhood <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696045.png" /> of an elementary conjunction <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696046.png" /> in a disjunctive normal form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696047.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696048.png" />. | ||
| Line 31: | Line 31: | ||
Quine's algorithm. Here one considers at each step the neighbourhood <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696062.png" /> of one of the conjunctions in the disjunctive normal form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696063.png" />. As the algorithm is executed for each conjunction, one attempts to compute one of the following properties: | Quine's algorithm. Here one considers at each step the neighbourhood <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696062.png" /> of one of the conjunctions in the disjunctive normal form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696063.png" />. As the algorithm is executed for each conjunction, one attempts to compute one of the following properties: | ||
| − | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696064.png" /> — | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696064.png" /> — "A occurs in all minimal disjunctive normal forms" ; and |
| − | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696065.png" /> — | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696065.png" /> — "A does not occur in any minimal disjunctive normal form" . |
The algorithm works as follows. 1) The neighbourhood <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696066.png" /> is successively formed for each conjunction <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696067.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696068.png" />. The inclusion <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696069.png" /> is verified. If this is not the case, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696070.png" /> is marked in some way as belonging to all minimal disjunctive normal forms. One says that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696071.png" /> is part of the kernel of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696072.png" /> (is a kernel conjunction). 2) Let the conjunctions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696073.png" /> be marked in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696074.png" /> in the first stage. The remaining conjunctions in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696075.png" /> are ordered, and the inclusion <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696076.png" /> is checked for each such conjunction <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696077.png" />. Conjunctions satisfying this relation do not occur in any minimal disjunctive normal form and are removed from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696078.png" />. | The algorithm works as follows. 1) The neighbourhood <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696066.png" /> is successively formed for each conjunction <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696067.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696068.png" />. The inclusion <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696069.png" /> is verified. If this is not the case, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696070.png" /> is marked in some way as belonging to all minimal disjunctive normal forms. One says that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696071.png" /> is part of the kernel of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696072.png" /> (is a kernel conjunction). 2) Let the conjunctions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696073.png" /> be marked in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696074.png" /> in the first stage. The remaining conjunctions in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696075.png" /> are ordered, and the inclusion <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696076.png" /> is checked for each such conjunction <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696077.png" />. Conjunctions satisfying this relation do not occur in any minimal disjunctive normal form and are removed from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b01696078.png" />. | ||
| Line 41: | Line 41: | ||
The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960112.png" />-algorithm. The concept employed here is that of a disjunctive normal form that is minimal with respect to a disjunctive normal form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960113.png" />, i.e. one that is minimal among all disjunctive normal forms that are equivalent to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960114.png" /> and are obtained from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960115.png" /> by omission of certain elementary conjunctions. Two properties of an elementary conjunction in a disjunctive normal form are considered: | The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960112.png" />-algorithm. The concept employed here is that of a disjunctive normal form that is minimal with respect to a disjunctive normal form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960113.png" />, i.e. one that is minimal among all disjunctive normal forms that are equivalent to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960114.png" /> and are obtained from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960115.png" /> by omission of certain elementary conjunctions. Two properties of an elementary conjunction in a disjunctive normal form are considered: | ||
| − | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960116.png" /> — | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960116.png" /> — "A occurs in all disjunctive normal forms that are minimal with respect to N" ; and |
| − | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960117.png" /> — | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960117.png" /> — "A occurs in no disjunctive normal form that is minimal with respect to N" . |
It is assumed that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960118.png" /> if the property <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960119.png" /> holds, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960120.png" /> otherwise. It is also assumed that disjunctive normal forms are formed from conjunctions with informative marks <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960121.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960122.png" />. The equality <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960123.png" /> means that the property <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960124.png" /> has not been calculated <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960125.png" />, while the equalities <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960126.png" /> mean that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960127.png" /> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960128.png" />. A conjunction <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960129.png" /> with informative marks (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960130.png" />) is denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960131.png" />. The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960132.png" />-algorithm computes the values of the properties <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960133.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960134.png" /> for the conjunctions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960135.png" /> in the disjunctive normal form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960136.png" />, using for this purpose only the conjunctions of the neighbourhood <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960137.png" /> and their informative marks. For a conjunction <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960138.png" /> of rank <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960139.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960140.png" /> a set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960141.png" /> is called a set of the first type relative to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960142.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960143.png" /> contains conjunctions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960144.png" /> of ranks <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960145.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960146.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960147.png" />. | It is assumed that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960118.png" /> if the property <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960119.png" /> holds, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960120.png" /> otherwise. It is also assumed that disjunctive normal forms are formed from conjunctions with informative marks <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960121.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960122.png" />. The equality <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960123.png" /> means that the property <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960124.png" /> has not been calculated <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960125.png" />, while the equalities <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960126.png" /> mean that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960127.png" /> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960128.png" />. A conjunction <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960129.png" /> with informative marks (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960130.png" />) is denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960131.png" />. The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960132.png" />-algorithm computes the values of the properties <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960133.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960134.png" /> for the conjunctions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960135.png" /> in the disjunctive normal form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960136.png" />, using for this purpose only the conjunctions of the neighbourhood <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960137.png" /> and their informative marks. For a conjunction <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960138.png" /> of rank <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960139.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960140.png" /> a set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960141.png" /> is called a set of the first type relative to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960142.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960143.png" /> contains conjunctions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960144.png" /> of ranks <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960145.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960146.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960147.png" />. | ||
| Line 74: | Line 74: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> S.V. Yablonskii, "Functional constructions in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016960/b016960253.png" />-placed logic" ''Trudy Mat. Inst. Steklov.'' , '''51''' (1958) pp. 5–142 (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> Yu.I. Zhuravlev, "Set-theoretical methods in the algebra of logic" ''Problemy Kibernet.'' , '''8''' (1962) pp. 5–44 (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> W.V. Quine, "On cores and prime implicants of truth functions" ''Amer. Math. Monthly'' , '''66''' (1959) pp. 755–760 {{MR|0108439}} {{ZBL|0201.32203}} </TD></TR></table> |
Revision as of 16:55, 15 April 2012
A representation of Boolean functions by normal forms (cf. Boolean functions, normal forms of) that are most simple relative to some measure of complexity. The usual meaning of the complexity of a normal form is the number of letters in it. A simplest form is then called a minimal form. A measure of complexity sometimes used is the number of elementary conjunctions in a disjunctive normal form or the number of factors in a conjunctive normal form. In this case a simplest form is called a shortest form. In view of the duality of disjunctive and conjunctive normal forms, it is sufficient to consider disjunctive normal forms only.
The construction of shortest and minimal disjunctive normal forms each has its own specific features. The sets of minimal and shortest disjunctive normal forms of one and the same function may be connected by set-theoretical relations: of being contained one in one another, of having an empty intersection or a non-empty symmetric difference. Let 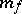 be the complexity of the minimal disjunctive normal form of a function
be the complexity of the minimal disjunctive normal form of a function 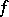 , let
, let 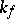 be the minimal complexity of its shortest disjunctive normal form and let
be the minimal complexity of its shortest disjunctive normal form and let 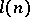 be the largest of the ratios
be the largest of the ratios 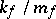 over all functions in
over all functions in  variables. Then the following asymptotic relation holds:
variables. Then the following asymptotic relation holds:
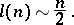 |
By the problem of minimization of Boolean functions one usually understands that of constructing their minimal disjunctive normal forms. There is a trivial algorithm for constructing all minimal disjunctive normal forms of an arbitrary Boolean function 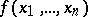 , which operates as follows: All disjunctive normal forms in the variables
, which operates as follows: All disjunctive normal forms in the variables  are reviewed, and those which realize the function
are reviewed, and those which realize the function 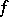 and have minimal complexity are selected. In fact, this algorithm is not applicable even for small
and have minimal complexity are selected. In fact, this algorithm is not applicable even for small  , since the number of operations required increases rapidly. Many other algorithms have therefore been constructed, which, however, are not effectively applicable to all functions.
, since the number of operations required increases rapidly. Many other algorithms have therefore been constructed, which, however, are not effectively applicable to all functions.
The initial specification of a function in the problem of minimization is usually a table, a perfect disjunctive normal form (cf. Boolean functions, normal forms of) or an arbitrary disjunctive normal form. The first stage consists in the transition to the so-called abridged disjunctive normal form, which is uniquely determined for each function. Many methods for the realization of this transition are available. The most universal method consists in performing transformations on a disjunctive normal form of the type
 |
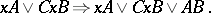 |
A typical property of the abridged disjunctive normal form is that it is possible to obtain any minimal abridged disjunctive normal form from it by removing certain elementary conjunctions. The second, most laborious stage is to extract from the abridged disjunctive normal form all dead-end disjunctive normal forms, among them all the minimal ones. A geometrical representation of Boolean functions is usually employed at this stage. Let 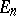 denote the set of all vertices of the
denote the set of all vertices of the  -dimensional unit cube. Each Boolean function
-dimensional unit cube. Each Boolean function 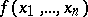 is in one-to-one correspondence with the subset
is in one-to-one correspondence with the subset 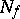 ,
, 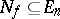 , of vertices
, of vertices 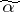 such that
such that 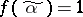 . Let
. Let 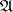 be an elementary conjunction of rank
be an elementary conjunction of rank  . The set
. The set 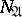 is then called an interval of rank
is then called an interval of rank  corresponding to the elementary conjunction
corresponding to the elementary conjunction 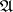 . One says that a system of intervals
. One says that a system of intervals 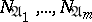 forms a covering of a set
forms a covering of a set 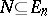 if
if
 |
Since the equalities
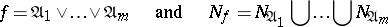 |
are equivalent, the problem of minimization of Boolean functions is equivalent to the search for coverings with a minimal sum of the ranks of their intervals. Such coverings are called minimal. An interval 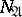 is called maximal for a function
is called maximal for a function 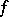 if
if  and if there is no interval
and if there is no interval  such that
such that 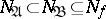 . The construction of dead-end disjunctive normal forms of a function
. The construction of dead-end disjunctive normal forms of a function 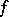 reduces to a search for coverings of
reduces to a search for coverings of 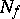 by maximal intervals such that no proper subset of it is a covering of
by maximal intervals such that no proper subset of it is a covering of 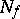 . These coverings correspond to dead-end disjunctive normal forms and are called irreducible. They are obtained from coverings corresponding to abridged disjunctive normal forms by removal of certain intervals.
. These coverings correspond to dead-end disjunctive normal forms and are called irreducible. They are obtained from coverings corresponding to abridged disjunctive normal forms by removal of certain intervals.
The selection of the minimal disjunctive normal forms from all dead-end disjunctive normal forms is also a very laborious process, since "almost-all" Boolean functions in  arguments have no fewer than
arguments have no fewer than 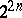 different dead-end disjunctive normal forms. The diversity of the complexities of dead-end disjunctive normal forms may be very wide, so that if a random rather than a dead-end minimal disjunctive normal form is selected, a large error may result.
different dead-end disjunctive normal forms. The diversity of the complexities of dead-end disjunctive normal forms may be very wide, so that if a random rather than a dead-end minimal disjunctive normal form is selected, a large error may result.
Estimates of the number of dead-end disjunctive normal forms and of the scatter of their complexities show that a more detailed inspection during the elimination of the elementary conjunctions from a disjunctive normal form is a natural way of improving the effectiveness of minimization algorithms. A conjunction should be eliminated (or, on the contrary, retained until the end of the process) only if it can be established by some procedure that it does not occur in any minimal disjunctive normal form for  (occurs in all minimal disjunctive normal forms for
(occurs in all minimal disjunctive normal forms for 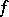 ). The latter fact is usually established by an analysis of the conjunctions that are close to the one in question, i.e. occur in a neighbourhood of it (cf. Algorithm, local). Here one has to accumulate information about elementary conjunctions and use it in the subsequent analysis. Procedures of this kind are known as local simplification algorithms. Some of them are quoted below, and their description involves the concept of the
). The latter fact is usually established by an analysis of the conjunctions that are close to the one in question, i.e. occur in a neighbourhood of it (cf. Algorithm, local). Here one has to accumulate information about elementary conjunctions and use it in the subsequent analysis. Procedures of this kind are known as local simplification algorithms. Some of them are quoted below, and their description involves the concept of the 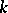 -th order neighbourhood
-th order neighbourhood 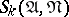 of an elementary conjunction
of an elementary conjunction 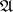 in a disjunctive normal form
in a disjunctive normal form  ,
, 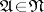 .
.
The zero-order neighbourhood  consists of the single conjunction
consists of the single conjunction 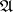 . If
. If 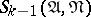 is the neighbourhood of order
is the neighbourhood of order 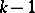 , then the neighbourhood
, then the neighbourhood  of order
of order 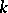 consists of all conjunctions
consists of all conjunctions 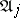 of the disjunctive normal form
of the disjunctive normal form 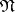 that satisfy one of the following conditions: 1)
that satisfy one of the following conditions: 1) 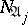 has a non-empty intersection with at least one interval corresponding to a conjunction of
has a non-empty intersection with at least one interval corresponding to a conjunction of 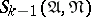 ; or 2)
; or 2) 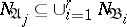 , where
, where  ,
, 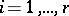 , satisfies 1).
, satisfies 1).
Quine's algorithm. Here one considers at each step the neighbourhood 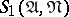 of one of the conjunctions in the disjunctive normal form
of one of the conjunctions in the disjunctive normal form 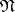 . As the algorithm is executed for each conjunction, one attempts to compute one of the following properties:
. As the algorithm is executed for each conjunction, one attempts to compute one of the following properties:
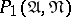 — "A occurs in all minimal disjunctive normal forms" ; and
— "A occurs in all minimal disjunctive normal forms" ; and
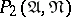 — "A does not occur in any minimal disjunctive normal form" .
— "A does not occur in any minimal disjunctive normal form" .
The algorithm works as follows. 1) The neighbourhood 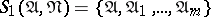 is successively formed for each conjunction
is successively formed for each conjunction  in
in 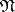 . The inclusion
. The inclusion 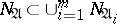 is verified. If this is not the case, then
is verified. If this is not the case, then 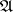 is marked in some way as belonging to all minimal disjunctive normal forms. One says that
is marked in some way as belonging to all minimal disjunctive normal forms. One says that 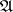 is part of the kernel of
is part of the kernel of 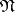 (is a kernel conjunction). 2) Let the conjunctions
(is a kernel conjunction). 2) Let the conjunctions 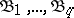 be marked in
be marked in 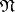 in the first stage. The remaining conjunctions in
in the first stage. The remaining conjunctions in 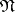 are ordered, and the inclusion
are ordered, and the inclusion 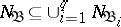 is checked for each such conjunction
is checked for each such conjunction  . Conjunctions satisfying this relation do not occur in any minimal disjunctive normal form and are removed from
. Conjunctions satisfying this relation do not occur in any minimal disjunctive normal form and are removed from 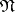 .
.
Regular points algorithm. During each step of this algorithm one examines the neighbourhood 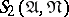 of a conjunction
of a conjunction 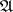 in the disjunctive normal form
in the disjunctive normal form 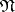 , and the conjunctions not occurring in any dead-end disjunctive normal form, and hence not occurring in any minimal disjunctive normal form either, are eliminated. The description of the algorithm involves the concept of an
, and the conjunctions not occurring in any dead-end disjunctive normal form, and hence not occurring in any minimal disjunctive normal form either, are eliminated. The description of the algorithm involves the concept of an  -bundle in
-bundle in 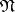 , which, for this point
, which, for this point 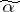 in
in 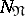 , is the set
, is the set 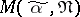 of intervals
of intervals 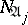 such that
such that 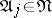 ,
, 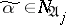 . For a conjunction
. For a conjunction 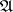 in
in 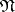 a point
a point  of
of 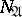 is called regular with respect to
is called regular with respect to 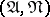 if there exists a point
if there exists a point 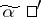 such that
such that 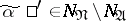 and
and 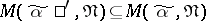 . A set
. A set 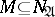 is called regular with respect to
is called regular with respect to 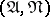 if all its points are regular with respect to
if all its points are regular with respect to 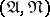 . This algorithm is based on the fact that a conjunction
. This algorithm is based on the fact that a conjunction 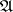 of the abridged disjunctive normal form of a function
of the abridged disjunctive normal form of a function 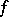 does not occur in any dead-end disjunctive normal form of
does not occur in any dead-end disjunctive normal form of 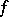 if and only if
if and only if 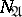 is a regular set with respect to
is a regular set with respect to 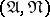 . The algorithm checks whether in a certain sequence the conjunction intervals occurring in the disjunctive normal form are regular sets and eliminates those that are regular. Whether or not an interval
. The algorithm checks whether in a certain sequence the conjunction intervals occurring in the disjunctive normal form are regular sets and eliminates those that are regular. Whether or not an interval 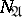 is regular with respect to
is regular with respect to 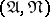 is completely determined by the neighbourhood
is completely determined by the neighbourhood 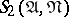 but not, in general, by the neighbourhood
but not, in general, by the neighbourhood 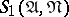 .
.
The 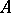 -algorithm. The concept employed here is that of a disjunctive normal form that is minimal with respect to a disjunctive normal form
-algorithm. The concept employed here is that of a disjunctive normal form that is minimal with respect to a disjunctive normal form 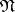 , i.e. one that is minimal among all disjunctive normal forms that are equivalent to
, i.e. one that is minimal among all disjunctive normal forms that are equivalent to 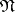 and are obtained from
and are obtained from 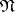 by omission of certain elementary conjunctions. Two properties of an elementary conjunction in a disjunctive normal form are considered:
by omission of certain elementary conjunctions. Two properties of an elementary conjunction in a disjunctive normal form are considered:
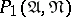 — "A occurs in all disjunctive normal forms that are minimal with respect to N" ; and
— "A occurs in all disjunctive normal forms that are minimal with respect to N" ; and
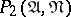 — "A occurs in no disjunctive normal form that is minimal with respect to N" .
— "A occurs in no disjunctive normal form that is minimal with respect to N" .
It is assumed that 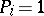 if the property
if the property 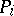 holds, and
holds, and 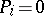 otherwise. It is also assumed that disjunctive normal forms are formed from conjunctions with informative marks
otherwise. It is also assumed that disjunctive normal forms are formed from conjunctions with informative marks 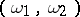 , where
, where 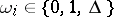 . The equality
. The equality 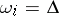 means that the property
means that the property 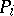 has not been calculated
has not been calculated 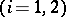 , while the equalities
, while the equalities 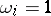 mean that
mean that 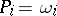
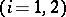 . A conjunction
. A conjunction 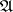 with informative marks (
with informative marks (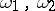 ) is denoted by
) is denoted by 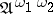 . The
. The  -algorithm computes the values of the properties
-algorithm computes the values of the properties  and
and 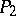 for the conjunctions
for the conjunctions 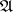 in the disjunctive normal form
in the disjunctive normal form 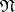 , using for this purpose only the conjunctions of the neighbourhood
, using for this purpose only the conjunctions of the neighbourhood 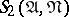 and their informative marks. For a conjunction
and their informative marks. For a conjunction  of rank
of rank  of
of 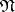 a set
a set 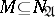 is called a set of the first type relative to
is called a set of the first type relative to 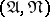 if
if 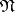 contains conjunctions
contains conjunctions 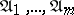 of ranks
of ranks 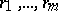 such that
such that 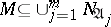 and
and 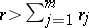 .
.
The difference 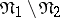 of two disjunctive normal forms
of two disjunctive normal forms 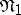 and
and 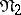 is the disjunctive normal form consisting of the elementary conjunctions occurring in
is the disjunctive normal form consisting of the elementary conjunctions occurring in 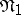 but not in
but not in 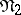 .
.
Before the application of the 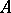 -algorithm all conjunctions of the disjunctive normal form
-algorithm all conjunctions of the disjunctive normal form 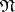 have the mark
have the mark 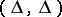 . After
. After 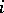 steps have been performed and the conjunctions
steps have been performed and the conjunctions 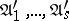 have received the mark
have received the mark 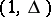 , and the conjunctions
, and the conjunctions  have received the mark
have received the mark 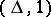 , the
, the 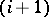 -th step consists of the following. The conjunctions in the disjunctive normal form are ordered in some way. If the disjunctive normal form
-th step consists of the following. The conjunctions in the disjunctive normal form are ordered in some way. If the disjunctive normal form 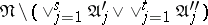 is empty, the
is empty, the  -algorithm is terminated. If it is not, the conjunctions of this disjunctive normal form are ordered in some way; the first conjunction
-algorithm is terminated. If it is not, the conjunctions of this disjunctive normal form are ordered in some way; the first conjunction  in the sequence and its neighbourhoods
in the sequence and its neighbourhoods 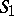 and
and 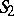 in the disjunctive normal form
in the disjunctive normal form 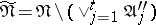 are singled out, and the relation
are singled out, and the relation
 |
is checked. If it is satisfied, the mark 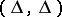 over
over 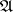 is replaced by
is replaced by 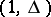 and the
and the 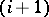 -th step of the
-th step of the 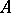 -algorithm is terminated. If not, then a check is made whether or not
-algorithm is terminated. If not, then a check is made whether or not 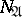 can be represented in the form
can be represented in the form 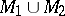 , where
, where 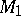 is a regular set relative to
is a regular set relative to 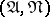 and
and 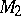 is a set of the first type relative to
is a set of the first type relative to 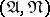 . If
. If  can be represented in this form, the mark
can be represented in this form, the mark 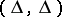 over
over 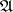 is replaced by
is replaced by 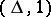 and the
and the 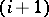 -th step of the
-th step of the 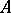 -algorithm is terminated; if this is not possible, the procedure is applied to the second conjunction in the sequence, etc. If the mark does not change in any one of these conjunctions, then after all the conjunctions have been examined, the operation of the
-algorithm is terminated; if this is not possible, the procedure is applied to the second conjunction in the sequence, etc. If the mark does not change in any one of these conjunctions, then after all the conjunctions have been examined, the operation of the  -algorithm is terminated.
-algorithm is terminated.
If the abridged disjunctive normal form 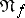 of a function
of a function 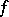 is taken for
is taken for 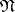 , then no conjunctions that obtained in the algorithm the mark
, then no conjunctions that obtained in the algorithm the mark 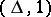 occur in any minimal disjunctive normal form of
occur in any minimal disjunctive normal form of 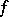 ; they are eliminated from
; they are eliminated from 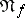 . Conjunctions that obtained the mark
. Conjunctions that obtained the mark 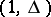 occur in all minimal disjunctive normal forms of
occur in all minimal disjunctive normal forms of 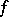 . Various special cases of the
. Various special cases of the 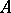 -algorithm have also been considered.
-algorithm have also been considered.
The ring algorithm places over the conjunctions informative marks 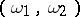 , with the same meaning as in the
, with the same meaning as in the  -algorithm. At each step of the ring algorithm use is made of the conjunctions contained in the
-algorithm. At each step of the ring algorithm use is made of the conjunctions contained in the 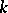 -th order neighbourhood of some conjunction and of their informative marks. A simplified version of this algorithm is outlined below. The ring algorithm in its complete form is the best local algorithm with a special memory relative to the neighbourhoods
-th order neighbourhood of some conjunction and of their informative marks. A simplified version of this algorithm is outlined below. The ring algorithm in its complete form is the best local algorithm with a special memory relative to the neighbourhoods 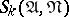 . The algorithms described above are special cases of the general ring algorithm. If
. The algorithms described above are special cases of the general ring algorithm. If
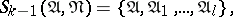 |
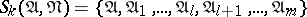 |
and
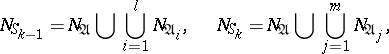 |
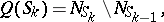 |
then to each subset 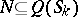 a Boolean function
a Boolean function 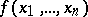 that is not everywhere defined is assigned, such that the set
that is not everywhere defined is assigned, such that the set  of its ones is
of its ones is 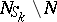 and the set
and the set 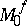 of its zeros is
of its zeros is 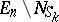 ; the function
; the function 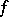 is not defined on
is not defined on 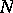 . The set of such functions is denoted by
. The set of such functions is denoted by 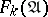 . Prior to the beginning of the algorithm the conjunctions of the disjunctive normal form
. Prior to the beginning of the algorithm the conjunctions of the disjunctive normal form 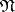 in question have the mark
in question have the mark 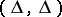 . If, after
. If, after 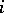 steps have been completed, conjunctions
steps have been completed, conjunctions 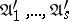 with the mark
with the mark  and conjunctions
and conjunctions  with the mark
with the mark 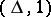 are obtained, then the
are obtained, then the 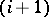 -th step is performed as follows. The conjunctions of the disjunctive normal forms are ordered in some way. If the disjunctive normal form
-th step is performed as follows. The conjunctions of the disjunctive normal forms are ordered in some way. If the disjunctive normal form 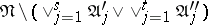 is empty, the algorithm is terminated. If not, then all conjunctions of this disjunctive normal form are ordered in some way. For the conjunction
is empty, the algorithm is terminated. If not, then all conjunctions of this disjunctive normal form are ordered in some way. For the conjunction 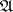 which is the first in the sequence and for all
which is the first in the sequence and for all 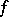 from the set
from the set  , all disjunctive normal forms which realize
, all disjunctive normal forms which realize 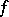 on its domain of definition, which consist of conjunctions in
on its domain of definition, which consist of conjunctions in 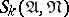 and which contain the least number of variable symbols as compared with other such disjunctive normal forms, are found. Among them one selects all disjunctive normal forms which, first, do not contain the conjunctions
and which contain the least number of variable symbols as compared with other such disjunctive normal forms, are found. Among them one selects all disjunctive normal forms which, first, do not contain the conjunctions  and, secondly, contain all the conjunctions
and, secondly, contain all the conjunctions 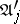 ,
, 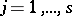 , for which
, for which 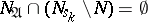 . If for all
. If for all 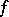 in
in  the conjunction
the conjunction 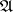 occurs in all disjunctive normal forms selected, then the mark
occurs in all disjunctive normal forms selected, then the mark 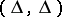 over
over 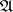 is replaced by
is replaced by 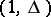 and the
and the 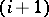 -th step of the algorithm is terminated. If
-th step of the algorithm is terminated. If 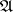 does not occur in any disjunctive normal form selected, then the mark
does not occur in any disjunctive normal form selected, then the mark 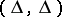 is changed into
is changed into 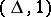 and the
and the 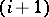 -th step of the algorithm is terminated. Otherwise, the procedure just described is applied to the conjunction that is next in sequence, etc. If the mark cannot be changed for any conjunction, the algorithm terminates at the
-th step of the algorithm is terminated. Otherwise, the procedure just described is applied to the conjunction that is next in sequence, etc. If the mark cannot be changed for any conjunction, the algorithm terminates at the 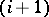 -th step. All conjunctions obtained in the ring algorithm over the abridged disjunctive normal form
-th step. All conjunctions obtained in the ring algorithm over the abridged disjunctive normal form 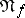 of a function
of a function 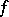 with mark
with mark 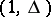 (or, respectively,
(or, respectively, 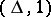 ) occur in all minimal disjunctive normal forms (or, do not occur in any minimal disjunctive normal form) of
) occur in all minimal disjunctive normal forms (or, do not occur in any minimal disjunctive normal form) of 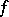 . The algorithms just described yield identical results, whatever the manner of ordering of the conjunctions in the disjunctive normal form.
. The algorithms just described yield identical results, whatever the manner of ordering of the conjunctions in the disjunctive normal form.
The task of selecting all conjunctions occurring in at least one or not occurring in any minimal disjunctive normal form cannot be solved by algorithms working with 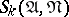 if
if 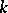 is bounded or increases too slowly as the number of variables
is bounded or increases too slowly as the number of variables  increases. This situation does not change if to the properties
increases. This situation does not change if to the properties 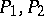 stored in the algorithm a bounded set of properties or one that increases too slowly as
stored in the algorithm a bounded set of properties or one that increases too slowly as  increases is added.
increases is added.
References
| [1] | S.V. Yablonskii, "Functional constructions in 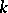 -placed logic" Trudy Mat. Inst. Steklov. , 51 (1958) pp. 5–142 (In Russian) -placed logic" Trudy Mat. Inst. Steklov. , 51 (1958) pp. 5–142 (In Russian) |
| [2] | Yu.I. Zhuravlev, "Set-theoretical methods in the algebra of logic" Problemy Kibernet. , 8 (1962) pp. 5–44 (In Russian) |
| [3] | W.V. Quine, "On cores and prime implicants of truth functions" Amer. Math. Monthly , 66 (1959) pp. 755–760 MR0108439 Zbl 0201.32203 |
Boolean functions, minimization of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Boolean_functions,_minimization_of&oldid=17510