Difference between revisions of "Unimodular element"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 6: | Line 6: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A.J. Hahn, O.T. O'Meara, "The classical groups and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095340/u09534022.png" />-theory" , Springer (1989) pp. 9, §141ff {{MR|1007302}} {{ZBL|}} </TD></TR></table> |
Revision as of 17:35, 31 March 2012
unimodular vector
Let 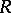 be a ring with unit and
be a ring with unit and 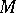 a right module over
a right module over 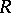 . An element
. An element  in
in 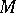 is called unimodular if
is called unimodular if  and the submodule
and the submodule 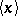 generated by
generated by  has a complement
has a complement 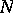 in
in  , i.e. there is a submodule
, i.e. there is a submodule 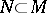 such that
such that  ,
,  , so that
, so that 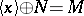 .
.
An element of a free module 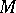 that is part of a basis of
that is part of a basis of 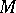 is unimodular. An element
is unimodular. An element 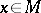 is unimodular if and only if there is a homomorphism of modules
is unimodular if and only if there is a homomorphism of modules 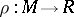 such that
such that 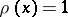 . A row (or column) of a unimodular matrix over
. A row (or column) of a unimodular matrix over 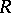 is unimodular. The question when the converse is true is important in algebraic
is unimodular. The question when the converse is true is important in algebraic  -theory. Cf. also Stable rank.
-theory. Cf. also Stable rank.
References
| [a1] | A.J. Hahn, O.T. O'Meara, "The classical groups and 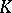 -theory" , Springer (1989) pp. 9, §141ff MR1007302 -theory" , Springer (1989) pp. 9, §141ff MR1007302 |
How to Cite This Entry:
Unimodular element. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Unimodular_element&oldid=17441
Unimodular element. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Unimodular_element&oldid=17441