Difference between revisions of "Fubini theorem"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 12: | Line 12: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> G. Fubini, "Sugli integrali multipli" , ''Opere scelte'' , '''2''' , Cremonese (1958) pp. 243–249</TD></TR></table> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> G. Fubini, "Sugli integrali multipli" , ''Opere scelte'' , '''2''' , Cremonese (1958) pp. 243–249 {{MR|}} {{ZBL|38.0343.02}} </TD></TR></table> |
Revision as of 11:59, 27 September 2012
A theorem that establishes a connection between a multiple integral and a repeated one. Suppose that 
and 
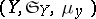are measure spaces with 
-finite complete measures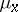 
and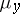 
defined on the 
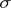-algebras 
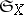and 
, respectively. If the function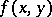 
is integrable on the product 
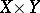of 
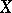and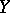 
with respect to the product measure 
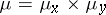of 
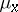and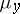 
, then for almost-all 
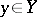the function 
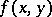of the variable 
is integrable on 
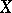with respect to 
, the function 
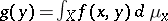is integrable on 
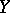with respect to 
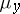, and one has the equality
 | (1) |
Fubini's theorem is valid, in particular, for the case when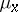 
, 
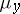and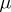 
are the Lebesgue measures in the Euclidean spaces 
, 
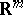and 
respectively (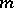
and 
are natural numbers), 
, 
, 
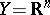, and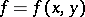 
is a Lebesgue-measurable function on 
, 
, 
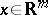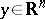. Under these assumptions, formula (1) has the form
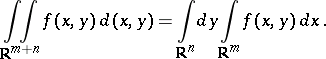 | (2) |
In the case of a function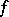 
defined on an arbitrary Lebesgue-measurable set 
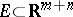, in order to express the multiple integral in terms of a repeated one, one must extend 
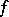by zero to the whole of 
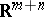and apply (2). See also Repeated integral.
The theorem was established by G. Fubini [1].
References
| [1] | G. Fubini, "Sugli integrali multipli" , Opere scelte , 2 , Cremonese (1958) pp. 243–249 Zbl 38.0343.02 |
Fubini theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fubini_theorem&oldid=17242