Difference between revisions of "Partially balanced incomplete block design"
(Importing text file) |
|||
| Line 1: | Line 1: | ||
''PBIBD'' | ''PBIBD'' | ||
| − | A (symmetric) association scheme with | + | A (symmetric) association scheme with $m$ classes on the $v$ symbols $\{1,...,v\}$ satisfies: |
| − | Two distinct symbols | + | Two distinct symbols $x$ and $y$ are termed $i$th associates for exactly one $i\in\{1,...,m\}$; each symbol has exactly $n_i$ $i$th associates; and when two distinct symbols $x$ and $y$ are $i$th associates, the number of other symbols that are $j$th associates of $x$ and also $k$th associates of $y$ is $p^i_jk$, independent of the choice of the $i$th associates $x$ and $y$. The matrices $A_0,...,A_m$ of an $m$-class association scheme are defined as $A_0=I$, and for $1\leq \leq m$, $A_i$ is a $(0,1)$-matrix whose entry $(x,y)$ is $1$ exactly when $x$ and $y$ are $i$th associates. |
| − | each symbol | + | Let $X$ be a $v$-set with a symmetric $m$-class association scheme defined on it. A partially balanced incomplete block design with $m$ associate classes (or $\mathrm{PBIBD}(m)$) is a [[Block design|block design]] based on $X$ with $b$ sets (the blocks), each of size $k$, and with each symbol appearing in $r$ blocks. Any two symbols that are $i$th associates appear together in $\lambda_i$ blocks of $\mathrm{PBIBD}(m)$. The numbers $v,b,r,k,\lambda_i$ ($1\leq i\leq m$) are the parameters of $\mathrm{PBIBD}(m)$. The notation $\mathrm{PBIBD}(v,k,\lambda_i)$ is also used. $N$ is used for the $v\times b$ $(0,1)$ incidence matrix of $\mathrm{PBIBD}(m)$. |
| − | + | Let $A_0,...,A_m$ be the matrices of an association scheme corresponding to a $\mathrm{PBIBD}(m)$. Then $NN^T=rI+\sum_i\lambda_iA_i$ and $JN=kJ$. Conversely, if $N$ is a $(0,1)$-matrix which satisfies these conditions and the $A_i$ are the matrices of an association scheme, then $N$ is the incidence matrix of a $\mathrm{PBIBD}(m)$. | |
| − | |||
| − | Let | ||
| − | |||
| − | |||
It is easily verified that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120080/p12008061.png" />, that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120080/p12008062.png" />, and that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120080/p12008063.png" />. A <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120080/p12008064.png" /> is a balanced incomplete block design (a BIBD; cf. [[Block design|Block design]]); also, a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120080/p12008065.png" /> in which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120080/p12008066.png" /> is a BIBD. | It is easily verified that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120080/p12008061.png" />, that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120080/p12008062.png" />, and that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120080/p12008063.png" />. A <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120080/p12008064.png" /> is a balanced incomplete block design (a BIBD; cf. [[Block design|Block design]]); also, a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120080/p12008065.png" /> in which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120080/p12008066.png" /> is a BIBD. | ||
Revision as of 03:02, 23 December 2020
PBIBD
A (symmetric) association scheme with $m$ classes on the $v$ symbols $\{1,...,v\}$ satisfies:
Two distinct symbols $x$ and $y$ are termed $i$th associates for exactly one $i\in\{1,...,m\}$; each symbol has exactly $n_i$ $i$th associates; and when two distinct symbols $x$ and $y$ are $i$th associates, the number of other symbols that are $j$th associates of $x$ and also $k$th associates of $y$ is $p^i_jk$, independent of the choice of the $i$th associates $x$ and $y$. The matrices $A_0,...,A_m$ of an $m$-class association scheme are defined as $A_0=I$, and for $1\leq \leq m$, $A_i$ is a $(0,1)$-matrix whose entry $(x,y)$ is $1$ exactly when $x$ and $y$ are $i$th associates.
Let $X$ be a $v$-set with a symmetric $m$-class association scheme defined on it. A partially balanced incomplete block design with $m$ associate classes (or $\mathrm{PBIBD}(m)$) is a block design based on $X$ with $b$ sets (the blocks), each of size $k$, and with each symbol appearing in $r$ blocks. Any two symbols that are $i$th associates appear together in $\lambda_i$ blocks of $\mathrm{PBIBD}(m)$. The numbers $v,b,r,k,\lambda_i$ ($1\leq i\leq m$) are the parameters of $\mathrm{PBIBD}(m)$. The notation $\mathrm{PBIBD}(v,k,\lambda_i)$ is also used. $N$ is used for the $v\times b$ $(0,1)$ incidence matrix of $\mathrm{PBIBD}(m)$.
Let $A_0,...,A_m$ be the matrices of an association scheme corresponding to a $\mathrm{PBIBD}(m)$. Then $NN^T=rI+\sum_i\lambda_iA_i$ and $JN=kJ$. Conversely, if $N$ is a $(0,1)$-matrix which satisfies these conditions and the $A_i$ are the matrices of an association scheme, then $N$ is the incidence matrix of a $\mathrm{PBIBD}(m)$.
It is easily verified that 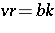 , that
, that 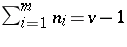 , and that
, and that 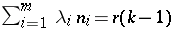 . A
. A  is a balanced incomplete block design (a BIBD; cf. Block design); also, a
is a balanced incomplete block design (a BIBD; cf. Block design); also, a 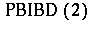 in which
in which  is a BIBD.
is a BIBD.
There are six types of 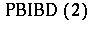 s, [a3], based on the underlying types of association schemes:
s, [a3], based on the underlying types of association schemes:
1) group divisible;
2) triangular;
3) Latin-square-type;
4) cyclic;
5) partial-geometry-type; and
6) miscellaneous.
Partition the 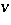 -set
-set 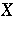 into
into 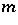 groups each of size
groups each of size 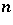 . In a group-divisible association scheme the first associates are the symbols in the same group and the second associates are all the other symbols. The eigenvalues of
. In a group-divisible association scheme the first associates are the symbols in the same group and the second associates are all the other symbols. The eigenvalues of  are
are  ,
,  and
and  , with multiplicities
, with multiplicities 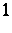 ,
, 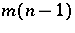 , and
, and  , respectively. A group-divisible partially balanced incomplete block design is singular if
, respectively. A group-divisible partially balanced incomplete block design is singular if  ; semi-regular if
; semi-regular if 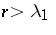 ,
, 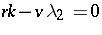 ; and regular if
; and regular if 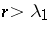 and
and 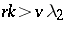 .
.
Let 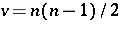 ,
,  , and arrange the
, and arrange the  elements of
elements of 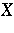 in a symmetrical
in a symmetrical 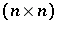 -array with the diagonal entries blank. In the triangular association scheme, the first associates of a symbol are those in the same row or column of the array; all other symbols are second associates. The duals of triangular
-array with the diagonal entries blank. In the triangular association scheme, the first associates of a symbol are those in the same row or column of the array; all other symbols are second associates. The duals of triangular 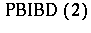 s are the residual designs of symmetric BIBDs with
s are the residual designs of symmetric BIBDs with 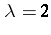 . Triangular schemes and generalized triangular schemes are also known as Johnson schemes.
. Triangular schemes and generalized triangular schemes are also known as Johnson schemes.
Let 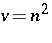 and arrange the
and arrange the 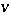 symbols in an
symbols in an 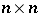 array. Superimpose on this array a set of
array. Superimpose on this array a set of 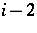 mutually orthogonal Latin squares (see [a1] and also Latin square) of order
mutually orthogonal Latin squares (see [a1] and also Latin square) of order 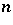 . Let the first associates of any symbol be those in the same row or column of the array or be associated with the same symbols in one of the Latin squares. This is an
. Let the first associates of any symbol be those in the same row or column of the array or be associated with the same symbols in one of the Latin squares. This is an  -type association scheme. If
-type association scheme. If 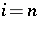 , then the scheme is group divisible; if
, then the scheme is group divisible; if 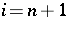 , then all the symbols are first associates of each other.
, then all the symbols are first associates of each other.
Let 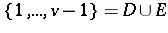 . A non-group divisible association scheme defined on
. A non-group divisible association scheme defined on 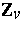 is cyclic if
is cyclic if 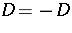 and if the set of
and if the set of 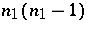 differences of distinct elements of
differences of distinct elements of 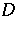 has each element of
has each element of 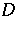
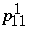 times and each element of
times and each element of 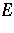
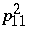 times. The first associates of
times. The first associates of 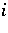 are
are 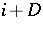 .
.
In a partial-geometry-type association scheme, two symbols are first associates if they are incident with a line of the geometry and second associates if they are not incident with a line of the geometry.
See [a2], [a4], [a5] for further information.
References
| [a1] | R.J.R. Abel, A.E. Brouwer, C.J. Colbourn, J.H. Dinitz, "Mutually orthogonal latin squares" C.J. Colbourn (ed.) J.H. Dinitz (ed.) , CRC Handbook of Combinatorial Designs , CRC (1996) pp. 111–141 |
| [a2] | R.A. Bailey, "Partially balanced designs" N.L. Johnson (ed.) S. Kotz (ed.) C. Read (ed.) , Encycl. Stat. Sci. , 6 , Wiley (1985) pp. 593–610 |
| [a3] | W.H. Clatworthy, "Tables of two-associate-class partially balanced designs" , Applied Math. Ser. , 63 , Nat. Bureau of Standards (US) (1973) |
| [a4] | D. Raghavarao, "Constructions and combinatorial problems in design of experiments" , Wiley (1971) |
| [a5] | D.J. Street, A.P. Street, "Partially balanced incomplete block designs" C.J. Colbourn (ed.) J.H. Dinitz (ed.) , CRC Handbook of Combinatorial Designs , CRC (1996) pp. 419–423 |
Partially balanced incomplete block design. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Partially_balanced_incomplete_block_design&oldid=17069