Difference between revisions of "Co-algebra"
(Importing text file) |
(TeX partly done) |
||
| Line 1: | Line 1: | ||
| − | A module | + | A module $A$ over a commutative ring $k$ with two homomorphisms $\phi$ and $\epsilon$ such that the diagrams |
| − | + | $$ | |
| − | + | \begin{array}{ccc} A & \stackrel{\phi}{\rightarrow} & A \otimes A \\ \phi\,\downarrow & \ & \downarrow\,1 \otimes \phi \\ A \otimes A & \stackrel{\phi \otimes 1}{\longrightarrow} & A \otimes A \end{array} | |
| − | + | $$ | |
and | and | ||
Revision as of 19:01, 10 April 2017
A module $A$ over a commutative ring $k$ with two homomorphisms $\phi$ and $\epsilon$ such that the diagrams $$ \begin{array}{ccc} A & \stackrel{\phi}{\rightarrow} & A \otimes A \\ \phi\,\downarrow & \ & \downarrow\,1 \otimes \phi \\ A \otimes A & \stackrel{\phi \otimes 1}{\longrightarrow} & A \otimes A \end{array} $$ and
 |
are commutative. In other words, a co-algebra is the dual concept (in the sense of category theory) to the concept of an associative algebra over a ring 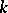 .
.
Co-algebras have acquired significance in connection with a number of topological applications such as, for example, the simplicial complex of a topological space, which is a co-algebra. Closely related to co-algebras are the Hopf algebras, which possess algebra and co-algebra structures simultaneously (cf. Hopf algebra).
References
| [1] | S. MacLane, "Homology" , Springer (1963) |
Comments
Given a co-algebra 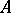 over
over 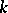 . Let
. Let  be the module of
be the module of 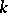 -module homomorphisms from
-module homomorphisms from 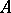 to
to 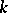 . For
. For 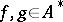 define the product
define the product 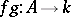 by the formula
by the formula 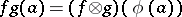 , where
, where 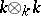 is identified with
is identified with 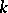 . For any two
. For any two 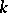 -modules
-modules 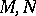 define
define 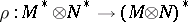 by
by 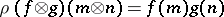 . Then the multiplication on
. Then the multiplication on 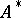 can also be seen as the composite
can also be seen as the composite 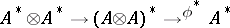 . The element
. The element 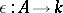 is a unit element for this multiplication making
is a unit element for this multiplication making 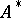 an associative algebra with unit, the dual algebra. In general the mapping
an associative algebra with unit, the dual algebra. In general the mapping 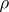 is not an isomorphism and there is no natural
is not an isomorphism and there is no natural 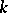 -module homomorphism
-module homomorphism 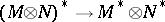 . Thus there is no equally natural construction associating a co-algebra to an algebra over
. Thus there is no equally natural construction associating a co-algebra to an algebra over 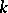 , even when
, even when 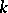 is a field. In that case there does however exist an adjoint functor
is a field. In that case there does however exist an adjoint functor 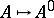 to the functor
to the functor 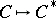 which associates to a co-algebra its dual algebra, i.e.
which associates to a co-algebra its dual algebra, i.e. 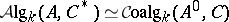 for
for 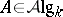 ,
, 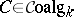 , where
, where 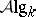 and
and 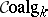 denote, respectively, the category of
denote, respectively, the category of 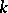 -algebras and the category of
-algebras and the category of 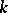 -co-algebras, [a2]; cf. also Hopf algebra. But if
-co-algebras, [a2]; cf. also Hopf algebra. But if 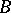 is free of finite rank over
is free of finite rank over 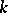 then
then 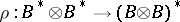 is an isomorphism and the dual co-algebra can be defined.
is an isomorphism and the dual co-algebra can be defined.
Let 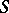 be the set
be the set 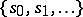 . Let
. Let 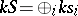 and define
and define
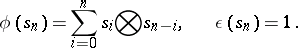 |
Then 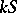 is a co-algebra.
is a co-algebra.
If 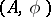 and
and 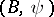 are two co-algebras, then a morphism of co-algebras is a
are two co-algebras, then a morphism of co-algebras is a 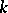 -module morphism
-module morphism 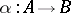 such that
such that 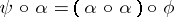 and
and 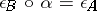 . A co-ideal of a co-algebra
. A co-ideal of a co-algebra 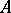 is a
is a 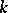 -submodule
-submodule 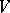 such that
such that 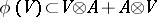 and
and 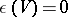 .
.
A co-module 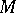 over a co-algebra
over a co-algebra 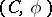 is a
is a 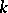 -module with a
-module with a 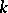 -module morphism
-module morphism 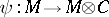 such that
such that 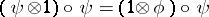 and
and 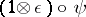 the canonical isomorphism
the canonical isomorphism 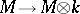 . There are obvious notions of homomorphisms of co-modules, etc.
. There are obvious notions of homomorphisms of co-modules, etc.
References
| [a1] | M. Sweedler, "Hopf algebras" , Benjamin (1969) |
| [a2] | E. Abe, "Hopf algebras" , Cambridge Univ. Press (1980) |
Co-algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Co-algebra&oldid=16415