Difference between revisions of "Maximal torus"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 20: | Line 20: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Borel, "Linear algebraic groups" , Benjamin (1969) {{MR|0251042}} {{ZBL|0206.49801}} {{ZBL|0186.33201}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A. Borel (ed.) G.D. Mostow (ed.) , ''Algebraic groups and discontinuous subgroups'' , ''Proc. Symp. Pure Math.'' , '''9''' , Amer. Math. Soc. (1966) {{MR|0202512}} {{ZBL|0171.24105}} </TD></TR></table> |
====Comments==== | ====Comments==== | ||
| Line 32: | Line 32: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> L.S. Pontryagin, "Topological groups" , Princeton Univ. Press (1958) (Translated from Russian) {{MR|0201557}} {{ZBL|0022.17104}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> D.P. Zhelobenko, "Compact Lie groups and their representations" , Amer. Math. Soc. (1973) (Translated from Russian) {{MR|0473097}} {{MR|0473098}} {{ZBL|0228.22013}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978) {{MR|0514561}} {{ZBL|0451.53038}} </TD></TR></table> |
| Line 40: | Line 40: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> N. Bourbaki, "Groupes et algèbres de Lie" , ''Eléments de mathématiques'' , Masson (1982) pp. Chapt. 9. Groupes de Lie réels compacts {{MR|0682756}} {{ZBL|0505.22006}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> Th. Bröcker, T. Tom Dieck, "Representations of compact Lie groups" , Springer (1985) {{MR|0781344}} {{ZBL|0581.22009}} </TD></TR></table> |
Revision as of 14:50, 24 March 2012
A maximal torus of a linear algebraic group 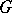 is an algebraic subgroup of
is an algebraic subgroup of  which is an algebraic torus and which is not contained in any larger subgroup of that type. Now let
which is an algebraic torus and which is not contained in any larger subgroup of that type. Now let 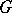 be connected. The union of all maximal tori of
be connected. The union of all maximal tori of 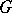 coincides with the set of all semi-simple elements of
coincides with the set of all semi-simple elements of  (see Jordan decomposition) and their intersection coincides with the set of all semi-simple elements of the centre of
(see Jordan decomposition) and their intersection coincides with the set of all semi-simple elements of the centre of 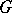 . Every maximal torus is contained in some Borel subgroup of
. Every maximal torus is contained in some Borel subgroup of 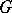 . The centralizer of a maximal torus is a Cartan subgroup of
. The centralizer of a maximal torus is a Cartan subgroup of  ; it is always connected. Any two maximal tori of
; it is always connected. Any two maximal tori of 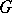 are conjugate in
are conjugate in  . If
. If  is defined over a field
is defined over a field 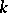 , then there is a maximal torus in
, then there is a maximal torus in 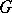 also defined over
also defined over 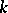 ; its centralizer is also defined over
; its centralizer is also defined over  .
.
Let 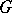 be a reductive group defined over a field
be a reductive group defined over a field 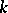 . Consider the maximal subgroups among all algebraic subgroups of
. Consider the maximal subgroups among all algebraic subgroups of 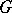 which are
which are 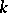 -split algebraic tori. The maximal
-split algebraic tori. The maximal 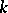 -split tori thus obtained are conjugate over
-split tori thus obtained are conjugate over 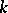 . The common dimension of these tori is called the
. The common dimension of these tori is called the  -rank of
-rank of 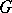 and is denoted by
and is denoted by 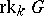 . A maximal
. A maximal 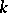 -split torus need not, in general, be a maximal torus, that is,
-split torus need not, in general, be a maximal torus, that is, 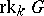 is in general less than the rank of
is in general less than the rank of 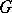 (which is equal to the dimension of a maximal torus in
(which is equal to the dimension of a maximal torus in 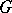 ). If
). If 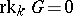 , then
, then 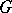 is called an anisotropic group over
is called an anisotropic group over 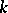 , and if
, and if 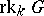 coincides with the rank of
coincides with the rank of 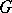 , then
, then 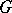 is called a split group over
is called a split group over 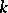 . If
. If 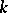 is algebraically closed, then
is algebraically closed, then 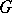 is always split over
is always split over 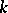 . In general,
. In general,  is split over the separable closure of
is split over the separable closure of 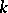 .
.
Examples. Let 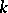 be a field and let
be a field and let 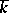 be an algebraic closure. The group
be an algebraic closure. The group  of non-singular matrices of order
of non-singular matrices of order  with coefficients in
with coefficients in 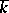 (see Classical group; General linear group) is defined and split over the prime subfield of
(see Classical group; General linear group) is defined and split over the prime subfield of 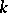 . The subgroup of all diagonal matrices is a maximal torus in
. The subgroup of all diagonal matrices is a maximal torus in  .
.
Let the characteristic of 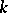 be different from 2. Let
be different from 2. Let 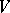 be an
be an  -dimensional vector space over
-dimensional vector space over 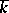 and
and 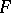 a non-degenerate quadratic form on
a non-degenerate quadratic form on 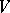 defined over
defined over 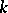 (the latter means that in some basis
(the latter means that in some basis  of
of 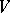 , the form
, the form  is a polynomial in
is a polynomial in  with coefficients in
with coefficients in 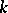 ). Let
). Let 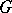 be the group of all non-singular linear transformations of
be the group of all non-singular linear transformations of 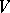 with determinant 1 and preserving
with determinant 1 and preserving 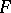 . It is defined over
. It is defined over 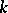 . Let
. Let  be the linear hull over
be the linear hull over 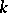 of
of  ; it is a
; it is a 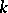 -form of
-form of 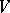 . In
. In 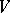 there always exists a basis
there always exists a basis 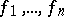 such that
such that
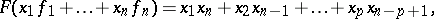 |
where 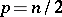 if
if  is even and
is even and 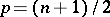 if
if  is odd. The subgroup of
is odd. The subgroup of 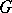 consisting of the elements whose matrix in this basis takes the form
consisting of the elements whose matrix in this basis takes the form 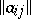 , where
, where 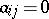 for
for 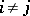 and
and 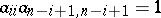 for
for 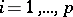 , is a maximal torus in
, is a maximal torus in  (thus the rank of
(thus the rank of  is equal to the integer part of
is equal to the integer part of 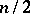 ). In general, this basis does not belong to
). In general, this basis does not belong to  . However, there always is a basis
. However, there always is a basis 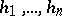 in
in 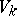 in which the quadratic form can be written as
in which the quadratic form can be written as
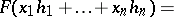 |
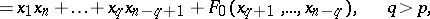 |
where 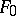 is a quadratic form which is anisotropic over
is a quadratic form which is anisotropic over 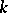 (that is, the equation
(that is, the equation 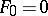 only has the zero solution in
only has the zero solution in 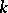 , see Witt decomposition). The subgroup of
, see Witt decomposition). The subgroup of 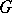 consisting of the elements whose matrix in the basis
consisting of the elements whose matrix in the basis  takes the form
takes the form 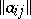 , where
, where 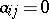 for
for 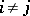 ,
, 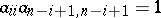 for
for 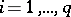 and
and 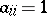 for
for 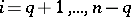 , is a maximal
, is a maximal 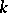 -split torus in
-split torus in 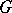 (so
(so 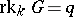 and
and  is split if and only if
is split if and only if 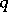 is the integer part of
is the integer part of 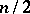 ).
).
Using maximal tori one associates to a reductive group 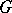 a root system, which is a basic ingredient for the classification of reductive groups. Namely, let
a root system, which is a basic ingredient for the classification of reductive groups. Namely, let 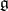 be the Lie algebra of
be the Lie algebra of 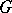 and let
and let 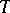 be a fixed maximal torus in
be a fixed maximal torus in  . The adjoint representation of
. The adjoint representation of 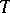 in
in 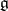 is rational and diagonalizable, so
is rational and diagonalizable, so 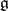 decomposes into a direct sum of weight spaces for this representation. The set of non-zero weights of this representation (considered as a subset of its linear hull in the vector space
decomposes into a direct sum of weight spaces for this representation. The set of non-zero weights of this representation (considered as a subset of its linear hull in the vector space 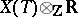 , where
, where 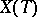 is the group of rational characters of
is the group of rational characters of  ) turns out to be a (reduced) root system. The relative root system is defined in a similar way: If
) turns out to be a (reduced) root system. The relative root system is defined in a similar way: If 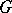 is defined over
is defined over 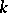 and
and 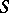 is a maximal
is a maximal 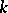 -split torus in
-split torus in 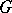 , then the set of non-zero weights of the adjoint representation of
, then the set of non-zero weights of the adjoint representation of 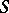 in
in 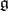 forms a root system (which need not be reduced) in some subspace of
forms a root system (which need not be reduced) in some subspace of 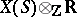 . See also Weyl group; Semi-simple group.
. See also Weyl group; Semi-simple group.
References
| [1] | A. Borel, "Linear algebraic groups" , Benjamin (1969) MR0251042 Zbl 0206.49801 Zbl 0186.33201 |
| [2] | A. Borel (ed.) G.D. Mostow (ed.) , Algebraic groups and discontinuous subgroups , Proc. Symp. Pure Math. , 9 , Amer. Math. Soc. (1966) MR0202512 Zbl 0171.24105 |
Comments
For 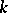 -forms see Form of an (algebraic) structure.
-forms see Form of an (algebraic) structure.
See especially the article by A. Borel in [2].
A maximal torus of a connected real Lie group 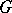 is a connected compact commutative Lie subgroup
is a connected compact commutative Lie subgroup 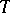 of
of 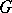 not contained in any larger subgroup of the same type. As a Lie group
not contained in any larger subgroup of the same type. As a Lie group 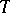 is isomorphic to a direct product of copies of the multiplicative group of complex numbers of absolute value 1. Every maximal torus of
is isomorphic to a direct product of copies of the multiplicative group of complex numbers of absolute value 1. Every maximal torus of 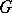 is contained in a maximal compact subgroup of
is contained in a maximal compact subgroup of 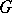 ; any two maximal tori of
; any two maximal tori of  (as any two maximal compact subgroups) are conjugate in
(as any two maximal compact subgroups) are conjugate in 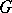 . This, in a well-known sense, reduces the study of maximal tori to the case when
. This, in a well-known sense, reduces the study of maximal tori to the case when 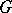 is compact.
is compact.
Now let 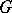 be a compact group. The union of all maximal tori of
be a compact group. The union of all maximal tori of 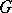 is
is 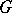 and their intersection is the centre of
and their intersection is the centre of  . The Lie algebra of a maximal torus
. The Lie algebra of a maximal torus  is a maximal commutative subalgebra in the Lie algebra
is a maximal commutative subalgebra in the Lie algebra 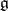 of
of 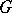 , and each maximal commutative subalgebra in
, and each maximal commutative subalgebra in 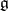 can be obtained in this way. The centralizer of a maximal torus
can be obtained in this way. The centralizer of a maximal torus 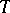 in
in 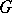 coincides with
coincides with 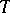 . The adjoint representation of
. The adjoint representation of 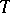 in
in 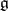 is diagonalizable and all non-zero weights of this representation form a root system in
is diagonalizable and all non-zero weights of this representation form a root system in 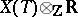 , where
, where  is the group of characters of
is the group of characters of  . This is a basic ingredient for the classification of compact Lie groups.
. This is a basic ingredient for the classification of compact Lie groups.
References
| [1] | L.S. Pontryagin, "Topological groups" , Princeton Univ. Press (1958) (Translated from Russian) MR0201557 Zbl 0022.17104 |
| [2] | D.P. Zhelobenko, "Compact Lie groups and their representations" , Amer. Math. Soc. (1973) (Translated from Russian) MR0473097 MR0473098 Zbl 0228.22013 |
| [3] | S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978) MR0514561 Zbl 0451.53038 |
Comments
References
| [a1] | N. Bourbaki, "Groupes et algèbres de Lie" , Eléments de mathématiques , Masson (1982) pp. Chapt. 9. Groupes de Lie réels compacts MR0682756 Zbl 0505.22006 |
| [a2] | Th. Bröcker, T. Tom Dieck, "Representations of compact Lie groups" , Springer (1985) MR0781344 Zbl 0581.22009 |
Maximal torus. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximal_torus&oldid=16122