Difference between revisions of "Measure-preserving transformation"
(Importing text file) |
(MSC|28D05 Category:Measure-theoretic ergodic theory) |
||
| Line 1: | Line 1: | ||
''of a [[Measure space|measure space]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063270/m0632701.png" />.'' | ''of a [[Measure space|measure space]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063270/m0632701.png" />.'' | ||
| + | |||
| + | {{MSC|28D05}} | ||
| + | |||
| + | [[Category:Measure-theoretic ergodic theory]] | ||
A [[Measurable mapping|measurable mapping]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063270/m0632702.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063270/m0632703.png" /> for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063270/m0632704.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063270/m0632705.png" /> is called an invariant measure for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063270/m0632706.png" />. A measurable mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063270/m0632707.png" /> between measure spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063270/m0632708.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063270/m0632709.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063270/m06327010.png" /> for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063270/m06327011.png" /> is usually called a measure-preserving mapping. A surjective measure-preserving transformation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063270/m06327012.png" /> of a measure space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063270/m06327013.png" />, i.e., <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063270/m06327014.png" /> maps <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063270/m06327015.png" /> onto itself, is often called an endomorphism of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063270/m06327016.png" />; an endomorphism which is bijective and whose inverse is also measure preserving is called an [[Automorphism|automorphism]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063270/m06327017.png" />. | A [[Measurable mapping|measurable mapping]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063270/m0632702.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063270/m0632703.png" /> for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063270/m0632704.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063270/m0632705.png" /> is called an invariant measure for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063270/m0632706.png" />. A measurable mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063270/m0632707.png" /> between measure spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063270/m0632708.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063270/m0632709.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063270/m06327010.png" /> for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063270/m06327011.png" /> is usually called a measure-preserving mapping. A surjective measure-preserving transformation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063270/m06327012.png" /> of a measure space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063270/m06327013.png" />, i.e., <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063270/m06327014.png" /> maps <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063270/m06327015.png" /> onto itself, is often called an endomorphism of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063270/m06327016.png" />; an endomorphism which is bijective and whose inverse is also measure preserving is called an [[Automorphism|automorphism]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063270/m06327017.png" />. | ||
Revision as of 19:16, 18 March 2012
of a measure space  .
.
2020 Mathematics Subject Classification: Primary: 28D05 [MSN][ZBL]
A measurable mapping  such that
such that  for every
for every  ;
;  is called an invariant measure for
is called an invariant measure for  . A measurable mapping
. A measurable mapping  between measure spaces
between measure spaces  and
and  such that
such that  for every
for every  is usually called a measure-preserving mapping. A surjective measure-preserving transformation
is usually called a measure-preserving mapping. A surjective measure-preserving transformation 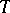 of a measure space
of a measure space 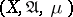 , i.e.,
, i.e., 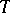 maps
maps 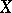 onto itself, is often called an endomorphism of
onto itself, is often called an endomorphism of  ; an endomorphism which is bijective and whose inverse is also measure preserving is called an automorphism of
; an endomorphism which is bijective and whose inverse is also measure preserving is called an automorphism of 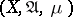 .
.
Measure-preserving transformations arise, for example, in the study of classical dynamical systems (cf. (measurable) Cascade; Measurable flow). In that case the transformation is first obtained as a continuous (or smooth) transformation of some, often compact, topological space (or manifold), and the existence of an invariant measure is proved. An example is Liouville's theorem for a Hamiltonian system (cf. also Liouville theorems).
For further information and references see Ergodic theory.
Measure-preserving transformation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Measure-preserving_transformation&oldid=15953