Difference between revisions of "Omega-completeness"
From Encyclopedia of Mathematics
(Importing text file) |
(TeX) |
||
| Line 1: | Line 1: | ||
| − | '' | + | {{TEX|done}} |
| + | ''$\omega$-completeness'' | ||
| − | The property of formal systems of arithmetic in which, for any formula | + | The property of formal systems of arithmetic in which, for any formula $A(x)$, from a deduction of $A(\bar0),\ldots,A(\bar n),\ldots,$ it follows that one can infer the formula $\forall xA(x)$, where $\bar n$ is a constant signifying the natural number $n$. If this is not true, the system is called <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068150/o0681509.png" />-incomplete. K. Gödel in his incompleteness theorem (cf. [[Gödel incompleteness theorem|Gödel incompleteness theorem]]) actually established the $\omega$-incompleteness of formal arithmetic. If all formulas which are true in the standard model of arithmetic are taken as axioms, then an $\omega$-complete axiom system is obtained. On the other hand, in every $\omega$-complete extension of Peano arithmetic, every formula which is true in the standard model can be deduced. |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> S.C. Kleene, "Introduction to metamathematics" , North-Holland (1951)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> S.C. Kleene, "Introduction to metamathematics" , North-Holland (1951)</TD></TR></table> | ||
Revision as of 13:40, 9 April 2014
$\omega$-completeness
The property of formal systems of arithmetic in which, for any formula $A(x)$, from a deduction of $A(\bar0),\ldots,A(\bar n),\ldots,$ it follows that one can infer the formula $\forall xA(x)$, where $\bar n$ is a constant signifying the natural number $n$. If this is not true, the system is called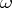 
-incomplete. K. Gödel in his incompleteness theorem (cf. Gödel incompleteness theorem) actually established the $\omega$-incompleteness of formal arithmetic. If all formulas which are true in the standard model of arithmetic are taken as axioms, then an $\omega$-complete axiom system is obtained. On the other hand, in every $\omega$-complete extension of Peano arithmetic, every formula which is true in the standard model can be deduced.
References
| [1] | S.C. Kleene, "Introduction to metamathematics" , North-Holland (1951) |
How to Cite This Entry:
Omega-completeness. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Omega-completeness&oldid=15799
Omega-completeness. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Omega-completeness&oldid=15799
This article was adapted from an original article by V.N. Grishin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article