Difference between revisions of "Quantum Grassmannian"
(Importing text file) |
m (AUTOMATIC EDIT (latexlist): Replaced 54 formulas out of 56 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 56 formulas, 54 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|partial}} | |
| + | A subalgebra $\mathcal{G} = \operatorname { Fun } _ { q } ( G ( k , n ) )$ in the algebra $\mathcal{A} = \operatorname { Fun } _ { q } ( \operatorname{SL} ( n , \mathbf{C} ) )$ of regular functions on the quantum group $\operatorname{SL} ( n , \mathbf{C} )$ (cf. [[Quantum groups|Quantum groups]]). $\mathcal{G}$ is generated by quantum minors $| T _ { i _ { 1 } , \ldots , i _ { k } } ^ { 1 , \ldots , k } | _ { q }$, with $1 \leq i _ { 1 } < \ldots < i _ { k } \leq n$ and with $T \in \operatorname { Mat } ( n ) \otimes \mathcal{A}$ the vector co-representation of $\mathcal{A}$ [[#References|[a1]]]. The $q$-minors satisfy quadratic relations, which turn into the Plücker relations (Young symmetries, cf. also [[Grassmann manifold|Grassmann manifold]]) when the deformation parameter $q$ is specialized to $1$. Since classically the Grassmannian, as a complex submanifold in the projective space $\mathbf{P} ( \wedge ^ { k } \mathbf{C} ^ { n } )$, is the common zero locus of the Plücker relations, one interprets $\mathcal{G}$ as a quantization of the complex Poisson manifold $G ( k , n )$ (cf. [[Symplectic structure|Symplectic structure]]). The co-multiplication $\Delta$ in $\mathcal{A}$ induces a right co-action $R = \Delta |_{\cal G} :\cal G \rightarrow G \otimes A$ and so $\mathcal{G}$ is a [[Quantum homogeneous space|quantum homogeneous space]]. | ||
| − | + | A more general construction of (generalized) quantum flag manifolds exists for the group $\operatorname{SL} ( n , \mathbf{C} )$ [[#References|[a1]]], as well as for other simple complex Lie groups $G$ having quantum counterparts [[#References|[a2]]]. Another description was given in [[#References|[a3]]]. Both approaches [[#References|[a2]]], [[#References|[a3]]] also allow one to define quantum Schubert varieties. | |
| − | + | Since $G ( k , n )$ is compact, the only holomorphic functions defined globally on it are the constants. But one can work instead with holomorphic coordinates $z _ { s t }$, $1 \leq s \leq k$, $1 \leq t \leq n - k$, on the big cell $C$, the unique Schubert cell of top dimension. The standard choice of coordinates is given via the Gauss decomposition of $T$. For the algebra $\mathcal{G}$ this means in fact a localization by allowing the $q$-minor $| T _ { 1, \dots, k } ^ { 1 , \ldots , k } | _ { q }$ to be invertible. The generators $z _ { s t }$ of the quantum big cell $\mathcal{C} = \operatorname { Fun } _ { q } ( C )$ satisfy the relations [[#References|[a4]]] | |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120020/q12002032.png"/></td> </tr></table> |
| − | + | The [[Symplectic manifold|symplectic manifold]] $G ( k , n )$ can be realized as an orbit of the dressing transformation of $\operatorname{SU} ( n )$ acting on its dual [[Poisson Lie group|Poisson Lie group]]. The transformation can be also viewed as the right $\operatorname{SU} ( n )$-action on the manifold $M$ of $( n \times n )$ unimodular positive matrices: $( m , u ) \mapsto u ^ { * } m u$. The orbits are determined by sets of eigenvalues and $G ( k , n )$ corresponds to a two-point set $\{ \lambda _ { 1 } , \lambda _ { 2 } \}$ with multiplicities $k$ and $n - k$, respectively. There exists a quantum analogue as a right co-action | |
| − | Similarly as for quantum spheres (cf. [[Quantum sphere|Quantum sphere]]), other types of quantum Grassmannians have been defined, distinguished by possessing classical points, i.e., one-dimensional representations | + | \begin{equation*} \operatorname { Fun } _ { q } ( M ) \rightarrow \operatorname { Fun } _ { q } ( M ) \bigotimes \operatorname { Fun } _ { q } ( \operatorname {SU} ( n ) ). \end{equation*} |
| + | |||
| + | $\operatorname { Fun } _ { q } ( M )$ is endowed with a $*$-involution and, correspondingly, one can turn $\mathcal{C}$ into a $*$-algebra by determining the commutation relations between $z _ { s t }$ and $z ^ { * _{ u v}}$ in dependence on the parameters $\lambda _ { 1 }$ and $\lambda _ { 2 }$ [[#References|[a4]]]. | ||
| + | |||
| + | Similarly as for quantum spheres (cf. [[Quantum sphere|Quantum sphere]]), other types of quantum Grassmannians have been defined, distinguished by possessing classical points, i.e., one-dimensional representations $\operatorname {Fun}_q ( G ( k , n ) ) \rightarrow \mathbf C $ [[#References|[a5]]]. | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> E. Taft, J. Towber, "Quantum deformations of flag schemes and Grassmann schemes I. A $q$-deformation for the shape algebra $\operatorname{GL} ( n )$" ''J. Algebra'' , '''142''' (1991) pp. 1–36</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> Ya.S. Soibelman, "On the quantum flag manifold" ''Funct. Anal. Appl.'' , '''26''' (1992) pp. 225–227</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> V. Lakshmibai, N. Reshetikhin, "Quantum deformations of flag and Schubert schemes" ''C.R. Acad. Sci. Paris'' , '''313''' (1991) pp. 121–126</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> P. Šťovíček, "Quantum Grassmann manifolds" ''Comm. Math. Phys.'' , '''158''' (1993) pp. 135–153</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> M. Nuomi, M.S. Dijkhuizen, T. Sugitani, "Multivariable Askey–Wilson polynomials and quantum complex Grassmannians" M.E.H. Insmail (ed.) et al. (ed.) , ''Special Functions, $q$-Series and Related Topics'' , ''Fields Inst. Commun.'' , '''14''' , Amer. Math. Soc. (1997) pp. 167–177</td></tr></table> |
Revision as of 16:56, 1 July 2020
A subalgebra $\mathcal{G} = \operatorname { Fun } _ { q } ( G ( k , n ) )$ in the algebra $\mathcal{A} = \operatorname { Fun } _ { q } ( \operatorname{SL} ( n , \mathbf{C} ) )$ of regular functions on the quantum group $\operatorname{SL} ( n , \mathbf{C} )$ (cf. Quantum groups). $\mathcal{G}$ is generated by quantum minors $| T _ { i _ { 1 } , \ldots , i _ { k } } ^ { 1 , \ldots , k } | _ { q }$, with $1 \leq i _ { 1 } < \ldots < i _ { k } \leq n$ and with $T \in \operatorname { Mat } ( n ) \otimes \mathcal{A}$ the vector co-representation of $\mathcal{A}$ [a1]. The $q$-minors satisfy quadratic relations, which turn into the Plücker relations (Young symmetries, cf. also Grassmann manifold) when the deformation parameter $q$ is specialized to $1$. Since classically the Grassmannian, as a complex submanifold in the projective space $\mathbf{P} ( \wedge ^ { k } \mathbf{C} ^ { n } )$, is the common zero locus of the Plücker relations, one interprets $\mathcal{G}$ as a quantization of the complex Poisson manifold $G ( k , n )$ (cf. Symplectic structure). The co-multiplication $\Delta$ in $\mathcal{A}$ induces a right co-action $R = \Delta |_{\cal G} :\cal G \rightarrow G \otimes A$ and so $\mathcal{G}$ is a quantum homogeneous space.
A more general construction of (generalized) quantum flag manifolds exists for the group $\operatorname{SL} ( n , \mathbf{C} )$ [a1], as well as for other simple complex Lie groups $G$ having quantum counterparts [a2]. Another description was given in [a3]. Both approaches [a2], [a3] also allow one to define quantum Schubert varieties.
Since $G ( k , n )$ is compact, the only holomorphic functions defined globally on it are the constants. But one can work instead with holomorphic coordinates $z _ { s t }$, $1 \leq s \leq k$, $1 \leq t \leq n - k$, on the big cell $C$, the unique Schubert cell of top dimension. The standard choice of coordinates is given via the Gauss decomposition of $T$. For the algebra $\mathcal{G}$ this means in fact a localization by allowing the $q$-minor $| T _ { 1, \dots, k } ^ { 1 , \ldots , k } | _ { q }$ to be invertible. The generators $z _ { s t }$ of the quantum big cell $\mathcal{C} = \operatorname { Fun } _ { q } ( C )$ satisfy the relations [a4]
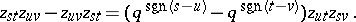 |
The symplectic manifold $G ( k , n )$ can be realized as an orbit of the dressing transformation of $\operatorname{SU} ( n )$ acting on its dual Poisson Lie group. The transformation can be also viewed as the right $\operatorname{SU} ( n )$-action on the manifold $M$ of $( n \times n )$ unimodular positive matrices: $( m , u ) \mapsto u ^ { * } m u$. The orbits are determined by sets of eigenvalues and $G ( k , n )$ corresponds to a two-point set $\{ \lambda _ { 1 } , \lambda _ { 2 } \}$ with multiplicities $k$ and $n - k$, respectively. There exists a quantum analogue as a right co-action
\begin{equation*} \operatorname { Fun } _ { q } ( M ) \rightarrow \operatorname { Fun } _ { q } ( M ) \bigotimes \operatorname { Fun } _ { q } ( \operatorname {SU} ( n ) ). \end{equation*}
$\operatorname { Fun } _ { q } ( M )$ is endowed with a $*$-involution and, correspondingly, one can turn $\mathcal{C}$ into a $*$-algebra by determining the commutation relations between $z _ { s t }$ and $z ^ { * _{ u v}}$ in dependence on the parameters $\lambda _ { 1 }$ and $\lambda _ { 2 }$ [a4].
Similarly as for quantum spheres (cf. Quantum sphere), other types of quantum Grassmannians have been defined, distinguished by possessing classical points, i.e., one-dimensional representations $\operatorname {Fun}_q ( G ( k , n ) ) \rightarrow \mathbf C $ [a5].
References
| [a1] | E. Taft, J. Towber, "Quantum deformations of flag schemes and Grassmann schemes I. A $q$-deformation for the shape algebra $\operatorname{GL} ( n )$" J. Algebra , 142 (1991) pp. 1–36 |
| [a2] | Ya.S. Soibelman, "On the quantum flag manifold" Funct. Anal. Appl. , 26 (1992) pp. 225–227 |
| [a3] | V. Lakshmibai, N. Reshetikhin, "Quantum deformations of flag and Schubert schemes" C.R. Acad. Sci. Paris , 313 (1991) pp. 121–126 |
| [a4] | P. Šťovíček, "Quantum Grassmann manifolds" Comm. Math. Phys. , 158 (1993) pp. 135–153 |
| [a5] | M. Nuomi, M.S. Dijkhuizen, T. Sugitani, "Multivariable Askey–Wilson polynomials and quantum complex Grassmannians" M.E.H. Insmail (ed.) et al. (ed.) , Special Functions, $q$-Series and Related Topics , Fields Inst. Commun. , 14 , Amer. Math. Soc. (1997) pp. 167–177 |
Quantum Grassmannian. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quantum_Grassmannian&oldid=15744