Difference between revisions of "Tate module"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 10: | Line 10: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> J.T. Tate, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227061.png" />-divisible groups" T.A. Springer (ed.) et al. (ed.) , ''Proc. Conf. local fields (Driebergen, 1966)'' , Springer (1967) pp. 158–183 {{MR|0231827}} {{ZBL|0157.27601}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> I.R. Shafarevich, "The zeta-function" , Moscow (1969) (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> K. Iwasawa, "On the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227062.png" />-invariants of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227063.png" />-extensions" , ''Number theory, algebraic geometry and commutative algebra'' , Kinokuniya (1973) pp. 1–11 {{MR|357371}} {{ZBL|}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> B. Ferrero, L.C. Washington, "The Iwasawa invariant <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227064.png" /> vanishes for abelian number fields" ''Ann. of Math.'' , '''109''' (1979) pp. 377–395 {{MR|528968}} {{ZBL|0443.12001}} </TD></TR></table> |
Revision as of 21:57, 30 March 2012
A free  -module
-module  associated to a
associated to a  -divisible group
-divisible group  defined over a complete discrete valuation ring
defined over a complete discrete valuation ring  of characteristic 0 with residue field
of characteristic 0 with residue field  of characteristic
of characteristic  . Let
. Let  ,
,  , and
, and 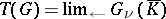 , where
, where  is the algebraic closure of the quotient field
is the algebraic closure of the quotient field 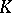 of the ring
of the ring 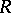 ; the limit is taken with respect to the mappings
; the limit is taken with respect to the mappings 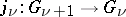 for which
for which 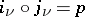 . Then
. Then  , where
, where 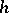 is the height of the group
is the height of the group 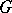 and
and  has the natural structure of a
has the natural structure of a 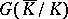 -module. The functor
-module. The functor 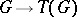 allows one to reduce a number of questions about the group
allows one to reduce a number of questions about the group  to simpler questions about
to simpler questions about  -modules.
-modules.
The Tate module is defined similarly for an Abelian variety. Let  be an Abelian variety defined over
be an Abelian variety defined over  , and let
, and let 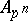 be the group of points of order
be the group of points of order  in
in  . Then
. Then  is defined as
is defined as  . The Tate module of a curve
. The Tate module of a curve 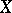 is the Tate module of its Jacobi variety.
is the Tate module of its Jacobi variety.
The construction of the module  can be extended to number fields. Let
can be extended to number fields. Let  be an algebraic number field and let
be an algebraic number field and let  be a
be a  -extension of the field
-extension of the field  (an extension with Galois group isomorphic to
(an extension with Galois group isomorphic to 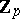 ). For the intermediate field
). For the intermediate field  of degree
of degree  over
over 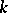 , let
, let  be the
be the 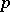 -component of the ideal class group of the field
-component of the ideal class group of the field 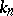 . Then
. Then  , where the limit is taken with respect to norm-mappings
, where the limit is taken with respect to norm-mappings  for
for 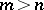 . The module
. The module 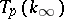 is characterized by its Iwasawa invariants
is characterized by its Iwasawa invariants 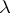 ,
, 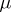 and
and  , defined by
, defined by
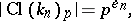 |
where  for all sufficiently large
for all sufficiently large  . For cyclotomic
. For cyclotomic  -extensions the invariant
-extensions the invariant  is equal to 0. This was also proved for Abelian fields [4]. Examples are known of non-cyclotomic
is equal to 0. This was also proved for Abelian fields [4]. Examples are known of non-cyclotomic 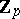 -extensions with
-extensions with  (see [3]). Even in the case when
(see [3]). Even in the case when  ,
, 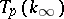 is not necessarily a free
is not necessarily a free 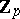 -module.
-module.
References
| [1] | J.T. Tate, "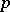 -divisible groups" T.A. Springer (ed.) et al. (ed.) , Proc. Conf. local fields (Driebergen, 1966) , Springer (1967) pp. 158–183 MR0231827 Zbl 0157.27601 -divisible groups" T.A. Springer (ed.) et al. (ed.) , Proc. Conf. local fields (Driebergen, 1966) , Springer (1967) pp. 158–183 MR0231827 Zbl 0157.27601 |
| [2] | I.R. Shafarevich, "The zeta-function" , Moscow (1969) (In Russian) |
| [3] | K. Iwasawa, "On the 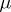 -invariants of -invariants of 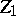 -extensions" , Number theory, algebraic geometry and commutative algebra , Kinokuniya (1973) pp. 1–11 MR357371 -extensions" , Number theory, algebraic geometry and commutative algebra , Kinokuniya (1973) pp. 1–11 MR357371 |
| [4] | B. Ferrero, L.C. Washington, "The Iwasawa invariant 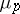 vanishes for abelian number fields" Ann. of Math. , 109 (1979) pp. 377–395 MR528968 Zbl 0443.12001 vanishes for abelian number fields" Ann. of Math. , 109 (1979) pp. 377–395 MR528968 Zbl 0443.12001 |
Tate module. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tate_module&oldid=14732