Difference between revisions of "Symmetric difference of sets"
From Encyclopedia of Mathematics
(Importing text file) |
m (links) |
||
| Line 8: | Line 8: | ||
====Comments==== | ====Comments==== | ||
| − | The symmetric difference operation is associative, i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091640/s0916409.png" />, and intersection is distributive over it, i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091640/s09164010.png" />. Thus, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091640/s09164011.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091640/s09164012.png" /> define a ring structure on the power set of a set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091640/s09164013.png" /> (the set of subsets of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091640/s09164014.png" />), in contrast to union and intersection. This ring is the same as the ring of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091640/s09164015.png" />-valued functions on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091640/s09164016.png" /> (with pointwise multiplication and addition). Cf. also [[ | + | The symmetric difference operation is associative, i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091640/s0916409.png" />, and intersection is distributive over it, i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091640/s09164010.png" />. Thus, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091640/s09164011.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091640/s09164012.png" /> define a ring structure on the power set of a set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091640/s09164013.png" /> (the set of subsets of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091640/s09164014.png" />), in contrast to union and intersection. This ring is the same as the ring of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091640/s09164015.png" />-valued functions on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091640/s09164016.png" /> (with [[pointwise multiplication]] and addition). Cf. also [[Boolean algebra]] and [[Boolean ring]] for the symmetric difference operation in an arbitrary Boolean algebra. |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> C. Kuratowski, "Introduction to set theory and topology" , Pergamon (1961) pp. 34, 35 (Translated from French)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> C. Kuratowski, "Introduction to set theory and topology" , Pergamon (1961) pp. 34, 35 (Translated from French)</TD></TR></table> | ||
Revision as of 18:19, 1 December 2014
An operation on sets. Given two sets 
and 
, their symmetric difference, denoted by 
, is given by
 |
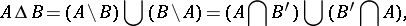where the symbols 
, 
, 
, 
denote the operations of union, intersection, difference, and complementation of sets, respectively.
Comments
The symmetric difference operation is associative, i.e. 
, and intersection is distributive over it, i.e.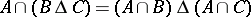 
. Thus, 
and 
define a ring structure on the power set of a set 
(the set of subsets of 
), in contrast to union and intersection. This ring is the same as the ring of 
-valued functions on 
(with pointwise multiplication and addition). Cf. also Boolean algebra and Boolean ring for the symmetric difference operation in an arbitrary Boolean algebra.
References
| [a1] | C. Kuratowski, "Introduction to set theory and topology" , Pergamon (1961) pp. 34, 35 (Translated from French) |
How to Cite This Entry:
Symmetric difference of sets. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Symmetric_difference_of_sets&oldid=14687
Symmetric difference of sets. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Symmetric_difference_of_sets&oldid=14687
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article