Difference between revisions of "Step hyperbolic cross"
From Encyclopedia of Mathematics
(Importing text file) |
m (AUTOMATIC EDIT (latexlist): Replaced 20 formulas out of 22 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 22 formulas, 20 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|partial}} | |
| + | A summation domain of multiple [[Fourier series|Fourier series]]. Like a [[Hyperbolic cross|hyperbolic cross]], it is used for good approximation in the space of functions with bounded mixed derivative (in $L _ { p }$). | ||
| − | <table class="eq" style="width:100%;"> <tr><td | + | Let $f ( x )$ be an integrable periodic function of $n$ variables defined on $\mathbf{T} ^ { n }$. It has a Fourier series expansion $\sum _ { \mathbf{k} } c_{ \mathbf{k} } e ^ { i \mathbf{kx} }$, $\mathbf{k} = ( k _ { 1 } , \dots , k _ { n } )$, ${\bf x} = ( x _ { 1 } , \ldots , x _ { n } )$, $\mathbf{k} \cdot \mathbf{x} = k _ { 1 } x _ { 1 } + \ldots + k _ { n } x _ { n }$. Unlike in the one-dimensional case, there is no natural ordering of the Fourier coefficients, so the choice of the order of summation is of great importance. |
| + | |||
| + | Let $\mathbf{r} = ( r _ { 1 } , \dots , r _ { n } ) \in \mathbf{R} ^ { n }$ with all coordinates positive, $r_j > 0$. Let | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130570/s13057011.png"/></td> </tr></table> | ||
be a dyadic "block" of the Fourier series. The step hyperbolic partial sums | be a dyadic "block" of the Fourier series. The step hyperbolic partial sums | ||
| − | + | \begin{equation*} \sum _ { |\mathbf{m \cdot r}| \leq N } \Delta _ { \mathbf{m} } (\, f ) \end{equation*} | |
| − | where introduced by B. Mityagin [[#References|[a2]]] for problems in [[Approximation theory|approximation theory]]. They have approximately the same number of harmonics as a hyperbolic cross, but structurally they fit the Marcinkiewicz multiplier theorem (cf. also [[Interpolation of operators|Interpolation of operators]]). It implies that the operator of taking step hyperbolic partial Fourier sums is bounded in each | + | where introduced by B. Mityagin [[#References|[a2]]] for problems in [[Approximation theory|approximation theory]]. They have approximately the same number of harmonics as a hyperbolic cross, but structurally they fit the Marcinkiewicz multiplier theorem (cf. also [[Interpolation of operators|Interpolation of operators]]). It implies that the operator of taking step hyperbolic partial Fourier sums is bounded in each $L ^ { p }$, $1 < p < \infty$. This means that step hyperbolic partial sums give the best approximation among all hyperbolic cross trigonometric polynomials in $L _ { p }$, $1 < p < \infty$. In the limit cases $p = 1$ and $p = \infty$, the [[Lebesgue constants|Lebesgue constants]] of step hyperbolic partial sums have only logarithmic growth, while for hyperbolic partial Fourier sums they grow as a power of $N$. |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> E.S. Belinsky, "Lebesgue constants of "step-hyperbolic" partial sums" , ''Theory of Functions and Mappings'' , Nauk. Dumka, Kiev (1989) (In Russian)</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> B.S. Mityagin, "Approximation of functions in $L ^ { p }$ and $C$ spaces on the torus" ''Mat. Sb. (N.S.)'' , '''58 (100)''' (1962) pp. 397–414 (In Russian)</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> V. Temlyakov, "Approximation of periodic functions" , Nova Sci. (1993)</td></tr></table> |
Revision as of 16:57, 1 July 2020
A summation domain of multiple Fourier series. Like a hyperbolic cross, it is used for good approximation in the space of functions with bounded mixed derivative (in $L _ { p }$).
Let $f ( x )$ be an integrable periodic function of $n$ variables defined on $\mathbf{T} ^ { n }$. It has a Fourier series expansion $\sum _ { \mathbf{k} } c_{ \mathbf{k} } e ^ { i \mathbf{kx} }$, $\mathbf{k} = ( k _ { 1 } , \dots , k _ { n } )$, ${\bf x} = ( x _ { 1 } , \ldots , x _ { n } )$, $\mathbf{k} \cdot \mathbf{x} = k _ { 1 } x _ { 1 } + \ldots + k _ { n } x _ { n }$. Unlike in the one-dimensional case, there is no natural ordering of the Fourier coefficients, so the choice of the order of summation is of great importance.
Let $\mathbf{r} = ( r _ { 1 } , \dots , r _ { n } ) \in \mathbf{R} ^ { n }$ with all coordinates positive, $r_j > 0$. Let
 |
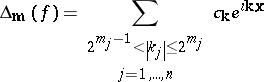be a dyadic "block" of the Fourier series. The step hyperbolic partial sums
\begin{equation*} \sum _ { |\mathbf{m \cdot r}| \leq N } \Delta _ { \mathbf{m} } (\, f ) \end{equation*}
where introduced by B. Mityagin [a2] for problems in approximation theory. They have approximately the same number of harmonics as a hyperbolic cross, but structurally they fit the Marcinkiewicz multiplier theorem (cf. also Interpolation of operators). It implies that the operator of taking step hyperbolic partial Fourier sums is bounded in each $L ^ { p }$, $1 < p < \infty$. This means that step hyperbolic partial sums give the best approximation among all hyperbolic cross trigonometric polynomials in $L _ { p }$, $1 < p < \infty$. In the limit cases $p = 1$ and $p = \infty$, the Lebesgue constants of step hyperbolic partial sums have only logarithmic growth, while for hyperbolic partial Fourier sums they grow as a power of $N$.
References
| [a1] | E.S. Belinsky, "Lebesgue constants of "step-hyperbolic" partial sums" , Theory of Functions and Mappings , Nauk. Dumka, Kiev (1989) (In Russian) |
| [a2] | B.S. Mityagin, "Approximation of functions in $L ^ { p }$ and $C$ spaces on the torus" Mat. Sb. (N.S.) , 58 (100) (1962) pp. 397–414 (In Russian) |
| [a3] | V. Temlyakov, "Approximation of periodic functions" , Nova Sci. (1993) |
How to Cite This Entry:
Step hyperbolic cross. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Step_hyperbolic_cross&oldid=14671
Step hyperbolic cross. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Step_hyperbolic_cross&oldid=14671
This article was adapted from an original article by E.S. Belinsky (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article