Cartesian-closed category

A category such that the following axioms are satisfied:

A1) there exists a terminal object ;

A2) for any pair , of objects of there exist a product and given projections , ;

A3) for any pair , of objects of there exist an object 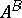and an evaluation arrow such that for any arrow there is a unique arrow 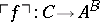with .

These conditions are equivalent to the following: is a category with given products such that the functors

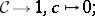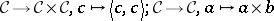have each a specified right-adjoint, written respectively as:

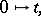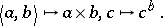Some examples of Cartesian-closed categories are:

E1) any Heyting algebra ;

E2) the category 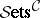for any small category with 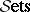the category of (small) sets — in particular 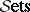itself;

E3) the category of sheaves over a topological space, and more generally a (Grothendieck) topos;

E4) any elementary topos ;

E5) the category of all (small) categories;

E6) the category 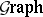of graphs and their homomorphisms;

E7) the category - of -CPOs.

These definitions can all be put into a purely equational form.

References

[a1]	M. Barr, C. Wells, "Category theory for computing science" , CRM (1990)
[a2]	J. Lambek, P.J. Scott, "Introduction to higher order categorical logic" , Cambridge Univ. Press (1986)
[a3]	S. MacLane, I. Moerdijk, "Sheaves in geometry and logic" , Springer (1992)
[a4]	S. MacLane, "Categories for the working mathematician" , Springer (1971)