Difference between revisions of "Core in the theory of games"
(Importing text file) |
m (links) |
||
| Line 1: | Line 1: | ||
The set of all non-dominated outcomes, that is, the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026490/c0264901.png" /> of outcomes such that a [[Domination|domination]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026490/c0264902.png" /> cannot hold for any outcomes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026490/c0264903.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026490/c0264904.png" /> and coalition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026490/c0264905.png" />. One defines in this respect: | The set of all non-dominated outcomes, that is, the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026490/c0264901.png" /> of outcomes such that a [[Domination|domination]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026490/c0264902.png" /> cannot hold for any outcomes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026490/c0264903.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026490/c0264904.png" /> and coalition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026490/c0264905.png" />. One defines in this respect: | ||
| − | 1) The core. The set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026490/c0264906.png" /> of | + | 1) The core. The set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026490/c0264906.png" /> of [[imputation]]s that are not dominated by any other imputation; the core coincides with the set of imputations satisfying <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026490/c0264907.png" /> for any coalition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026490/c0264908.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026490/c0264909.png" /> and a von Neumann–Morgenstern solution (see [[Solution in game theory]]) exists, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026490/c02649010.png" /> is contained in any von Neumann–Morgenstern solution. |
| − | 2) The kernel. The set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026490/c02649011.png" /> of individually rational configurations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026490/c02649012.png" /> (see [[ | + | 2) The kernel. The set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026490/c02649011.png" /> of individually rational configurations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026490/c02649012.png" /> (see [[Stability in game theory]]) such that the following inequality holds for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026490/c02649013.png" />: |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026490/c02649014.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026490/c02649014.png" /></td> </tr></table> | ||
| Line 16: | Line 16: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> N.N. Vorob'ev, "The present state of the theory of games" ''Russian Math. Surveys'' , '''25''' : 2 (1970) pp. 77–136 ''Uspekhi Mat. Nauk'' , '''25''' : 2 (1970) pp. 103–107</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[1]</TD> <TD valign="top"> N.N. Vorob'ev, "The present state of the theory of games" ''Russian Math. Surveys'' , '''25''' : 2 (1970) pp. 77–136 ''Uspekhi Mat. Nauk'' , '''25''' : 2 (1970) pp. 103–107</TD></TR> | ||
| + | </table> | ||
====Comments==== | ====Comments==== | ||
| − | The Russian word ( "yadro" ) is the same for all three notions defined above, but these notions may be distinguished by prefixing with the corresponding English letter ( "c | + | The Russian word ( "yadro" ) is the same for all three notions defined above, but these notions may be distinguished by prefixing with the corresponding English letter ( "c-yadro" for core, "k-yadro" for kernel and "n-yadro" for nucleolus). These three notions do not share many properties. |
See [[#References|[a1]]], [[#References|[a7]]] for core, [[#References|[a2]]] for kernel and [[#References|[a3]]] for nucleolus. [[#References|[a4]]], [[#References|[a5]]] are general references. [[#References|[a6]]] deals also with mathematical economics and the role of the concept of the core of a game in that setting. | See [[#References|[a1]]], [[#References|[a7]]] for core, [[#References|[a2]]] for kernel and [[#References|[a3]]] for nucleolus. [[#References|[a4]]], [[#References|[a5]]] are general references. [[#References|[a6]]] deals also with mathematical economics and the role of the concept of the core of a game in that setting. | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> O.N. Bondareva, "Certain applications of the methods of linear programming to the theory of cooperative games" ''Probl. Kibernet'' , '''10''' (1963) pp. 119–139 (In Russian)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Maschler, M. Davis, "The kernel of a cooperative game" ''Naval Res. Logist. Quart.'' , '''12''' (1965) pp. 223–259</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> D. Schmeidler, "The nucleolus of a characteristic function game" ''SIAM J. Appl. Math.'' , '''17''' (1969) pp. 1163–1170</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> G. Owen, "Game theory" , Acad. Press (1982)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> J. Szép, F. Forgó, "Introduction to the theory of games" , Reidel (1985) pp. 171; 199</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> J. Rosenmüller, "Cooperative games and markets" , North-Holland (1981)</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> L.S. Shapley, "On balanced sets and cores" ''Naval Res. Logist. Quart.'' , '''14''' (1967) pp. 453–460</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> O.N. Bondareva, "Certain applications of the methods of linear programming to the theory of cooperative games" ''Probl. Kibernet'' , '''10''' (1963) pp. 119–139 (In Russian)</TD></TR> | ||
| + | <TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Maschler, M. Davis, "The kernel of a cooperative game" ''Naval Res. Logist. Quart.'' , '''12''' (1965) pp. 223–259</TD></TR> | ||
| + | <TR><TD valign="top">[a3]</TD> <TD valign="top"> D. Schmeidler, "The nucleolus of a characteristic function game" ''SIAM J. Appl. Math.'' , '''17''' (1969) pp. 1163–1170</TD></TR> | ||
| + | <TR><TD valign="top">[a4]</TD> <TD valign="top"> G. Owen, "Game theory" , Acad. Press (1982)</TD></TR> | ||
| + | <TR><TD valign="top">[a5]</TD> <TD valign="top"> J. Szép, F. Forgó, "Introduction to the theory of games" , Reidel (1985) pp. 171; 199</TD></TR> | ||
| + | <TR><TD valign="top">[a6]</TD> <TD valign="top"> J. Rosenmüller, "Cooperative games and markets" , North-Holland (1981)</TD></TR> | ||
| + | <TR><TD valign="top">[a7]</TD> <TD valign="top"> L.S. Shapley, "On balanced sets and cores" ''Naval Res. Logist. Quart.'' , '''14''' (1967) pp. 453–460</TD></TR> | ||
| + | </table> | ||
Revision as of 18:20, 9 January 2016
The set of all non-dominated outcomes, that is, the set 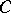 of outcomes such that a domination
of outcomes such that a domination 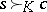 cannot hold for any outcomes
cannot hold for any outcomes 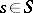 ,
,  and coalition
and coalition 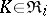 . One defines in this respect:
. One defines in this respect:
1) The core. The set 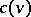 of imputations that are not dominated by any other imputation; the core coincides with the set of imputations satisfying
of imputations that are not dominated by any other imputation; the core coincides with the set of imputations satisfying 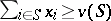 for any coalition
for any coalition 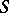 . If
. If 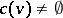 and a von Neumann–Morgenstern solution (see Solution in game theory) exists, then
and a von Neumann–Morgenstern solution (see Solution in game theory) exists, then  is contained in any von Neumann–Morgenstern solution.
is contained in any von Neumann–Morgenstern solution.
2) The kernel. The set 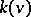 of individually rational configurations
of individually rational configurations 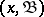 (see Stability in game theory) such that the following inequality holds for any
(see Stability in game theory) such that the following inequality holds for any 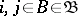 :
:
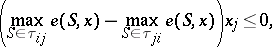 |
where 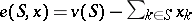 and
and 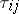 is the set of coalitions containing the player
is the set of coalitions containing the player 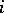 and not containing the player
and not containing the player 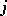 . The kernel
. The kernel 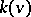 is contained in an
is contained in an 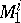 -bargaining set.
-bargaining set.
3) The nucleolus. The minimal imputation 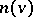 relative to the quasi-order
relative to the quasi-order 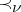 defined on the set of imputations by:
defined on the set of imputations by: 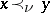 if and only if the vector
if and only if the vector 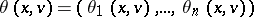 , where
, where
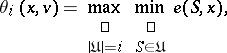 |
lexicographically precedes 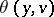 . The nucleolus
. The nucleolus 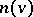 exists and is unique for any game with a non-empty set of imputations. In a cooperative game the nucleolus is contained in the kernel.
exists and is unique for any game with a non-empty set of imputations. In a cooperative game the nucleolus is contained in the kernel.
References
| [1] | N.N. Vorob'ev, "The present state of the theory of games" Russian Math. Surveys , 25 : 2 (1970) pp. 77–136 Uspekhi Mat. Nauk , 25 : 2 (1970) pp. 103–107 |
Comments
The Russian word ( "yadro" ) is the same for all three notions defined above, but these notions may be distinguished by prefixing with the corresponding English letter ( "c-yadro" for core, "k-yadro" for kernel and "n-yadro" for nucleolus). These three notions do not share many properties.
See [a1], [a7] for core, [a2] for kernel and [a3] for nucleolus. [a4], [a5] are general references. [a6] deals also with mathematical economics and the role of the concept of the core of a game in that setting.
References
| [a1] | O.N. Bondareva, "Certain applications of the methods of linear programming to the theory of cooperative games" Probl. Kibernet , 10 (1963) pp. 119–139 (In Russian) |
| [a2] | M. Maschler, M. Davis, "The kernel of a cooperative game" Naval Res. Logist. Quart. , 12 (1965) pp. 223–259 |
| [a3] | D. Schmeidler, "The nucleolus of a characteristic function game" SIAM J. Appl. Math. , 17 (1969) pp. 1163–1170 |
| [a4] | G. Owen, "Game theory" , Acad. Press (1982) |
| [a5] | J. Szép, F. Forgó, "Introduction to the theory of games" , Reidel (1985) pp. 171; 199 |
| [a6] | J. Rosenmüller, "Cooperative games and markets" , North-Holland (1981) |
| [a7] | L.S. Shapley, "On balanced sets and cores" Naval Res. Logist. Quart. , 14 (1967) pp. 453–460 |
Core in the theory of games. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Core_in_the_theory_of_games&oldid=14089