|
|
| Line 1: |
Line 1: |
| − | ''with respect to two given lines <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012660/a0126601.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012660/a0126602.png" />'' | + | {{TEX|done}} |
| | + | ''with respect to two given lines $m_1$ and $m_2$'' |
| | | | |
| − | Two straight lines <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012660/a0126603.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012660/a0126604.png" /> which intersect <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012660/a0126605.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012660/a0126606.png" /> so that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012660/a0126607.png" /> (cf. Fig.). | + | Two straight lines $l_1$ and $l_2$ which intersect $m_1$ and $m_2$ so that $\angle1=\angle2$ (cf. Fig.). |
| | | | |
| | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/a012660a.gif" /> | | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/a012660a.gif" /> |
| Line 7: |
Line 8: |
| | Figure: a012660a | | Figure: a012660a |
| | | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012660/a0126608.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012660/a0126609.png" /> are anti-parallel with respect to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012660/a01266010.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012660/a01266011.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012660/a01266012.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012660/a01266013.png" /> are also anti-parallel with respect to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012660/a01266014.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012660/a01266015.png" />. In any quadrilateral inscribed in a circle, any two opposite sides are anti-parallel with respect to the other two sides. If the lines <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012660/a01266016.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012660/a01266017.png" /> intersect at a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012660/a01266018.png" />, one also says that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012660/a01266019.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012660/a01266020.png" /> are anti-parallel with respect to the angle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012660/a01266021.png" />. If the lines <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012660/a01266022.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012660/a01266023.png" /> coincide, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012660/a01266024.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012660/a01266025.png" /> are said to be anti-parallel with respect to a straight line. | + | If $l_1$ and $l_2$ are anti-parallel with respect to $m_1$ and $m_2$, then $m_1$ and $m_2$ are also anti-parallel with respect to $l_1$ and $l_2$. In any quadrilateral inscribed in a circle, any two opposite sides are anti-parallel with respect to the other two sides. If the lines $m_1$ and $m_2$ intersect at a point $O$, one also says that $l_1$ and $l_2$ are anti-parallel with respect to the angle $m_1Om_2$. If the lines $m_1$ and $m_2$ coincide, $l_1$ and $l_2$ are said to be anti-parallel with respect to a straight line. |
Revision as of 18:02, 11 April 2014
with respect to two given lines $m_1$ and $m_2$
Two straight lines $l_1$ and $l_2$ which intersect $m_1$ and $m_2$ so that $\angle1=\angle2$ (cf. Fig.).
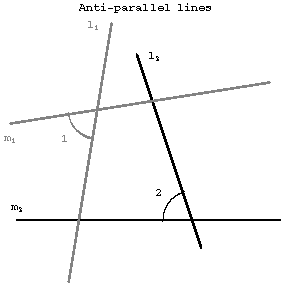
Figure: a012660a
If $l_1$ and $l_2$ are anti-parallel with respect to $m_1$ and $m_2$, then $m_1$ and $m_2$ are also anti-parallel with respect to $l_1$ and $l_2$. In any quadrilateral inscribed in a circle, any two opposite sides are anti-parallel with respect to the other two sides. If the lines $m_1$ and $m_2$ intersect at a point $O$, one also says that $l_1$ and $l_2$ are anti-parallel with respect to the angle $m_1Om_2$. If the lines $m_1$ and $m_2$ coincide, $l_1$ and $l_2$ are said to be anti-parallel with respect to a straight line.
How to Cite This Entry:
Anti-parallel straight lines. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Anti-parallel_straight_lines&oldid=13704
This article was adapted from an original article by A.B. Ivanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article