Difference between revisions of "Gauss kernel"
From Encyclopedia of Mathematics
(Importing text file) |
(→References: Feller: internal link) |
||
| Line 18: | Line 18: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P. Butzer, R. Nessel, "Fourier analysis and approximation", '''I''', Birkhäuser (1971)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R. Courant, D. Hilbert, "Methods of mathematical physics", '''II''', Wiley (1962)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> W. Feller, [[Feller, "An introduction to probability theory and its applications"|"An introduction to probability theory and its applications"]], '''2''', Springer (1976) (Edition: Second)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> E.C. Titchmarsh, "Introduction to the theory of Fourier integrals", Clarendon Press (1937)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> K. Weierstrass, "Ueber die analytische Darstellbarkeit sogenannter willkurlichen Functionen reeler Argumente" ''Berliner Sitzungsberichte'' (1985) pp. 633–639; 789–805</TD></TR></table> |
Revision as of 09:09, 4 May 2012
The 
-dimensional Gauss (or Weierstrass) kernel
 |
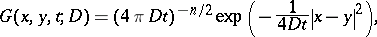with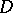 
a positive constant, 
, 
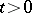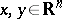, is the fundamental solution of the 
-dimensional heat equation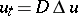 
. Moreover, this kernel is an approximate identity in that the Gauss–Weierstrass singular integral at the function 
,
 |
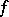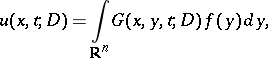satisfies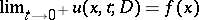 
almost everywhere, for example, whenever 
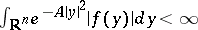for some 
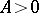; see [a4]. Thus 
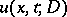is a solution of the heat equation for 
, 
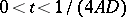having the initial "temperature"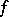 
.
In the theory of Markov processes (cf. Markov process) the Gauss kernel gives the transition probability density of the Wiener–Lévy process (or of Brownian motion). The semi-group property of the Gauss kernel
 |
 |
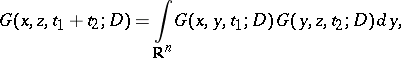is essential here.
References
| [a1] | P. Butzer, R. Nessel, "Fourier analysis and approximation", I, Birkhäuser (1971) |
| [a2] | R. Courant, D. Hilbert, "Methods of mathematical physics", II, Wiley (1962) |
| [a3] | W. Feller, "An introduction to probability theory and its applications", 2, Springer (1976) (Edition: Second) |
| [a4] | E.C. Titchmarsh, "Introduction to the theory of Fourier integrals", Clarendon Press (1937) |
| [a5] | K. Weierstrass, "Ueber die analytische Darstellbarkeit sogenannter willkurlichen Functionen reeler Argumente" Berliner Sitzungsberichte (1985) pp. 633–639; 789–805 |
How to Cite This Entry:
Gauss kernel. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gauss_kernel&oldid=13441
Gauss kernel. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gauss_kernel&oldid=13441
This article was adapted from an original article by R. Kerman (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article