Difference between revisions of "Gradient method"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 13: | Line 13: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J.E. Dennis, R.B. Schnabel, "Numerical methods for unconstrained optimization and nonlinear equations" , Prentice-Hall (1983)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R. Fletcher, "Practical methods of optimization" , Wiley (1980)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> D.G. Luenberger, "Linear and nonlinear programming" , Addison-Wesley (1984)</TD></TR></table> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J.E. Dennis, R.B. Schnabel, "Numerical methods for unconstrained optimization and nonlinear equations" , Prentice-Hall (1983) {{MR|0702023}} {{ZBL|0579.65058}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R. Fletcher, "Practical methods of optimization" , Wiley (1980) {{MR|0585160}} {{MR|0633058}} {{ZBL|0439.93001}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> D.G. Luenberger, "Linear and nonlinear programming" , Addison-Wesley (1984) {{MR|2423726}} {{MR|2012832}} {{ZBL|0571.90051}} </TD></TR></table> |
Revision as of 11:59, 27 September 2012
A method for the minimization of a function of several variables. It is based on the fact that each successive approximation of the function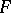 
is obtained from the preceding one by a shift in the direction of the gradient of the function:
 |
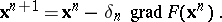The parameter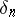 
can be obtained, e.g., from the condition of the magnitude
 |
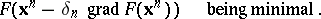See also Descent, method of; Steepest descent, method of.
Comments
References
| [a1] | J.E. Dennis, R.B. Schnabel, "Numerical methods for unconstrained optimization and nonlinear equations" , Prentice-Hall (1983) MR0702023 Zbl 0579.65058 |
| [a2] | R. Fletcher, "Practical methods of optimization" , Wiley (1980) MR0585160 MR0633058 Zbl 0439.93001 |
| [a3] | D.G. Luenberger, "Linear and nonlinear programming" , Addison-Wesley (1984) MR2423726 MR2012832 Zbl 0571.90051 |
How to Cite This Entry:
Gradient method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gradient_method&oldid=13020
Gradient method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gradient_method&oldid=13020