Difference between revisions of "Kauffman bracket polynomial"
(Importing text file) |
m (AUTOMATIC EDIT (latexlist): Replaced 49 formulas out of 51 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 51 formulas, 49 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|partial}} | ||
An invariant of unoriented framed links. | An invariant of unoriented framed links. | ||
| − | It is a Laurent polynomial of one variable associated to ambient isotopy classes of unoriented framed links in | + | It is a Laurent polynomial of one variable associated to ambient isotopy classes of unoriented framed links in $\mathbf{R} ^ { 3 }$ (or $S ^ { 3 }$), constructed by L.H. Kauffman in the summer of 1985 and denoted by $\langle L \rangle$. It is defined recursively as follows: For a trivial link of $n$ components, with zero framing, $T _ { n }$, one puts |
| − | + | \begin{equation*} \langle T _ { n } \rangle = ( - A ^ { 2 } - A ^ { - 2 } ) ^ { n - 1 }. \end{equation*} | |
For the Kauffman bracket skein triple (cf. Fig.a1) one has the Kauffman bracket skein relation: | For the Kauffman bracket skein triple (cf. Fig.a1) one has the Kauffman bracket skein relation: | ||
| − | + | \begin{equation*} \langle L _ { + } \rangle = A \langle L _ { 0 } \rangle + A ^ { - 1 } \langle L _ { \infty } \rangle . \end{equation*} | |
| − | <img | + | <img src="https://www.encyclopediaofmath.org/legacyimages/common_img/k130010a.gif" style="border:1px solid;"/> |
Figure: k130010a | Figure: k130010a | ||
| − | If | + | If $L ^ { ( 1 ) }$ is obtained from $L$ by a positive full twist on its framing, then $\langle L ^ { ( 1 ) } \rangle = - A ^ { 3 } \langle L \rangle$. The Kauffman bracket polynomial is also considered as an invariant of regular isotopy (Reidemeister moves: $R _ { 2 }$, $R _ { 3 }$, cf. [[Reidemeister theorem|Reidemeister theorem]]) of diagrams on the plane. $\langle D \rangle$ is changed by the first Reidemeister move by $- A ^ { \pm 3 }$. |
The Kauffman bracket polynomial is related to a substitution of the dichromatic polynomial of signed graphs. This connection also relates the Kauffman bracket polynomial to the Potts model in statistical mechanics. State sum expansions of the dichromatic polynomial have their analogue for the Kauffman bracket polynomial. For example: | The Kauffman bracket polynomial is related to a substitution of the dichromatic polynomial of signed graphs. This connection also relates the Kauffman bracket polynomial to the Potts model in statistical mechanics. State sum expansions of the dichromatic polynomial have their analogue for the Kauffman bracket polynomial. For example: | ||
| − | + | \begin{equation*} \langle D \rangle = \sum _ { s } A ^ { T ( s ) } ( - A ^ { 2 } - A ^ { - 2 } ) ^ { | s D | - 1 }, \end{equation*} | |
| − | where the sum is taken over all states of the link diagram | + | where the sum is taken over all states of the link diagram $D$ and where a state codes the type of the smoothing performed at each crossing ($L_0$ or $L _ { \infty }$ type). $T ( s )$ denotes the number of smoothings of type $L_0$ minus the number of smoothings of type $L _ { \infty }$. $| s D |$ denotes the number of components of the diagram after all $s$-smoothings on $D$ are performed. |
| − | The Kauffman bracket polynomial has a straightforward generalization to the solid torus (projected onto the annulus) and to the genus-two handlebody (projected onto the disc with | + | The Kauffman bracket polynomial has a straightforward generalization to the solid torus (projected onto the annulus) and to the genus-two handlebody (projected onto the disc with $2$ holes). In the first case it has values in $\mathbf{Z} [ A ^ { \pm 1 } , \alpha ]$ and in the second case it has values in $\mathbf{Z} [ A ^ { \pm 1 } , a , b , c ]$, see Fig.a2. |
| − | <img | + | <img src="https://www.encyclopediaofmath.org/legacyimages/common_img/k130010b.gif" style="border:1px solid;"/> |
Figure: k130010b | Figure: k130010b | ||
| − | For links in a solid torus the bracket polynomial can be used to estimate the wrapping number of the link. The wrapping conjecture says that | + | For links in a solid torus the bracket polynomial can be used to estimate the wrapping number of the link. The wrapping conjecture says that $\operatorname{wrap}( D )$ for a link diagram $D$ in the annulus is equal to the $\alpha$-degree of $\langle D \rangle$ [[#References|[a1]]]. The Kauffman bracket skein module (cf. [[Skein module|Skein module]]) is a generalization of the Kauffman bracket polynomial to any $3$-dimensional manifold. |
| − | The Kauffman bracket polynomial is a variant of the Jones polynomial. If one chooses an orientation | + | The Kauffman bracket polynomial is a variant of the Jones polynomial. If one chooses an orientation $ \overset{\rightharpoonup}{ D }$ on an unoriented link diagram $D$, then one defines an oriented link invariant $f ( \overset{\rightharpoonup}{ D } ( A ) ) = ( - A ^ { 3 } ) ^ { - \operatorname { Tait } ( \overset{\rightharpoonup}{ D } ) } ( D )$, where $\operatorname{Tait}( \vec { D } )$ is the Tait number (or writhe number) of $ \overset{\rightharpoonup}{ D }$, defined to be the sum of signs over all crossings of $ \overset{\rightharpoonup}{ D }$. Then the Jones polynomial $V _ { L } ( t ) = f _ { L } ( A )$ for $t = A ^ { - 4 }$. Furthermore, the Kauffman bracket polynomial satisfies: |
| − | + | \begin{equation*} A \langle D _ { + } \rangle - A ^ { - 1 } \langle D _ { - } \rangle = ( A ^ { 2 } - A ^ { - 2 } ) \langle D _ { 0 } \rangle \end{equation*} | |
and | and | ||
| − | + | \begin{equation*} \langle D _ { + } \rangle + \langle D _ { - } \rangle = ( A + A ^ { - 1 } ) ( \langle D _ { 0 } \rangle + \langle D _ { \infty } \rangle ), \end{equation*} | |
and it is a specialization of both the [[Jones–Conway polynomial|Jones–Conway polynomial]] and the [[Kauffman polynomial|Kauffman polynomial]]. | and it is a specialization of both the [[Jones–Conway polynomial|Jones–Conway polynomial]] and the [[Kauffman polynomial|Kauffman polynomial]]. | ||
| − | The Kauffman bracket polynomial was essential in the proof of the Tait conjectures on alternating links. In particular, for a connected alternating diagram without a nugatory crossing | + | The Kauffman bracket polynomial was essential in the proof of the Tait conjectures on alternating links. In particular, for a connected alternating diagram without a nugatory crossing $\operatorname { span } \langle D \rangle = 4 c ( D )$, where $c ( D )$ is the number of crossing points of $D$. If the diagram is prime and non-alternating, then $\operatorname { span } \langle D \rangle < 4 c ( D )$. |
| − | The Kauffman bracket polynomial has several other applications, for example in the analysis of periodic links. The Reshetikhin–Turaev invariants of | + | The Kauffman bracket polynomial has several other applications, for example in the analysis of periodic links. The Reshetikhin–Turaev invariants of $3$-manifolds can be constructed using the Kauffman bracket polynomial (via Kirby moves, cf. also [[Kirby calculus|Kirby calculus]]) [[#References|[a5]]]. |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> J. Hoste, J.H. Przytycki, "An invariant of dichromatic links" ''Proc. Amer. Math. Soc.'' , '''105''' : 4 (1989) pp. 1003–1007</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> V.F.R. Jones, "Hecke algebra representations of braid groups and link polynomials" ''Ann. of Math.'' , '''126''' : 2 (1987) pp. 335–388</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> L.H. Kauffman, "State models and the Jones polynomial" ''Topology'' , '''26''' (1987) pp. 395–407</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> L.H. Kauffman, "An invariant of regular isotopy" ''Trans. Amer. Math. Soc.'' , '''318''' : 2 (1990) pp. 417–471</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> W.B.R. Lickorish, "An introduction to knot theory" , Springer (1997)</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> W.M. Menasco, M.B. Thistlethwaite, "The classification of alternating links" ''Ann. of Math.'' , '''138''' (1993) pp. 113–171</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> K. Murasugi, "Jones polynomial and classical conjectures in knot theory" ''Topology'' , '''26''' : 2 (1987) pp. 187–194</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> P. Traczyk, "$10_{101}$ has no period $7$: a criterion for periodic links" ''Proc. Amer. Math. Soc.'' , '''180''' (1990) pp. 845–846</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> M.B. Thistlethwaite, "Kauffman polynomial and alternating links" ''Topology'' , '''27''' (1988) pp. 311–318</td></tr></table> |
Revision as of 16:55, 1 July 2020
An invariant of unoriented framed links.
It is a Laurent polynomial of one variable associated to ambient isotopy classes of unoriented framed links in $\mathbf{R} ^ { 3 }$ (or $S ^ { 3 }$), constructed by L.H. Kauffman in the summer of 1985 and denoted by $\langle L \rangle$. It is defined recursively as follows: For a trivial link of $n$ components, with zero framing, $T _ { n }$, one puts
\begin{equation*} \langle T _ { n } \rangle = ( - A ^ { 2 } - A ^ { - 2 } ) ^ { n - 1 }. \end{equation*}
For the Kauffman bracket skein triple (cf. Fig.a1) one has the Kauffman bracket skein relation:
\begin{equation*} \langle L _ { + } \rangle = A \langle L _ { 0 } \rangle + A ^ { - 1 } \langle L _ { \infty } \rangle . \end{equation*}
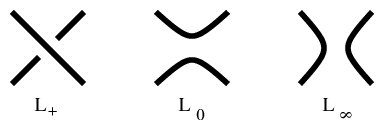
Figure: k130010a
If $L ^ { ( 1 ) }$ is obtained from $L$ by a positive full twist on its framing, then $\langle L ^ { ( 1 ) } \rangle = - A ^ { 3 } \langle L \rangle$. The Kauffman bracket polynomial is also considered as an invariant of regular isotopy (Reidemeister moves: $R _ { 2 }$, $R _ { 3 }$, cf. Reidemeister theorem) of diagrams on the plane. $\langle D \rangle$ is changed by the first Reidemeister move by $- A ^ { \pm 3 }$.
The Kauffman bracket polynomial is related to a substitution of the dichromatic polynomial of signed graphs. This connection also relates the Kauffman bracket polynomial to the Potts model in statistical mechanics. State sum expansions of the dichromatic polynomial have their analogue for the Kauffman bracket polynomial. For example:
\begin{equation*} \langle D \rangle = \sum _ { s } A ^ { T ( s ) } ( - A ^ { 2 } - A ^ { - 2 } ) ^ { | s D | - 1 }, \end{equation*}
where the sum is taken over all states of the link diagram $D$ and where a state codes the type of the smoothing performed at each crossing ($L_0$ or $L _ { \infty }$ type). $T ( s )$ denotes the number of smoothings of type $L_0$ minus the number of smoothings of type $L _ { \infty }$. $| s D |$ denotes the number of components of the diagram after all $s$-smoothings on $D$ are performed.
The Kauffman bracket polynomial has a straightforward generalization to the solid torus (projected onto the annulus) and to the genus-two handlebody (projected onto the disc with $2$ holes). In the first case it has values in $\mathbf{Z} [ A ^ { \pm 1 } , \alpha ]$ and in the second case it has values in $\mathbf{Z} [ A ^ { \pm 1 } , a , b , c ]$, see Fig.a2.
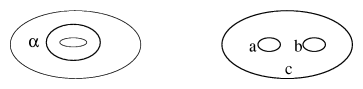
Figure: k130010b
For links in a solid torus the bracket polynomial can be used to estimate the wrapping number of the link. The wrapping conjecture says that $\operatorname{wrap}( D )$ for a link diagram $D$ in the annulus is equal to the $\alpha$-degree of $\langle D \rangle$ [a1]. The Kauffman bracket skein module (cf. Skein module) is a generalization of the Kauffman bracket polynomial to any $3$-dimensional manifold.
The Kauffman bracket polynomial is a variant of the Jones polynomial. If one chooses an orientation $ \overset{\rightharpoonup}{ D }$ on an unoriented link diagram $D$, then one defines an oriented link invariant $f ( \overset{\rightharpoonup}{ D } ( A ) ) = ( - A ^ { 3 } ) ^ { - \operatorname { Tait } ( \overset{\rightharpoonup}{ D } ) } ( D )$, where $\operatorname{Tait}( \vec { D } )$ is the Tait number (or writhe number) of $ \overset{\rightharpoonup}{ D }$, defined to be the sum of signs over all crossings of $ \overset{\rightharpoonup}{ D }$. Then the Jones polynomial $V _ { L } ( t ) = f _ { L } ( A )$ for $t = A ^ { - 4 }$. Furthermore, the Kauffman bracket polynomial satisfies:
\begin{equation*} A \langle D _ { + } \rangle - A ^ { - 1 } \langle D _ { - } \rangle = ( A ^ { 2 } - A ^ { - 2 } ) \langle D _ { 0 } \rangle \end{equation*}
and
\begin{equation*} \langle D _ { + } \rangle + \langle D _ { - } \rangle = ( A + A ^ { - 1 } ) ( \langle D _ { 0 } \rangle + \langle D _ { \infty } \rangle ), \end{equation*}
and it is a specialization of both the Jones–Conway polynomial and the Kauffman polynomial.
The Kauffman bracket polynomial was essential in the proof of the Tait conjectures on alternating links. In particular, for a connected alternating diagram without a nugatory crossing $\operatorname { span } \langle D \rangle = 4 c ( D )$, where $c ( D )$ is the number of crossing points of $D$. If the diagram is prime and non-alternating, then $\operatorname { span } \langle D \rangle < 4 c ( D )$.
The Kauffman bracket polynomial has several other applications, for example in the analysis of periodic links. The Reshetikhin–Turaev invariants of $3$-manifolds can be constructed using the Kauffman bracket polynomial (via Kirby moves, cf. also Kirby calculus) [a5].
References
| [a1] | J. Hoste, J.H. Przytycki, "An invariant of dichromatic links" Proc. Amer. Math. Soc. , 105 : 4 (1989) pp. 1003–1007 |
| [a2] | V.F.R. Jones, "Hecke algebra representations of braid groups and link polynomials" Ann. of Math. , 126 : 2 (1987) pp. 335–388 |
| [a3] | L.H. Kauffman, "State models and the Jones polynomial" Topology , 26 (1987) pp. 395–407 |
| [a4] | L.H. Kauffman, "An invariant of regular isotopy" Trans. Amer. Math. Soc. , 318 : 2 (1990) pp. 417–471 |
| [a5] | W.B.R. Lickorish, "An introduction to knot theory" , Springer (1997) |
| [a6] | W.M. Menasco, M.B. Thistlethwaite, "The classification of alternating links" Ann. of Math. , 138 (1993) pp. 113–171 |
| [a7] | K. Murasugi, "Jones polynomial and classical conjectures in knot theory" Topology , 26 : 2 (1987) pp. 187–194 |
| [a8] | P. Traczyk, "$10_{101}$ has no period $7$: a criterion for periodic links" Proc. Amer. Math. Soc. , 180 (1990) pp. 845–846 |
| [a9] | M.B. Thistlethwaite, "Kauffman polynomial and alternating links" Topology , 27 (1988) pp. 311–318 |
Kauffman bracket polynomial. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kauffman_bracket_polynomial&oldid=12747