Conjugate elements

in a group

Elements and of for which

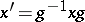for some in . One also says that is the result of conjugating by 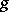. The power notation 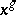is frequently used for the conjugate of under .

Let 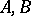be two subsets of a group , then 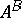denotes the set

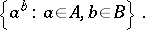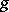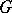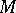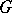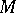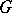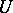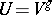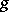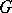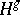For some fixed in and some subset of the set is said to be conjugate to the set in . In particular, two subgroups and are called conjugate subgroups if for some in . If a subgroup coincides with for every 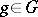(that is, consists of all conjugates of all its elements), then is called a normal subgroup of 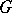(or an invariant subgroup, or, rarely, a self-conjugate subgroup).

Comments

The map $x \mapsto g^{-1} x g$ for given $g$ is conjugation by $g$: it is an inter automorphism of $G$.

References

[a1]	B. Huppert, "Endliche Gruppen" , 1 , Springer (1967)
[a2]	D. Gorenstein, "Finite groups" , Chelsea, reprint (1980)