Dirichlet Laplacian

Dirichlet–Laplace operator

In a broad sense, a restriction of the Laplace operator to the space of functions satisfying (in some sense) homogeneous Dirichlet boundary conditions. For an open set in , the Dirichlet Laplacian is usually defined via the Friedrichs extension procedure. Namely, first consider the (negative) Laplace operator defined on the subspace of all infinitely smooth functions with compact support in . This is a symmetric operator, and the associated quadratic form (with the same domain ) is given by the Dirichlet integral

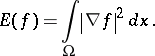(a1)

Then the form is closeable with respect to the norm

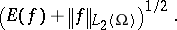The domain of its closure 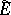is the Sobolev space . Then 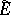(given again by the right-hand side of (a1)) is the quadratic form of a non-negative self-adjoint operator (denoted by 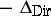); moreover,

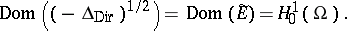The operator 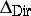(sometimes taken with the minus sign) is called the Dirichlet Laplacian (in the weak sense).

If is bounded domain with boundary of class 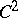, then

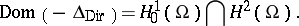The Dirichlet Laplacian for a compact Riemannian manifold with boundary is defined similarly.

For a bounded open set in , is a positive unbounded linear operator in with a discrete spectrum (cf. also Spectrum of an operator). Its eigenvalues (written in increasing order with account of multiplicity) can be found using the Rayleigh–Ritz variational formula (or max-min formula)

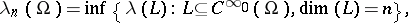where

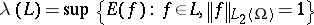for a finite-dimensional linear subspace 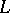of . It follows from the Rayleigh–Ritz formula that the eigenvalues 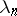are monotonically decreasing functions of . See also [a3] for a survey of the asymptotic behaviour of the eigenvalues of the Dirichlet Laplacian and operators corresponding to other boundary value problems for elliptic differential operators.

References

[a1]	E.B. Davies, "Spectral theory and differential operators" , Cambridge Univ. Press (1995) MR1349825 Zbl 0893.47004
[a2]	D.E. Edmunds, W.D. Ewans, "Spectral theory and differential operators" , Clarendon Press (1987) MR0929030 Zbl 0628.47017
[a3]	Yu. Safarov, D. Vassiliev, "The asymptotic distribution of eigenvalues of partial differential operators" , Transl. Math. Monogr. , 55 , Amer. Math. Soc. (1997) MR1414899 Zbl 0898.35003 Zbl 0870.35003