Lie algebra, free

over a ring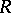

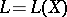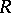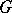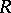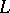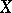A Lie algebra over in which one can distinguish a free generating set , a mapping from which into an arbitrary algebra over can be be extended to a homomorphism from into . The cardinality of completely determines 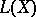and is called its rank. A free Lie algebra is a free -module (for bases of it see Basic commutator). A subalgebra of a free Lie algebra over a field is itself a free Lie algebra (Shirshov's theorem, [1]). If 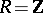, then this is true only under the condition that is a free Abelian group [2]. The finitely-generated subalgebras of a free Lie algebra over a field form a sublattice of the lattice of all subalgebras [3]. W. Magnus [4] established canonical connections between free Lie algebras and both free groups and free associative algebras.

References

[1]	A.I. Shirshov, "Subalgebras of free Lie algebras" Mat. Sb. , 33 : 2 (1953) pp. 441–452 (In Russian)
[2]	E. Witt, "Die Unterringe der freien Lieschen Ringe" Math. Z. , 64 (1956) pp. 195–216
[3]	G.P. Kukin, "Intersection of subalgebras of a free Lie algebra" Algebra and Logic , 16 (1977) pp. 387–394 Algebra i Logika , 16 (1977) pp. 577–587
[4]	W. Magnus, "Ueber Beziehungen zwischen höheren Kommutatoren" J. Reine Angew. Math. , 177 (1937) pp. 105–115
[5]	Yu.A. Bakhturin, "Identical relations in Lie algebras" , VNU , Utrecht (1987) (Translated from Russian)

Comments

To construct 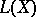one can start from the free associative algebra 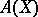generated by 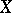, which is made into a Lie algebra 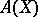by taking as Lie product . Then 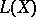is the Lie subalgebra of generated by 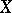, and 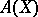is the universal enveloping algebra of .

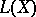In case 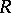is a field of characteristic 0, more precise results on which elements of belong to are given by the Specht–Wever theorem and the Friedrichs theorem, respectively. The first one says that a homogeneous element of degree 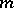belongs to 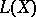if and only if , where is the linear mapping defined by

for 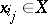. Friedrichs' theorem says for the case of finite 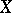that 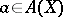belongs to 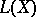if and only if 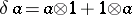, where 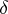is the homomorphism 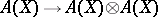defined by 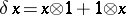for .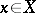

Free Lie algebras are the best context for the formulation of the Campbell–Baker–Hausdorff formula in its most general form.

References

[a1]	N. Jacobson, "Lie algebras" , Interscience (1962) ((also: Dover, reprint, 1979))
[a2]	N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French)