Difference between revisions of "Complete algebraic variety"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 4: | Line 4: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> R. Hartshorne, "Algebraic geometry" , Springer (1977) {{MR|0463157}} {{ZBL|0367.14001}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) {{MR|0447223}} {{ZBL|0362.14001}} </TD></TR></table> |
Revision as of 21:51, 30 March 2012
A generalization of the concept of a compact complex algebraic variety. A separated variety 
is called complete if for any variety 
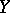the projection 
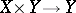is a closed morphism, i.e. it maps closed subsets of 
(in the Zariski topology) into closed subsets of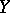 
. There is what is called the valuative completeness criterion: For any discrete valuation ring 
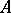with field of fractions 
and any morphism 
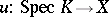there should be a unique morphism 
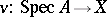that extends 
. This condition is an analogue of the requirement that any sequence in 
has a limit point.
Any projective variety is complete, but not vice versa. For any complete algebraic variety 
there exists a projective variety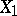 
and a projective birational morphism 
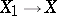(Chow's lemma). For any algebraic variety 
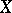there exists an open imbedding into a complete variety 
(Nagata's theorem). A generalization of the concept of a complete algebraic variety to the relative case is that of a proper morphism of schemes.
References
| [1] | R. Hartshorne, "Algebraic geometry" , Springer (1977) MR0463157 Zbl 0367.14001 |
| [2] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) MR0447223 Zbl 0362.14001 |
Complete algebraic variety. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complete_algebraic_variety&oldid=11651