Difference between revisions of "Standard construction"
Ulf Rehmann (talk | contribs) m (Undo revision 48800 by Ulf Rehmann (talk)) Tag: Undo |
m |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
A concept in category theory. Other names are [[Triple|triple]], monad and functor-algebra. | A concept in category theory. Other names are [[Triple|triple]], monad and functor-algebra. | ||
| − | Let | + | Let $\mathfrak{S}$ be a [[category]]. A standard construction is a functor $T : \mathfrak{S} \to \mathfrak{S}$ equipped with natural transformations $\eta : \operatorname{Id} \to T$ and $\mu : T^2 \to T$ such that the following diagrams commute: |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087140/s0871405.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087140/s0871405.png" /></td> </tr></table> | ||
The basic use of standard constructions in topology is in the construction of various classifying spaces and their algebraic analogues, the so-called bar-constructions. | The basic use of standard constructions in topology is in the construction of various classifying spaces and their algebraic analogues, the so-called bar-constructions. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | The term "standard construction" was introduced by R. Godement [[#References|[a1]]] for want of a better name for this concept. It is now entirely obsolete, having been generally superseded by "monad" (although a minority of authors still use the term "triple" ). Monads have many other uses besides the one mentioned above, for example in the categorical approach to [[ | + | The term "standard construction" was introduced by R. Godement [[#References|[a1]]] for want of a better name for this concept. It is now entirely obsolete, having been generally superseded by "monad" (although a minority of authors still use the term "triple" ). Monads have many other uses besides the one mentioned above, for example in the categorical approach to [[universal algebra]] (see [[#References|[a2]]], [[#References|[a3]]]). |
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Godement, "Théorie des faisceaux" , Hermann (1958)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> E.G. Manes, "Algebraic theories" , Springer (1976)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> M. Barr, C. Wells, "Toposes, triples and theories" , Springer (1985)</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[1]</TD> <TD valign="top"> J.M. Boardman, R.M. Vogt, "Homotopy invariant algebraic structures on topological spaces" , Springer (1973)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.F. Adams, "Infinite loop spaces" , Princeton Univ. Press (1978)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J.P. May, "The geometry of iterated loop spaces" , ''Lect. notes in math.'' , '''271''' , Springer (1972)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> S. MacLane, "Categories for the working mathematician" , Springer (1971)</TD></TR> | ||
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Godement, "Théorie des faisceaux" , Hermann (1958)</TD></TR> | ||
| + | <TR><TD valign="top">[a2]</TD> <TD valign="top"> E.G. Manes, "Algebraic theories" , Springer (1976)</TD></TR> | ||
| + | <TR><TD valign="top">[a3]</TD> <TD valign="top"> M. Barr, C. Wells, "Toposes, triples and theories" , Springer (1985)</TD></TR></table> | ||
Latest revision as of 09:03, 10 April 2023
A concept in category theory. Other names are triple, monad and functor-algebra.
Let $\mathfrak{S}$ be a category. A standard construction is a functor $T : \mathfrak{S} \to \mathfrak{S}$ equipped with natural transformations $\eta : \operatorname{Id} \to T$ and $\mu : T^2 \to T$ such that the following diagrams commute:
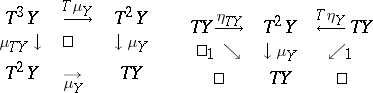 |
The basic use of standard constructions in topology is in the construction of various classifying spaces and their algebraic analogues, the so-called bar-constructions.
Comments
The term "standard construction" was introduced by R. Godement [a1] for want of a better name for this concept. It is now entirely obsolete, having been generally superseded by "monad" (although a minority of authors still use the term "triple" ). Monads have many other uses besides the one mentioned above, for example in the categorical approach to universal algebra (see [a2], [a3]).
References
| [1] | J.M. Boardman, R.M. Vogt, "Homotopy invariant algebraic structures on topological spaces" , Springer (1973) |
| [2] | J.F. Adams, "Infinite loop spaces" , Princeton Univ. Press (1978) |
| [3] | J.P. May, "The geometry of iterated loop spaces" , Lect. notes in math. , 271 , Springer (1972) |
| [4] | S. MacLane, "Categories for the working mathematician" , Springer (1971) |
| [a1] | R. Godement, "Théorie des faisceaux" , Hermann (1958) |
| [a2] | E.G. Manes, "Algebraic theories" , Springer (1976) |
| [a3] | M. Barr, C. Wells, "Toposes, triples and theories" , Springer (1985) |
Standard construction. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Standard_construction&oldid=49442