Difference between revisions of "Motzkin transposition theorem"
m (→Separation theorems: link) |
(correction) |
||
| (One intermediate revision by one other user not shown) | |||
| Line 96: | Line 96: | ||
</span> | </span> | ||
| − | The above results are separation theorems, or statements about the existence of | + | The above results are separation theorems, or statements about the existence of [[hyperplane]]s separating certain disjoint [[convex set]]s. First, some terminology. A set $P\subset\mathbf{R}^n$ is polyhedral (and necessarily convex) if it is the intersection of finitely many closed half-spaces, say |
\begin{equation} P:=\{\mathbf{x}\colon B\mathbf{x}\leq\mathbf{b}\} \end{equation} | \begin{equation} P:=\{\mathbf{x}\colon B\mathbf{x}\leq\mathbf{b}\} \end{equation} | ||
for some matrix $B$ and vector $\mathbf{b}$. | for some matrix $B$ and vector $\mathbf{b}$. | ||
| Line 105: | Line 105: | ||
The dual (or polar) $S^*$ of a non-empty set $S\subset\mathbf{R}^n$ is defined as | The dual (or polar) $S^*$ of a non-empty set $S\subset\mathbf{R}^n$ is defined as | ||
\begin{equation} S^*:=\{\mathbf{y}\colon \mathbf{s}\in S \;\Rightarrow\;\mathbf{y}^T\mathbf{s}\geq 0\}; \end{equation} | \begin{equation} S^*:=\{\mathbf{y}\colon \mathbf{s}\in S \;\Rightarrow\;\mathbf{y}^T\mathbf{s}\geq 0\}; \end{equation} | ||
| − | it is a closed convex cone. In particular, | + | it is a closed [[convex cone]]. In particular, |
\begin{equation}\label{eq:1} \left(\mathbf{R}^+(A)\right)^* =\{\mathbf{y}\colon A^T\mathbf{y}\geq \mathbf{0}\} \end{equation} | \begin{equation}\label{eq:1} \left(\mathbf{R}^+(A)\right)^* =\{\mathbf{y}\colon A^T\mathbf{y}\geq \mathbf{0}\} \end{equation} | ||
| − | is a polyhedral cone. Farkas' theorem b1) states that the vector $\mathbf{b}$ is in the cone $\mathbf{R}^+(A)$. The equivalent statement b2) says that $\mathbf{b}$ cannot be separated from $\mathbf{R}^+(A)$ by a hyperplane: such a separating hyperplane would have a normal $\mathbf{y}$ satisfying | + | is a polyhedral cone. Farkas' theorem b1) states that the vector $\mathbf{b}$ is in the cone $\mathbf{R}^+(A)$. The equivalent statement b2) says that $\mathbf{b}$ cannot be separated from $\mathbf{R}^+(A)$ by a [[hyperplane]]: such a separating hyperplane would have a normal $\mathbf{y}$ satisfying |
\begin{equation} \mathbf{b}^T\mathbf{y} < 0,\quad\mathbf{v}^T\mathbf{y}\geq 0 \end{equation} | \begin{equation} \mathbf{b}^T\mathbf{y} < 0,\quad\mathbf{v}^T\mathbf{y}\geq 0 \end{equation} | ||
for all $\mathbf{v}\in\mathbf{R}^+(A)$ (see e.g. [[#Fig1|Figure 1]]), which by \eqref{eq:1} is a negation of b2). Farkas' theorem for system b) states that for any matrix $A$, | for all $\mathbf{v}\in\mathbf{R}^+(A)$ (see e.g. [[#Fig1|Figure 1]]), which by \eqref{eq:1} is a negation of b2). Farkas' theorem for system b) states that for any matrix $A$, | ||
\begin{equation} \mathbf{R}^+(A)=\left(\mathbf{R}^+(A)\right)^{**} \end{equation} | \begin{equation} \mathbf{R}^+(A)=\left(\mathbf{R}^+(A)\right)^{**} \end{equation} | ||
| − | In general, a set $C\subset\mathbf{R}^n$ is a closed convex cone if and only if $C=C^{**}$. Farkas' theorem for system b) also implies that a cone in $\mathbf{R}^n$ is polyhedral if and only if it is finitely generated (the Farkas–Minkowski–Weyl theorem, [[#References|[a8]]], Corol. 7.1a). More generally, a set $S\subset\mathbf{R}^n$ is polyhedral if and only if it is the sum of a finitely generated cone and the convex hull of finitely many points (the Minkowski–Steinitz–Weyl theorem, [[#References|[a8]]], Corol. 7.1b). | + | In general, a set $C\subset\mathbf{R}^n$ is a closed [[convex cone]] if and only if $C=C^{**}$. Farkas' theorem for system b) also implies that a cone in $\mathbf{R}^n$ is polyhedral if and only if it is finitely generated (the Farkas–Minkowski–Weyl theorem, [[#References|[a8]]], Corol. 7.1a). More generally, a set $S\subset\mathbf{R}^n$ is polyhedral if and only if it is the sum of a finitely generated cone and the [[convex hull]] of finitely many points (the Minkowski–Steinitz–Weyl theorem, [[#References|[a8]]], Corol. 7.1b). |
| − | The theorems of Stiemke and Gordan can be interpreted as geometric statements about intersections $C \cap L$ of a pointed closed convex cone $C$ and a subspace $L$ in $\mathbf{R}^n$. Let $\mathbf{R}^n_{+}$ denote the non-negative orthant in $\mathbf{R}^n$. | + | The theorems of Stiemke and Gordan can be interpreted as geometric statements about intersections $C \cap L$ of a [[Pointed set|pointed]] closed [[convex cone]] $C$ and a subspace $L$ in $\mathbf{R}^n$. Let $\mathbf{R}^n_{+}$ denote the non-negative orthant in $\mathbf{R}^n$. |
Thus, Gordan' theorem d1) says that $\mathbf{R}^n_{+}\cap N(A)\neq\mathbf{0}$, where $N(A)=\{\mathbf{x}\colon A\mathbf{x}=\mathbf{0}\}$ is the null space of $A$. And Stiemke's theorem e1) says that $\mathbf{int}\left(\mathbf{R}^n_{+}\right)\cap N(A)\neq\emptyset$, where $\mathbf{int}\left(\mathbf{R}^n_{+}\right)=\{\mathbf{x}\in\mathbf{R}^n\colon\mathbf{x>0}\}$. | Thus, Gordan' theorem d1) says that $\mathbf{R}^n_{+}\cap N(A)\neq\mathbf{0}$, where $N(A)=\{\mathbf{x}\colon A\mathbf{x}=\mathbf{0}\}$ is the null space of $A$. And Stiemke's theorem e1) says that $\mathbf{int}\left(\mathbf{R}^n_{+}\right)\cap N(A)\neq\emptyset$, where $\mathbf{int}\left(\mathbf{R}^n_{+}\right)=\{\mathbf{x}\in\mathbf{R}^n\colon\mathbf{x>0}\}$. | ||
| Line 138: | Line 138: | ||
<TR><TD valign="top">[a1]</TD> <TD valign="top"> K. Fan, "Systems of linear inequalities" H.W. Kuhn (ed.) A.W. Tucker (ed.) , ''Linear Inequalities and Related Systems'' , ''Ann. of Math. Stud.'' , '''38''' , Princeton Univ. Press (1956,}) pp. 99–156</TD></TR> | <TR><TD valign="top">[a1]</TD> <TD valign="top"> K. Fan, "Systems of linear inequalities" H.W. Kuhn (ed.) A.W. Tucker (ed.) , ''Linear Inequalities and Related Systems'' , ''Ann. of Math. Stud.'' , '''38''' , Princeton Univ. Press (1956,}) pp. 99–156</TD></TR> | ||
<TR><TD valign="top">[a2]</TD> <TD valign="top"> J. Farkas, "Über die Theorie der einfachen Ungleichungen" ''J. Reine Angew. Math.'' , '''124''' (1902) pp. 1–24</TD></TR> | <TR><TD valign="top">[a2]</TD> <TD valign="top"> J. Farkas, "Über die Theorie der einfachen Ungleichungen" ''J. Reine Angew. Math.'' , '''124''' (1902) pp. 1–24</TD></TR> | ||
| − | <TR><TD valign="top">[a3]</TD> <TD valign="top"> P. Gordan, " | + | <TR><TD valign="top">[a3]</TD> <TD valign="top"> P. Gordan, "Ueber die Auflösung linearer Gleichungen mit reellen Coefficienten" ''Math. Ann.'' , '''6''' (1873) pp. 23–28</TD></TR> |
<TR><TD valign="top">[a4]</TD> <TD valign="top"> "Linear inequalities and related systems" H.W. Kuhn (ed.) A.W. Tucker (ed.) , ''Ann. of Math. Stud.'' , '''38''' , Princeton Univ. Press (1956)</TD></TR> | <TR><TD valign="top">[a4]</TD> <TD valign="top"> "Linear inequalities and related systems" H.W. Kuhn (ed.) A.W. Tucker (ed.) , ''Ann. of Math. Stud.'' , '''38''' , Princeton Univ. Press (1956)</TD></TR> | ||
<TR><TD valign="top">[a5]</TD> <TD valign="top"> O.L. Mangasarian, "Nonlinear programming" , McGraw-Hill (1969)</TD></TR> | <TR><TD valign="top">[a5]</TD> <TD valign="top"> O.L. Mangasarian, "Nonlinear programming" , McGraw-Hill (1969)</TD></TR> | ||
Latest revision as of 19:13, 31 March 2017
The thesis of T.S. Motzkin, [a6], in particular his transposition theorem, was a milestone in the development of linear inequalities and related areas.
For two vectors $\mathbf{u} = (u_i)$ and $\mathbf{v} = (v_i)$ of equal dimension one denotes by $\mathbf{u}\geq\mathbf{v}$ and $\mathbf{u}>\mathbf{v}$ that the indicated inequality holds componentwise, and by $\mathbf{u}\gneq\mathbf{v}$ the fact $\mathbf{u}\geq\mathbf{v}$ and $\mathbf{u}\neq\mathbf{v}$.
Systems of linear inequalities appear in several forms; the following examples are typical:
- a) $A\mathbf{x}\leq\mathbf{b}$;
- b) $A\mathbf{x}=\mathbf{b}$, $\mathbf{x}\geq\mathbf{0}$;
- c) $A\mathbf{x}\leq\mathbf{b}$, $B\mathbf{x}<\mathbf{c}$;
- d) $A\mathbf{x}=\mathbf{0}$, $\mathbf{x}\gneq\mathbf{0}$;
- e) $A\mathbf{x}=\mathbf{0}$, $\mathbf{x}>\mathbf{0}$;
- f) $A\mathbf{x}>\mathbf{0}$, $B\mathbf{x}\geq\mathbf{0}$, $C\mathbf{x}=\mathbf{0}$.
In each of these so-called primal systems the existence of solutions is characterized by means of a dual system, using the transposes of matrices in the primal system. Hence the name "transposition theorem" . The relation between the primal and dual systems is sometimes given as a "theorem of alternatives" , listing alternatives, i.e. statements $P$, $Q$ satisfying $P\Leftrightarrow\neg Q$ (where $\neg$ denotes negation), in words: either $P$ or $Q$ but never both.
Relations between a)–f)
a) and b) are equivalent representations. Indeed, they can be written as \begin{equation} (A, -A, I) \begin{pmatrix} \mathbf{x}^+ \\ \mathbf{x}^- \\ \mathbf{s} \end{pmatrix} = \mathbf{b} \quad\text{and}\quad \begin{pmatrix} \mathbf{x}^+ \\ \mathbf{x}^- \\ \mathbf{s} \end{pmatrix} \geq \mathbf{0}, \end{equation} \begin{equation} \begin{pmatrix} A \\ -A \\ -I \end{pmatrix}\mathbf{x}\leq\begin{pmatrix} \mathbf{b} \\ -\mathbf{b} \\ \mathbf{0} \end{pmatrix},\end{equation} respectively.
The remaining systems involve strict inequalities or non-trivial solutions. For example, d) and e) concern the existence of non-trivial solutions and positive solutions, respectively, for the system \begin{equation} A\mathbf{x}=\mathbf{0}, \;\mathbf{x}\geq\mathbf{0}. \end{equation}
Taking $B=0$ and $\mathbf{c}>\mathbf{0}$ in c) gives a), showing that a) and b) are special cases of c). Similarly, the systems d) and e) are special cases of f), which itself is a special case of c) with $\mathbf{b}=\mathbf{0}$, $\mathbf{c}=\mathbf{0}$. In fact, every system of linear inequalities can be written as c).
The following two versions of Motzkin's transposition theorem, [a6], concern systems c) and f):
- (solvability of c)) Given matrices $A$, $B$ and vectors $\mathbf{b}$, $\mathbf{c}$, the following are equivalent:
- c1) the system $A\mathbf{x}\leq\mathbf{b}$, $B\mathbf{x}<\mathbf{c}$ has a solution $\mathbf{x}$;
- c2) for all vectors $\mathbf{y}\geq\mathbf{0}$, $\mathbf{z}\geq\mathbf{0}$, \begin{equation} A^T\mathbf{y}+B^T\mathbf{z}=\mathbf{0} \;\Rightarrow\;\mathbf{b}^T\mathbf{y}+\mathbf{c}^T\mathbf{z}\geq\mathbf{0}. \end{equation} and \begin{equation} A^T\mathbf{y}+B^T\mathbf{z}=\mathbf{0}, \mathbf{z}\neq\mathbf{0} \;\Rightarrow\;\mathbf{b}^T\mathbf{y}+\mathbf{c}^T\mathbf{z}>\mathbf{0}. \end{equation}
- (solvability of f)) Let $A$, $B$, $C$ be given matrices, with $A$ non-vacuous. Then the following are alternatives:
- f1) $A\mathbf{x}>\mathbf{0}$, $B\mathbf{x}\geq\mathbf{0}$, $C\mathbf{x}=\mathbf{0}$ has a solution $\mathbf{x}$;
- f2) $A^T\mathbf{y}_1+B^T\mathbf{y}_2+C^T\mathbf{y}_3=\mathbf{0}$, $\mathbf{y}_1\gneq\mathbf{0}$, $\mathbf{y}_2\geq\mathbf{0}$ has solutions $\mathbf{y}_1$, $\mathbf{y}_2$, $\mathbf{y}_3$.
Special cases of Motzkin's theorem include the following theorems.
Farkas theorem
(See also [a2].) Let $A$ be a given matrix and $\mathbf{b}$ a given vector.
Farkas' theorem for system a) says that the following are equivalent:
- a1) the system $A\mathbf{x}\leq\mathbf{b}$ has a solution $\mathbf{x}$;
- a2) $A^T\mathbf{y}=\mathbf{0}, \;\mathbf{y}\geq\mathbf{0} \;\Rightarrow\; \mathbf{b}^T\mathbf{y}\geq 0$.
Farkas' theorem for system b) says that the following are equivalent:
- b1) the system $A\mathbf{x}=\mathbf{b}$, $\mathbf{x}\geq\mathbf{0}$ has a solution $\mathbf{x}$;
- b2) $A^T\mathbf{y}\geq\mathbf{0} \;\Rightarrow\; \mathbf{b}^T\mathbf{y}\geq 0$.
The positively homogeneous systems d) and e) are covered by the following two theorems.
Gordan's theorem
(See also [a3].) Given a matrix $A$, the following are alternatives:
- d1) $A\mathbf{x}=\mathbf{0}$, $\mathbf{x}\gneq\mathbf{0}$ has a solution $\mathbf{x}$;
- d2) $A^T\mathbf{y}>\mathbf{0}$ has a solution $\mathbf{y}$.
Stiemke's theorem
(See also [a9].) Given a matrix $A$, the following are alternatives:
- e1) $A\mathbf{x}=\mathbf{0}$, $\mathbf{x}>\mathbf{0}$ has a solution $\mathbf{x}$;
- e2) $A^T\mathbf{y}\gneq\mathbf{0}$ has a solution $\mathbf{y}$.
Separation theorems
The above results are separation theorems, or statements about the existence of hyperplanes separating certain disjoint convex sets. First, some terminology. A set $P\subset\mathbf{R}^n$ is polyhedral (and necessarily convex) if it is the intersection of finitely many closed half-spaces, say \begin{equation} P:=\{\mathbf{x}\colon B\mathbf{x}\leq\mathbf{b}\} \end{equation} for some matrix $B$ and vector $\mathbf{b}$.
A finitely generated cone is the set of non-negative linear combinations of finitely many vectors (generators). An example is the cone generated by the columns of a matrix $A$: \begin{equation} \mathbf{R}^+(A):=\{A\mathbf{x}\colon \mathbf{x}\leq\mathbf{0}\} \end{equation}
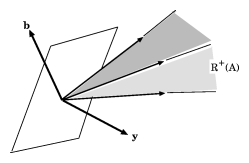
The dual (or polar) $S^*$ of a non-empty set $S\subset\mathbf{R}^n$ is defined as \begin{equation} S^*:=\{\mathbf{y}\colon \mathbf{s}\in S \;\Rightarrow\;\mathbf{y}^T\mathbf{s}\geq 0\}; \end{equation} it is a closed convex cone. In particular, \begin{equation}\label{eq:1} \left(\mathbf{R}^+(A)\right)^* =\{\mathbf{y}\colon A^T\mathbf{y}\geq \mathbf{0}\} \end{equation} is a polyhedral cone. Farkas' theorem b1) states that the vector $\mathbf{b}$ is in the cone $\mathbf{R}^+(A)$. The equivalent statement b2) says that $\mathbf{b}$ cannot be separated from $\mathbf{R}^+(A)$ by a hyperplane: such a separating hyperplane would have a normal $\mathbf{y}$ satisfying \begin{equation} \mathbf{b}^T\mathbf{y} < 0,\quad\mathbf{v}^T\mathbf{y}\geq 0 \end{equation} for all $\mathbf{v}\in\mathbf{R}^+(A)$ (see e.g. Figure 1), which by \eqref{eq:1} is a negation of b2). Farkas' theorem for system b) states that for any matrix $A$, \begin{equation} \mathbf{R}^+(A)=\left(\mathbf{R}^+(A)\right)^{**} \end{equation}
In general, a set $C\subset\mathbf{R}^n$ is a closed convex cone if and only if $C=C^{**}$. Farkas' theorem for system b) also implies that a cone in $\mathbf{R}^n$ is polyhedral if and only if it is finitely generated (the Farkas–Minkowski–Weyl theorem, [a8], Corol. 7.1a). More generally, a set $S\subset\mathbf{R}^n$ is polyhedral if and only if it is the sum of a finitely generated cone and the convex hull of finitely many points (the Minkowski–Steinitz–Weyl theorem, [a8], Corol. 7.1b).
The theorems of Stiemke and Gordan can be interpreted as geometric statements about intersections $C \cap L$ of a pointed closed convex cone $C$ and a subspace $L$ in $\mathbf{R}^n$. Let $\mathbf{R}^n_{+}$ denote the non-negative orthant in $\mathbf{R}^n$.
Thus, Gordan' theorem d1) says that $\mathbf{R}^n_{+}\cap N(A)\neq\mathbf{0}$, where $N(A)=\{\mathbf{x}\colon A\mathbf{x}=\mathbf{0}\}$ is the null space of $A$. And Stiemke's theorem e1) says that $\mathbf{int}\left(\mathbf{R}^n_{+}\right)\cap N(A)\neq\emptyset$, where $\mathbf{int}\left(\mathbf{R}^n_{+}\right)=\{\mathbf{x}\in\mathbf{R}^n\colon\mathbf{x>0}\}$.
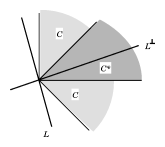
In each case, the dual system uses the intersection $C^* \cap L^\perp$, where $L^\perp$ is the orthogonal complement of $L$. For example, the statements \begin{equation}\label{eq:2} \exists\mathbf{0}\neq\mathbf{x}\in C \cap L \quad\text{and}\quad \exists\mathbf{y}\in\left(\mathbf{int}\,C^*\right) \cap L^\perp \end{equation} are mutually exclusive (see e.g. Figure 2), for otherwise \begin{equation} \mathbf{x}^T\mathbf{y} \begin{cases} =0 & \text{since}\;\mathbf{x}\perp\mathbf{y}, \\ >0 & \text{since}\;\mathbf{0}\neq\mathbf{x}\in C,\;\mathbf{y}\in\mathbf{int}\,C^* . \end{cases}\end{equation}
To make the statements in \eqref{eq:2} alternatives, one has to show that one of them occurs, the hard part of the proof. Returning to the theorems of Gordan and Stiemke, recall that $\left(\mathbf{R}^n_{+}\right)^*=\mathbf{R}^n_{+}$ and $N(A)^\perp=\mathbf{R}(A^T)$. Then Gordan's theorem d1), $\mathbf{R}^n_{+} \cap N(A)\neq\mathbf{0}$, and d2), $\mathbf{int}\left(\mathbf{R}^n_{+}\right)\cap\mathbf{R}(A^T)\neq\emptyset$, are alternatives.
Likewise, Stiemke's theorems e1), $\mathbf{int}\left(\mathbf{R}^n_{+}\right)\cap N(A)\neq\emptyset$, and e2), $\mathbf{R}^n_{+} \cap \mathbf{R}(A^T)\neq\mathbf{0}$, are alternatives.
For history, see [a8], pp. 209–228. For theorems of alternatives, see [a5], pp. 27–37. Generalizations can be found in [a10], [a1], [a11], Sec. 21–22, especially Thm. 21.1; 22.6. Finally, see [a7], [a5], p.100, for applications.
References
| [a1] | K. Fan, "Systems of linear inequalities" H.W. Kuhn (ed.) A.W. Tucker (ed.) , Linear Inequalities and Related Systems , Ann. of Math. Stud. , 38 , Princeton Univ. Press (1956,}) pp. 99–156 |
| [a2] | J. Farkas, "Über die Theorie der einfachen Ungleichungen" J. Reine Angew. Math. , 124 (1902) pp. 1–24 |
| [a3] | P. Gordan, "Ueber die Auflösung linearer Gleichungen mit reellen Coefficienten" Math. Ann. , 6 (1873) pp. 23–28 |
| [a4] | "Linear inequalities and related systems" H.W. Kuhn (ed.) A.W. Tucker (ed.) , Ann. of Math. Stud. , 38 , Princeton Univ. Press (1956) |
| [a5] | O.L. Mangasarian, "Nonlinear programming" , McGraw-Hill (1969) |
| [a6] | T.S. Motzkin, "Beiträge zur Theorie der linearen Ungleichungen" Inaugural Diss. (Basel, Jerusalem) (1936) |
| [a7] | T.S. Motzkin, "Two consequences of the transposition theorem on linear inequalities" Econometrica , 19 (1951) pp. 184–185 |
| [a8] | A. Schrijver, "Theory of linear and integer programming" , Wiley/Interscience (1986) |
| [a9] | E. Stiemke, "Über positive Lösungen homogener linearer Gleichungen" Math. Ann. , 76 (1915) pp. 340–342 |
| [a10] | A.W. Tucker, "Dual systems of homogeneous linear relations" H.W. Kuhn (ed.) A.W. Tucker (ed.) , Linear Inequalities and Related Systems , Ann. of Math. Stud. , 38 , Princeton Univ. Press (1956) pp. 3–18 |
| [a11] | R.T. Rockafellar, "Convex analysis" , Princeton Univ. Press (1970) |
Motzkin transposition theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Motzkin_transposition_theorem&oldid=38651