Difference between revisions of "Brown-Douglas-Fillmore theory"
Ulf Rehmann (talk | contribs) m (moved Brown–Douglas–Fillmore theory to Brown-Douglas-Fillmore theory: ascii title) |
m (Automatically changed introduction) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 88 formulas, 84 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|part}} | ||
''BDF theory'' | ''BDF theory'' | ||
| − | The story of Brown–Douglas–Fillmore theory begins with the Weyl–von Neumann theorem, which, in one of its formulations, says that a bounded [[Self-adjoint operator|self-adjoint operator]] | + | The story of Brown–Douglas–Fillmore theory begins with the Weyl–von Neumann theorem, which, in one of its formulations, says that a bounded [[Self-adjoint operator|self-adjoint operator]] $T = T ^ { * }$ on an infinite-dimensional separable [[Hilbert space|Hilbert space]] $\mathcal{H}$ is determined up to compact perturbations, modulo unitary equivalence, by its essential spectrum. (The essential spectrum is the spectrum $\sigma ( \pi ( T ) )$ of the image $\pi ( T )$ of $T$ in the Calkin algebra $\cal Q ( H ) = B ( H ) / K ( H )$; it is also the spectrum of the restriction of $T$ to the orthogonal complement of the eigenspaces of $T$ for the eigenvalues of finite multiplicity; cf. also [[Spectrum of an operator|Spectrum of an operator]].) In other words, unitary equivalence modulo the compacts $\mathcal{K} ( \mathcal{H} )$ washes out all information about the [[Spectral measure|spectral measure]] of $T$, and only the essential spectrum remains. This result was extended to normal operators (cf. also [[Normal operator|Normal operator]]) by I.D. Berg [[#References|[a4]]] and W. Sikonia [[#References|[a12]]], working independently. However, the theorem is not true for operators that are only essentially normal, in other words, for operators $T$ such that $T T ^ { * } - T ^ { * } T \in \mathcal{K} ( \mathcal{H} )$. Indeed, the "unilateral shift" $S$ satisfies $S ^ { * } S = 1$ and $S S ^ { * } = 1 - P$, where $P$ is a rank-one projection, yet $S$ cannot be a compact perturbation of a normal operator since its Fredholm index (cf. also [[Fredholm-operator(2)|Fredholm operator]]; [[Index of an operator|Index of an operator]]) is non-zero. In [[#References|[a2]]], L.G. Brown, R.G. Douglas and P.A. Fillmore (known to operator theorists as "BDF" ) showed that this is the only obstruction: an operator $T$ in $\mathcal{B} ( \mathcal{H} )$ is a compact perturbation of a normal operator if and only if $T$ is essentially normal and $\operatorname{ind}( T - \lambda ) = 0$ for every $\lambda \notin \sigma ( \pi ( T ) )$. |
| − | However, they went considerably further, by putting this theorem in a | + | However, they went considerably further, by putting this theorem in a $C ^ { * }$-algebraic context in [[#References|[a2]]] and [[#References|[a3]]]. An operator $T$ "up to compact perturbations" defines an injective $*$-homomorphism from a [[C*-algebra|$C ^ { * }$-algebra]] $A$ (the closed subalgebra of $\mathcal{Q} ( \mathcal{H} )$ generated by $\pi ( T )$ and $\pi ( T ^ { * } )$) to $\mathcal{Q} ( \mathcal{H} )$, and the $C ^ { * }$-algebra $A$ is Abelian if and only if $T$ is essentially normal. More generally, an extension of a separable $C ^ { * }$-algebra $A$ is an injective $*$-homomorphism $A \hookrightarrow \mathcal{Q} ( \mathcal{H} )$, since this is equivalent to a commutative diagram with exact rows: |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130270/b13027040.png"/></td> </tr></table> |
| − | BDF defined a natural equivalence relation (basically unitary equivalence) and an addition operation on such extensions, giving a commutative [[Monoid|monoid]] | + | BDF defined a natural equivalence relation (basically unitary equivalence) and an addition operation on such extensions, giving a commutative [[Monoid|monoid]] $\operatorname { Ext } ( A )$, whose $0$-element is represented by split extensions (those for which there is a lifting $A \rightarrow \cal B ( H )$). (The essential uniqueness of the split extensions was shown in [[#References|[a14]]].) It was shown by M.D. Choi and E.G. Effros [[#References|[a6]]] (see also [[#References|[a1]]]) that this monoid is a [[Group|group]] whenever $A$ is nuclear (cf. also [[Nuclear space|Nuclear space]]). (BDF originally worked only with Abelian $C ^ { * }$-algebras $A = C ( X )$, for which this is automatic, and they used the notation $\operatorname { Ext } ( X )$ for $\operatorname { Ext } ( A )$.) BDF showed that $X \mapsto \operatorname { Ext } ( X )$ behaves like a generalized homology theory in $X$ (cf. also [[Generalized cohomology theories|Generalized cohomology theories]]), and in fact for finite CW-complexes (cf. also [[CW-complex|CW-complex]]) coincides with $K _ { 1 } ( X )$, where $K_*$ is the homology theory dual to complex [[K-theory|$K$-theory]]. This was extended in [[#References|[a7]]], where it was shown that $\operatorname { Ext } ( X )$ is canonically isomorphic to $K _ 1 ^ { S } ( X )$, Steenrod $K$-homology (cf. also [[Steenrod–Sitnikov homology|Steenrod–Sitnikov homology]]), for all compact metric spaces $X$, and in [[#References|[a5]]], where it was shown that on a suitable category of $C ^ { * }$-algebras, $\operatorname { Ext } ( A )$ fits into a short [[Exact sequence|exact sequence]] |
| − | + | \begin{equation*} 0 \rightarrow \operatorname { Ext } _ { \mathbf{Z} } ^ { 1 } ( K _ { 0 } ( A ) , \mathbf{Z} ) \rightarrow \operatorname { Ext } ( A ) \rightarrow \end{equation*} | |
| − | + | \begin{equation*} \rightarrow \operatorname{Hom}_{\mathbf{Z}} ( K _ { 1 } ( A ) , \mathbf{Z} ) \rightarrow 0. \end{equation*} | |
| − | It is now (as of 2000) known that BDF theory is just a special case of a more general theory of | + | It is now (as of 2000) known that BDF theory is just a special case of a more general theory of $C ^ { * }$-algebra extensions. One type of generalization (see [[#References|[a13]]]) involves replacing $\mathcal{K} ( \mathcal{H} )$ by the algebra of "compact" operators of a $\mathrm{II} _ { \infty }$ factor (cf. also [[Von Neumann algebra|von Neumann algebra]]). Another sort of generalization involves replacing $\mathcal{K} ( \mathcal{H} )$ by an algebra of the form $B \otimes \mathcal{K} ( \mathcal{H} )$, where $B$ is another separable (or $\sigma$-unital) $C ^ { * }$-algebra. Theories of this sort were worked out in [[#References|[a9]]], [[#References|[a10]]] and in [[#References|[a8]]], though the theory of [[#References|[a9]]], [[#References|[a10]]] turns out to be basically a special case of Kasparov's theory (see [[#References|[a11]]]). Kasparov's <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130270/b13027076.png"/>-theory gives rise to a bivariant functor $\operatorname { Ext } ( A , B )$, and when $A$ is nuclear, this coincides [[#References|[a8]]] with Kasparov's bivariant $K$-functor $K K ^ { 1 } ( A , B )$. |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> W. Arveson, "Notes on extensions of $C ^ { * }$-algebras" ''Duke Math. J.'' , '''44''' : 2 (1977) pp. 329–355</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> L.G. Brown, R.G. Douglas, P.A. Fillmore, "Unitary equivalence modulo the compact operators and extensions of $C ^ { * }$-algebras" , ''Proc. Conf. Operator Theory (Dalhousie Univ., Halifax, N.S., 1973)'' , ''Lecture Notes in Mathematics'' , '''345''' , Springer (1973) pp. 58–128</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> L.G. Brown, R.G. Douglas, P.A. Fillmore, "Extensions of $C ^ { * }$-algebras and $K$-homology" ''Ann. of Math. (2)'' , '''105''' : 2 (1977) pp. 265–324</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> I.D. Berg, "An extension of the Weyl–von Neumann theorem to normal operators" ''Trans. Amer. Math. Soc.'' , '''160''' (1971) pp. 365–371</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> L.G. Brown, "The universal coefficient theorem for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130270/b13027085.png"/> and quasidiagonality" , ''Operator Algebras and Group Representations I (Neptun, 1980)'' , ''Monographs Stud. Math.'' , '''17''' , Pitman (1984) pp. 60–64</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> M.D. Choi, E.G. Effros, "The completely positive lifting problem for $C ^ { * }$-algebras" ''Ann. of Math. (2)'' , '''104''' : 3 (1976) pp. 585–609</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> J. Kaminker, C. Schochet, "$K$-theory and Steenrod homology: applications to the Brown–Douglas–Fillmore theory of operator algebras" ''Trans. Amer. Math. Soc.'' , '''227''' (1977) pp. 63–107</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> G.G. Kasparov, "The operator $K$-functor and extensions of $C ^ { * }$-algebras" ''Math. USSR Izv.'' , '''16''' (1981) pp. 513–572 ''Izv. Akad. Nauk. SSSR Ser. Mat.'' , '''44''' : 3 (1980) pp. 571–636; 719</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> M. Pimsner, S. Popa, D. Voiculescu, "Homogeneous $C ^ { * }$-extensions of $C ( X ) \otimes \mathcal{K} ( H )$. I" ''J. Oper. Th.'' , '''1''' : 1 (1979) pp. 55–108</td></tr><tr><td valign="top">[a10]</td> <td valign="top"> M. Pimsner, S. Popa, D. Voiculescu, "Homogeneous $C ^ { * }$-extensions of $C ( X ) \otimes \mathcal{K} ( H )$. II" ''J. Oper. Th.'' , '''4''' : 2 (1980) pp. 211–249</td></tr><tr><td valign="top">[a11]</td> <td valign="top"> J. Rosenberg, C. Schochet, "Comparing functors classifying extensions of $C ^ { * }$-algebras" ''J. Oper. Th.'' , '''5''' : 2 (1981) pp. 267–282</td></tr><tr><td valign="top">[a12]</td> <td valign="top"> W. Sikonia, "The von Neumann converse of Weyl's theorem" ''Indiana Univ. Math. J.'' , '''21''' (1971/72) pp. 121–124</td></tr><tr><td valign="top">[a13]</td> <td valign="top"> G. Skandalis, "On the group of extensions relative to a semifinite factor" ''J. Oper. Th.'' , '''13''' : 2 (1985) pp. 255–263</td></tr><tr><td valign="top">[a14]</td> <td valign="top"> D. Voiculescu, "A non-commutative Weyl–von Neumann theorem" ''Rev. Roum. Math. Pures Appl.'' , '''21''' : 1 (1976) pp. 97–113</td></tr></table> |
Latest revision as of 17:44, 1 July 2020
BDF theory
The story of Brown–Douglas–Fillmore theory begins with the Weyl–von Neumann theorem, which, in one of its formulations, says that a bounded self-adjoint operator $T = T ^ { * }$ on an infinite-dimensional separable Hilbert space $\mathcal{H}$ is determined up to compact perturbations, modulo unitary equivalence, by its essential spectrum. (The essential spectrum is the spectrum $\sigma ( \pi ( T ) )$ of the image $\pi ( T )$ of $T$ in the Calkin algebra $\cal Q ( H ) = B ( H ) / K ( H )$; it is also the spectrum of the restriction of $T$ to the orthogonal complement of the eigenspaces of $T$ for the eigenvalues of finite multiplicity; cf. also Spectrum of an operator.) In other words, unitary equivalence modulo the compacts $\mathcal{K} ( \mathcal{H} )$ washes out all information about the spectral measure of $T$, and only the essential spectrum remains. This result was extended to normal operators (cf. also Normal operator) by I.D. Berg [a4] and W. Sikonia [a12], working independently. However, the theorem is not true for operators that are only essentially normal, in other words, for operators $T$ such that $T T ^ { * } - T ^ { * } T \in \mathcal{K} ( \mathcal{H} )$. Indeed, the "unilateral shift" $S$ satisfies $S ^ { * } S = 1$ and $S S ^ { * } = 1 - P$, where $P$ is a rank-one projection, yet $S$ cannot be a compact perturbation of a normal operator since its Fredholm index (cf. also Fredholm operator; Index of an operator) is non-zero. In [a2], L.G. Brown, R.G. Douglas and P.A. Fillmore (known to operator theorists as "BDF" ) showed that this is the only obstruction: an operator $T$ in $\mathcal{B} ( \mathcal{H} )$ is a compact perturbation of a normal operator if and only if $T$ is essentially normal and $\operatorname{ind}( T - \lambda ) = 0$ for every $\lambda \notin \sigma ( \pi ( T ) )$.
However, they went considerably further, by putting this theorem in a $C ^ { * }$-algebraic context in [a2] and [a3]. An operator $T$ "up to compact perturbations" defines an injective $*$-homomorphism from a $C ^ { * }$-algebra $A$ (the closed subalgebra of $\mathcal{Q} ( \mathcal{H} )$ generated by $\pi ( T )$ and $\pi ( T ^ { * } )$) to $\mathcal{Q} ( \mathcal{H} )$, and the $C ^ { * }$-algebra $A$ is Abelian if and only if $T$ is essentially normal. More generally, an extension of a separable $C ^ { * }$-algebra $A$ is an injective $*$-homomorphism $A \hookrightarrow \mathcal{Q} ( \mathcal{H} )$, since this is equivalent to a commutative diagram with exact rows:
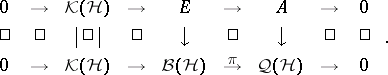 |
BDF defined a natural equivalence relation (basically unitary equivalence) and an addition operation on such extensions, giving a commutative monoid $\operatorname { Ext } ( A )$, whose $0$-element is represented by split extensions (those for which there is a lifting $A \rightarrow \cal B ( H )$). (The essential uniqueness of the split extensions was shown in [a14].) It was shown by M.D. Choi and E.G. Effros [a6] (see also [a1]) that this monoid is a group whenever $A$ is nuclear (cf. also Nuclear space). (BDF originally worked only with Abelian $C ^ { * }$-algebras $A = C ( X )$, for which this is automatic, and they used the notation $\operatorname { Ext } ( X )$ for $\operatorname { Ext } ( A )$.) BDF showed that $X \mapsto \operatorname { Ext } ( X )$ behaves like a generalized homology theory in $X$ (cf. also Generalized cohomology theories), and in fact for finite CW-complexes (cf. also CW-complex) coincides with $K _ { 1 } ( X )$, where $K_*$ is the homology theory dual to complex $K$-theory. This was extended in [a7], where it was shown that $\operatorname { Ext } ( X )$ is canonically isomorphic to $K _ 1 ^ { S } ( X )$, Steenrod $K$-homology (cf. also Steenrod–Sitnikov homology), for all compact metric spaces $X$, and in [a5], where it was shown that on a suitable category of $C ^ { * }$-algebras, $\operatorname { Ext } ( A )$ fits into a short exact sequence
\begin{equation*} 0 \rightarrow \operatorname { Ext } _ { \mathbf{Z} } ^ { 1 } ( K _ { 0 } ( A ) , \mathbf{Z} ) \rightarrow \operatorname { Ext } ( A ) \rightarrow \end{equation*}
\begin{equation*} \rightarrow \operatorname{Hom}_{\mathbf{Z}} ( K _ { 1 } ( A ) , \mathbf{Z} ) \rightarrow 0. \end{equation*}
It is now (as of 2000) known that BDF theory is just a special case of a more general theory of $C ^ { * }$-algebra extensions. One type of generalization (see [a13]) involves replacing $\mathcal{K} ( \mathcal{H} )$ by the algebra of "compact" operators of a $\mathrm{II} _ { \infty }$ factor (cf. also von Neumann algebra). Another sort of generalization involves replacing $\mathcal{K} ( \mathcal{H} )$ by an algebra of the form $B \otimes \mathcal{K} ( \mathcal{H} )$, where $B$ is another separable (or $\sigma$-unital) $C ^ { * }$-algebra. Theories of this sort were worked out in [a9], [a10] and in [a8], though the theory of [a9], [a10] turns out to be basically a special case of Kasparov's theory (see [a11]). Kasparov's  -theory gives rise to a bivariant functor $\operatorname { Ext } ( A , B )$, and when $A$ is nuclear, this coincides [a8] with Kasparov's bivariant $K$-functor $K K ^ { 1 } ( A , B )$.
-theory gives rise to a bivariant functor $\operatorname { Ext } ( A , B )$, and when $A$ is nuclear, this coincides [a8] with Kasparov's bivariant $K$-functor $K K ^ { 1 } ( A , B )$.
References
| [a1] | W. Arveson, "Notes on extensions of $C ^ { * }$-algebras" Duke Math. J. , 44 : 2 (1977) pp. 329–355 |
| [a2] | L.G. Brown, R.G. Douglas, P.A. Fillmore, "Unitary equivalence modulo the compact operators and extensions of $C ^ { * }$-algebras" , Proc. Conf. Operator Theory (Dalhousie Univ., Halifax, N.S., 1973) , Lecture Notes in Mathematics , 345 , Springer (1973) pp. 58–128 |
| [a3] | L.G. Brown, R.G. Douglas, P.A. Fillmore, "Extensions of $C ^ { * }$-algebras and $K$-homology" Ann. of Math. (2) , 105 : 2 (1977) pp. 265–324 |
| [a4] | I.D. Berg, "An extension of the Weyl–von Neumann theorem to normal operators" Trans. Amer. Math. Soc. , 160 (1971) pp. 365–371 |
| [a5] | L.G. Brown, "The universal coefficient theorem for 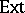 and quasidiagonality" , Operator Algebras and Group Representations I (Neptun, 1980) , Monographs Stud. Math. , 17 , Pitman (1984) pp. 60–64 and quasidiagonality" , Operator Algebras and Group Representations I (Neptun, 1980) , Monographs Stud. Math. , 17 , Pitman (1984) pp. 60–64 |
| [a6] | M.D. Choi, E.G. Effros, "The completely positive lifting problem for $C ^ { * }$-algebras" Ann. of Math. (2) , 104 : 3 (1976) pp. 585–609 |
| [a7] | J. Kaminker, C. Schochet, "$K$-theory and Steenrod homology: applications to the Brown–Douglas–Fillmore theory of operator algebras" Trans. Amer. Math. Soc. , 227 (1977) pp. 63–107 |
| [a8] | G.G. Kasparov, "The operator $K$-functor and extensions of $C ^ { * }$-algebras" Math. USSR Izv. , 16 (1981) pp. 513–572 Izv. Akad. Nauk. SSSR Ser. Mat. , 44 : 3 (1980) pp. 571–636; 719 |
| [a9] | M. Pimsner, S. Popa, D. Voiculescu, "Homogeneous $C ^ { * }$-extensions of $C ( X ) \otimes \mathcal{K} ( H )$. I" J. Oper. Th. , 1 : 1 (1979) pp. 55–108 |
| [a10] | M. Pimsner, S. Popa, D. Voiculescu, "Homogeneous $C ^ { * }$-extensions of $C ( X ) \otimes \mathcal{K} ( H )$. II" J. Oper. Th. , 4 : 2 (1980) pp. 211–249 |
| [a11] | J. Rosenberg, C. Schochet, "Comparing functors classifying extensions of $C ^ { * }$-algebras" J. Oper. Th. , 5 : 2 (1981) pp. 267–282 |
| [a12] | W. Sikonia, "The von Neumann converse of Weyl's theorem" Indiana Univ. Math. J. , 21 (1971/72) pp. 121–124 |
| [a13] | G. Skandalis, "On the group of extensions relative to a semifinite factor" J. Oper. Th. , 13 : 2 (1985) pp. 255–263 |
| [a14] | D. Voiculescu, "A non-commutative Weyl–von Neumann theorem" Rev. Roum. Math. Pures Appl. , 21 : 1 (1976) pp. 97–113 |
Brown-Douglas-Fillmore theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Brown-Douglas-Fillmore_theory&oldid=22195