Difference between revisions of "Braess paradox"
(Importing text file) |
m (corrections) |
||
| (2 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 55 formulas, 52 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|part}} | ||
The words "Braess's paradox" refer to a surprising decrease in performance for some network, which is a result of it being improved locally. The occurrence of this decrease has been studied in mathematical models of equilibrium flow in road/rail traffic, computer networks, telephone networks, water supply systems, electrical circuits, spring systems, and so on. This has been done under various assumptions on routing schemes, such as being state-dependent or fixed. | The words "Braess's paradox" refer to a surprising decrease in performance for some network, which is a result of it being improved locally. The occurrence of this decrease has been studied in mathematical models of equilibrium flow in road/rail traffic, computer networks, telephone networks, water supply systems, electrical circuits, spring systems, and so on. This has been done under various assumptions on routing schemes, such as being state-dependent or fixed. | ||
Below, the occurrence of Braess's paradox in a classical model of user equilibrium traffic flow is given. | Below, the occurrence of Braess's paradox in a classical model of user equilibrium traffic flow is given. | ||
| − | Let | + | Let $( N , B )$ be a finite directed [[Graph|graph]], with node set $N$ and arc, branch or link set $B$ (cf. also [[Graph, oriented|Graph, oriented]]). A path in which all links are similarly directed is called a route, with the initial and final nodes forming an origin/destination pair (or O/D pair). One considers a set $W$ of O/D pairs, and for each $w \in W$, supposes a flow demand $d_{w} > 0$ to be given. Let $R _ { w }$ be a set of routes joining $w$. For each $w \in W$, and $r \in R _ { w }$, one considers $F _ { r } \geq 0$ such that $\sum _ { r \in R _ { W } } F _ { r } = d _ { W }$, giving a route flow vector $F = ( F _ { r } ) _ { r \in R _ { W } , w \in W }$. This route flow induces a link flow $f = ( f _ { b } ) _ { b \in B }$, by $f _ { b } = \sum _ { r \ni b } F _ { r }$ for each $b$, where one identifies a route with the set of its links. For each link $a$, one supposes a link cost <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130210/b13021018.png"/>, where $g _ { ab }$ and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130210/b13021020.png"/> are given. For $r \in R _ { w }$, $w \in W$, one defines a route cost by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130210/b13021023.png"/>. |
| − | A route flow | + | A route flow $H$ is a user equilibrium if it satisfies the condition that for all $r , s \in R _ { w }$, $w \in W$, if $C _ { r } < C _ { s }$ then $H _ { S } = 0$. In other words, there is, for each $w$, a common route cost $\gamma _ { w }$ for all routes $r \in R _ { w }$ with non-zero $H _ { r }$. A user equilibrium flow exists always [[#References|[a5]]], and if the matrix $g = g _ { a b }$ is such that $g + g ^ { T }$ is positive-definite, then the equilibrium link flows, and hence the route costs $\gamma _ { w }$, are unique. In [[#References|[a3]]], Braess's paradox is said to occur if adding a new route $r$ to some $R _ { w }$ results in $\gamma _ { w }$ being increased. See also [[#References|[a3]]] for necessary and sufficient conditions for this to happen under the assumption that there is a strictly positive equilibrium flow in all routes. |
| − | There is no fixed definition of Braess's paradox in all systems, but there is a common theme. One assumes some measure of performance, | + | There is no fixed definition of Braess's paradox in all systems, but there is a common theme. One assumes some measure of performance, $t$, such as $\gamma _ { w }$. On the network given by any one link $b$, $t$ depends on the flow $f$ and a parameter $k_b$. For example, $t = 1 / ( k _ { b } - f )$ if the link is given by an M/M/1 queue (cf. also [[Queue|Queue]]). Note that $t$ decreases if $k_b$ increases, for $f$ fixed. Suppose some flow demand is fixed and link flows are given by some requirement about equilibria, or by a given dynamical process not in equilibrium. One says that Braess's paradox occurs if, for the network as a whole, $t$ increases when some $k_b$ increases. Adding links may be thought of as changing a parameter $k_b$ from zero or infinity. A different language would be used to describe certain other types of networks, such as electrical circuits. |
| − | Under this description, the Downs–Thomson paradox [[#References|[a4]]] is a particular type of Braess's paradox. If one distinguishes these paradoxes mathematically, it is by requiring the link costs | + | Under this description, the Downs–Thomson paradox [[#References|[a4]]] is a particular type of Braess's paradox. If one distinguishes these paradoxes mathematically, it is by requiring the link costs $t$ in the Braess paradox to be increasing functions of the link flow $f$, while in the Downs–Thomson paradox there is a link with $t$ a decreasing function of $f$. |
Independent discoveries of Braess's paradox can be attributed to D. Braess [[#References|[a1]]], A. Downs [[#References|[a4]]], J.M. Thomson [[#References|[a6]]] and C.A. Zukowski and J.L. Wyatt [[#References|[a7]]]. | Independent discoveries of Braess's paradox can be attributed to D. Braess [[#References|[a1]]], A. Downs [[#References|[a4]]], J.M. Thomson [[#References|[a6]]] and C.A. Zukowski and J.L. Wyatt [[#References|[a7]]]. | ||
| Line 16: | Line 24: | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table> |
| + | <tr><td valign="top">[a1]</td> <td valign="top"> D. Braess, "Über ein Paradoxon aus der Verkehrsplannung" ''Unternehmensforschung'' , '''12''' (1968) pp. 258–268</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> D. Braess, ''http://homepage.ruhr-uni-bochum.de/Dietrich.Braess'' (2000)</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> S. Dafermos, A. Nagurney, "On some traffic theory equilibrium paradoxes" ''Transportation Res. B'' , '''18''' (1984) pp. 101–110</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> A. Downs, "The law of peak-hour expressway congestion" ''Traffic Quart.'' , '''16''' (1962) pp. 393–409</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> M.J. Smith, "The existence, uniqueness, and stability of traffic equilibria" ''Transportation Res. B'' , '''13''' (1979) pp. 295–304</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> J.M. Thomson, "Great cities and their traffic" , Gollancz, London (1977)</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> C.A. Zukowski, J.L. Wyatt, "Sensitivity of nonlinear one-port resistor networks" ''IEEE Trans. Circuits Syst.'' , '''CAS-31''' (1984) pp. 1048–1051</td></tr> | ||
| + | </table> | ||
Latest revision as of 15:18, 23 July 2025
The words "Braess's paradox" refer to a surprising decrease in performance for some network, which is a result of it being improved locally. The occurrence of this decrease has been studied in mathematical models of equilibrium flow in road/rail traffic, computer networks, telephone networks, water supply systems, electrical circuits, spring systems, and so on. This has been done under various assumptions on routing schemes, such as being state-dependent or fixed.
Below, the occurrence of Braess's paradox in a classical model of user equilibrium traffic flow is given.
Let $( N , B )$ be a finite directed graph, with node set $N$ and arc, branch or link set $B$ (cf. also Graph, oriented). A path in which all links are similarly directed is called a route, with the initial and final nodes forming an origin/destination pair (or O/D pair). One considers a set $W$ of O/D pairs, and for each $w \in W$, supposes a flow demand $d_{w} > 0$ to be given. Let $R _ { w }$ be a set of routes joining $w$. For each $w \in W$, and $r \in R _ { w }$, one considers $F _ { r } \geq 0$ such that $\sum _ { r \in R _ { W } } F _ { r } = d _ { W }$, giving a route flow vector $F = ( F _ { r } ) _ { r \in R _ { W } , w \in W }$. This route flow induces a link flow $f = ( f _ { b } ) _ { b \in B }$, by $f _ { b } = \sum _ { r \ni b } F _ { r }$ for each $b$, where one identifies a route with the set of its links. For each link $a$, one supposes a link cost 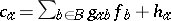 , where $g _ { ab }$ and
, where $g _ { ab }$ and 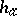 are given. For $r \in R _ { w }$, $w \in W$, one defines a route cost by
are given. For $r \in R _ { w }$, $w \in W$, one defines a route cost by 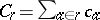 .
.
A route flow $H$ is a user equilibrium if it satisfies the condition that for all $r , s \in R _ { w }$, $w \in W$, if $C _ { r } < C _ { s }$ then $H _ { S } = 0$. In other words, there is, for each $w$, a common route cost $\gamma _ { w }$ for all routes $r \in R _ { w }$ with non-zero $H _ { r }$. A user equilibrium flow exists always [a5], and if the matrix $g = g _ { a b }$ is such that $g + g ^ { T }$ is positive-definite, then the equilibrium link flows, and hence the route costs $\gamma _ { w }$, are unique. In [a3], Braess's paradox is said to occur if adding a new route $r$ to some $R _ { w }$ results in $\gamma _ { w }$ being increased. See also [a3] for necessary and sufficient conditions for this to happen under the assumption that there is a strictly positive equilibrium flow in all routes.
There is no fixed definition of Braess's paradox in all systems, but there is a common theme. One assumes some measure of performance, $t$, such as $\gamma _ { w }$. On the network given by any one link $b$, $t$ depends on the flow $f$ and a parameter $k_b$. For example, $t = 1 / ( k _ { b } - f )$ if the link is given by an M/M/1 queue (cf. also Queue). Note that $t$ decreases if $k_b$ increases, for $f$ fixed. Suppose some flow demand is fixed and link flows are given by some requirement about equilibria, or by a given dynamical process not in equilibrium. One says that Braess's paradox occurs if, for the network as a whole, $t$ increases when some $k_b$ increases. Adding links may be thought of as changing a parameter $k_b$ from zero or infinity. A different language would be used to describe certain other types of networks, such as electrical circuits.
Under this description, the Downs–Thomson paradox [a4] is a particular type of Braess's paradox. If one distinguishes these paradoxes mathematically, it is by requiring the link costs $t$ in the Braess paradox to be increasing functions of the link flow $f$, while in the Downs–Thomson paradox there is a link with $t$ a decreasing function of $f$.
Independent discoveries of Braess's paradox can be attributed to D. Braess [a1], A. Downs [a4], J.M. Thomson [a6] and C.A. Zukowski and J.L. Wyatt [a7].
[a2] contains an ample list of references.
References
| [a1] | D. Braess, "Über ein Paradoxon aus der Verkehrsplannung" Unternehmensforschung , 12 (1968) pp. 258–268 |
| [a2] | D. Braess, http://homepage.ruhr-uni-bochum.de/Dietrich.Braess (2000) |
| [a3] | S. Dafermos, A. Nagurney, "On some traffic theory equilibrium paradoxes" Transportation Res. B , 18 (1984) pp. 101–110 |
| [a4] | A. Downs, "The law of peak-hour expressway congestion" Traffic Quart. , 16 (1962) pp. 393–409 |
| [a5] | M.J. Smith, "The existence, uniqueness, and stability of traffic equilibria" Transportation Res. B , 13 (1979) pp. 295–304 |
| [a6] | J.M. Thomson, "Great cities and their traffic" , Gollancz, London (1977) |
| [a7] | C.A. Zukowski, J.L. Wyatt, "Sensitivity of nonlinear one-port resistor networks" IEEE Trans. Circuits Syst. , CAS-31 (1984) pp. 1048–1051 |
Braess paradox. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Braess_paradox&oldid=16356