|
|
| (One intermediate revision by the same user not shown) |
| Line 1: |
Line 1: |
| − | A number expressible as a fraction of integers. The formal theory of rational numbers is developed using pairs of integers. One considers ordered pairs <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r0776201.png" /> of integers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r0776202.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r0776203.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r0776204.png" />. Two such pairs, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r0776205.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r0776206.png" />, are called equivalent (equal) if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r0776207.png" />. This is an equivalence relation, being reflexive, symmetric and transitive, and so partitions the set of all such pairs into equivalence classes. A rational number is defined as an equivalence class of pairs. A pair <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r0776208.png" /> is also called a rational fraction (or fraction of integers). Distinct classes define distinct rational numbers. The set of all rational numbers is countable. The rational number containing a pair of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r0776209.png" /> is called zero. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762010.png" /> is a rational number and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762011.png" />, then the rational number containing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762012.png" /> is called the (additive) inverse of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762013.png" />, and is denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762014.png" />. A rational number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762015.png" /> is called positive (negative) if it contains a rational fraction <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762016.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762017.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762018.png" /> of the same sign (of different signs). If a rational number is positive (negative), then its (additive) inverse is negative (positive). The set of rational numbers can be ordered in the following way: Every negative rational number is less then every positive one, and a positive rational number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762019.png" /> is less than another positive rational number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762020.png" /> (written <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762021.png" />) if there exist rational fractions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762022.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762023.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762024.png" />, such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762025.png" />; every negative (positive) rational number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762026.png" /> is smaller (greater) then zero: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762027.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762028.png" />); a negative rational number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762029.png" /> is less than another negative rational number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762030.png" /> if the positive rational number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762031.png" /> is greater than the positive rational number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762032.png" />: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762033.png" />. The absolute value <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762034.png" /> of a rational number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762035.png" /> is defined in the usual way: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762036.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762037.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762038.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762039.png" />. | + | {{TEX|done}} |
| | + | A number expressible as a fraction of integers. The formal theory of rational numbers is developed using pairs of integers. One considers ordered pairs $(a,b)$ of integers $a$ and $b$ for which $b\neq0$. Two such pairs, $(a,b)$ and $(c,d)$, are called equivalent (equal) if and only if $ad=bc$. This is an equivalence relation, being reflexive, symmetric and transitive, and so partitions the set of all such pairs into equivalence classes. A rational number is defined as an equivalence class of pairs. A pair $(a,b)$ is also called a rational fraction (or fraction of integers). Distinct classes define distinct rational numbers. The set of all rational numbers is countable. The rational number containing a pair of the form $0/b$ is called zero. If $r$ is a rational number and $a/b\in r$, then the rational number containing $-a/b$ is called the (additive) inverse of $r$, and is denoted by $-r$. A rational number $r$ is called positive (negative) if it contains a rational fraction $a/b$ with $a$ and $b$ of the same sign (of different signs). If a rational number is positive (negative), then its (additive) inverse is negative (positive). The set of rational numbers can be ordered in the following way: Every negative rational number is less then every positive one, and a positive rational number $r'$ is less than another positive rational number $r''$ (written $r'<r''$) if there exist rational fractions $a/b\in r'$ and $c/d\in r''$, $a,b,c,d>0$, such that $ad>bc$; every negative (positive) rational number $r$ is smaller (greater) then zero: $r<0$ ($r>0$); a negative rational number $r'$ is less than another negative rational number $r''$ if the positive rational number $-r'$ is greater than the positive rational number $-r''$: $-r'>-r''$. The absolute value $|r|$ of a rational number $r$ is defined in the usual way: $|r|=r$ if $r\geq0$ and $|r|=-r$ if $r<0$. |
| | | | |
| − | The sum of two rational fractions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762040.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762041.png" /> is defined as the rational fraction <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762042.png" /> and the product as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762043.png" />. The sum and product of two rational numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762044.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762045.png" /> are defined as the equivalence classes of rational fractions containing the sum and product of two rational fractions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762046.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762047.png" /> belonging to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762048.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762049.png" />, respectively. The order, sum and product of rational numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762050.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762051.png" /> do not depend on the choice of representatives of the corresponding equivalence classes, that is, they are uniquely determined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762052.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762053.png" /> themselves. The rational numbers form an [[Ordered field|ordered field]], denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762054.png" />. | + | The sum of two rational fractions $a/b$ and $c/d$ is defined as the rational fraction $(ad+bc)/bd$ and the product as $ac/bd$. The sum and product of two rational numbers $r'$ and $r''$ are defined as the equivalence classes of rational fractions containing the sum and product of two rational fractions $a/b$ and $c/d$ belonging to $r'$ and $r''$, respectively. The order, sum and product of rational numbers $r'$ and $r''$ do not depend on the choice of representatives of the corresponding equivalence classes, that is, they are uniquely determined by $r'$ and $r''$ themselves. The rational numbers form an [[Ordered field|ordered field]], denoted by $\mathbf Q$. |
| | | | |
| − | A rational number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762055.png" /> is denoted by any rational fraction <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762056.png" /> from its equivalence class, i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762057.png" />. Thus, one and the same rational number can be written as distinct, but equivalent, rational fractions. | + | A rational number $r$ is denoted by any rational fraction $a/b$ from its equivalence class, i.e. $a/b\in r$. Thus, one and the same rational number can be written as distinct, but equivalent, rational fractions. |
| | | | |
| − | If every rational number containing a rational fraction of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762058.png" /> is associated with the integer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762059.png" />, then one obtains an isomorphism from the set of such rational numbers onto the ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762060.png" /> of integers. Therefore, the rational number containing a rational fraction of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762061.png" /> is denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762062.png" />. | + | If every rational number containing a rational fraction of the form $a/1$ is associated with the integer $a$, then one obtains an isomorphism from the set of such rational numbers onto the ring $\mathbf Z$ of integers. Therefore, the rational number containing a rational fraction of the form $a/1$ is denoted by $a$. |
| | | | |
| | Each function of the form | | Each function of the form |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762063.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table>
| + | $$\phi(r)=|r|^\alpha,\quad0<\alpha\leq1,\label{1}\tag{1}$$ |
| | | | |
| − | is a norm on the field of rational numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762064.png" />, that is, it satisfies the conditions: | + | is a norm on the field of rational numbers $\mathbf Q$, that is, it satisfies the conditions: |
| | | | |
| − | 1) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762065.png" /> for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762066.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762067.png" />; | + | 1) $\phi(r)>0$ for any $r\neq0$, $\phi(0)=0$; |
| | | | |
| − | 2) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762068.png" />; | + | 2) $\phi(r'+r'')\leq\phi(r')+\phi(r'')$; |
| | | | |
| − | 3) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762069.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762070.png" />. The field of rational numbers is not complete with respect to the norm (1). The completion of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762071.png" /> with respect to the norm (1) yields the field of real numbers. | + | 3) $\phi(r'\cdot r'')=\phi(r')\phi(r'')$ for all $r',r''\in\mathbf Q$. The field of rational numbers is not complete with respect to the norm \eqref{1}. The completion of $\mathbf Q$ with respect to the norm \eqref{1} yields the field of real numbers. |
| | | | |
| | Consider the function | | Consider the function |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762072.png" /></td> <td valign="top" style="width:5%;text-align:right;">(2)</td></tr></table>
| + | $$\Psi_p(r)=\rho^{\nu(r)},\label{2}\tag{2}$$ |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762073.png" /> is a prime number, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762074.png" /> is a rational number and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762075.png" /> is determined by: | + | where $p$ is a prime number, $r$ is a rational number and $\nu(r)$ is determined by: |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762076.png" /></td> </tr></table>
| + | $$r=p^{\nu(r)}\frac ab,$$ |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762077.png" /> is an integer, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762078.png" /> is an irreducible rational fraction such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762079.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762080.png" /> are not divisible by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762081.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762082.png" /> is a fixed number, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762083.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762084.png" /> is a norm on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762085.png" />. It induces the so-called <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762087.png" />-adic metric. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762088.png" /> is not complete with respect to this metric. By completing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762089.png" /> with respect to the norm (2), one obtains the field of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762090.png" />-adic numbers (cf. [[P-adic number|<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762091.png" />-adic number]]). The metrics induced by (1) and (2) (for all prime numbers) exhaust all non-trivial metrics on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762092.png" />. | + | where $\nu(r)$ is an integer, $a/b$ is an irreducible rational fraction such that $a$ and $b$ are not divisible by $p$, and $\rho$ is a fixed number, $0<\rho<1$. Then $\Psi_p$ is a norm on $\mathbf Q$. It induces the so-called $p$-adic metric. $\mathbf Q$ is not complete with respect to this metric. By completing $\mathbf Q$ with respect to the norm \eqref{2}, one obtains the field of $p$-adic numbers (cf. [[P-adic number|$p$-adic number]]). The metrics induced by \eqref{1} and \eqref{2} (for all prime numbers) exhaust all non-trivial metrics on $\mathbf Q$. |
| | | | |
| | In decimal notation, only rational numbers are representable as periodic decimals fractions. | | In decimal notation, only rational numbers are representable as periodic decimals fractions. |
| Line 37: |
Line 38: |
| | | | |
| | ====Comments==== | | ====Comments==== |
| − | Another property characterizing rational numbers is that their [[Continued fraction|continued fraction]] is finite. A very important theme in number theory is to find only the rational solutions of equations such as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762093.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762094.png" />, etc. (see [[Diophantine equations|Diophantine equations]]). Finally, the subject of "rational numbers" is intimately connected with that of irrational numbers (cf. [[Irrational number|Irrational number]]). It is not known, for example, whether or not <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762095.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762096.png" /> or the [[Euler constant|Euler constant]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762097.png" /> are rational. | + | Another property characterizing rational numbers is that their [[Continued fraction|continued fraction]] is finite. A very important theme in number theory is to find only the rational solutions of equations such as $y^2=x^3-7$, $x^3+y^3+z^3=4$, etc. (see [[Diophantine equations|Diophantine equations]]). Finally, the subject of "rational numbers" is intimately connected with that of irrational numbers (cf. [[Irrational number|Irrational number]]). It is not known, for example, whether or not $e\pi$, $e+\pi$ or the [[Euler constant|Euler constant]] $\gamma$ are rational. |
| | | | |
| | ====References==== | | ====References==== |
| | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) pp. Chapt. XIII</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> G. Bachman, "Introduction to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762098.png" />-adic numbers and valuation theory" , Acad. Press (1964)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> B.L. van der Waerden, "Algebra" , '''2''' , Springer (1971) (Translated from German)</TD></TR></table> | | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) pp. Chapt. XIII</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> G. Bachman, "Introduction to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077620/r07762098.png" />-adic numbers and valuation theory" , Acad. Press (1964)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> B.L. van der Waerden, "Algebra" , '''2''' , Springer (1971) (Translated from German)</TD></TR></table> |
A number expressible as a fraction of integers. The formal theory of rational numbers is developed using pairs of integers. One considers ordered pairs $(a,b)$ of integers $a$ and $b$ for which $b\neq0$. Two such pairs, $(a,b)$ and $(c,d)$, are called equivalent (equal) if and only if $ad=bc$. This is an equivalence relation, being reflexive, symmetric and transitive, and so partitions the set of all such pairs into equivalence classes. A rational number is defined as an equivalence class of pairs. A pair $(a,b)$ is also called a rational fraction (or fraction of integers). Distinct classes define distinct rational numbers. The set of all rational numbers is countable. The rational number containing a pair of the form $0/b$ is called zero. If $r$ is a rational number and $a/b\in r$, then the rational number containing $-a/b$ is called the (additive) inverse of $r$, and is denoted by $-r$. A rational number $r$ is called positive (negative) if it contains a rational fraction $a/b$ with $a$ and $b$ of the same sign (of different signs). If a rational number is positive (negative), then its (additive) inverse is negative (positive). The set of rational numbers can be ordered in the following way: Every negative rational number is less then every positive one, and a positive rational number $r'$ is less than another positive rational number $r''$ (written $r'<r''$) if there exist rational fractions $a/b\in r'$ and $c/d\in r''$, $a,b,c,d>0$, such that $ad>bc$; every negative (positive) rational number $r$ is smaller (greater) then zero: $r<0$ ($r>0$); a negative rational number $r'$ is less than another negative rational number $r''$ if the positive rational number $-r'$ is greater than the positive rational number $-r''$: $-r'>-r''$. The absolute value $|r|$ of a rational number $r$ is defined in the usual way: $|r|=r$ if $r\geq0$ and $|r|=-r$ if $r<0$.
The sum of two rational fractions $a/b$ and $c/d$ is defined as the rational fraction $(ad+bc)/bd$ and the product as $ac/bd$. The sum and product of two rational numbers $r'$ and $r''$ are defined as the equivalence classes of rational fractions containing the sum and product of two rational fractions $a/b$ and $c/d$ belonging to $r'$ and $r''$, respectively. The order, sum and product of rational numbers $r'$ and $r''$ do not depend on the choice of representatives of the corresponding equivalence classes, that is, they are uniquely determined by $r'$ and $r''$ themselves. The rational numbers form an ordered field, denoted by $\mathbf Q$.
A rational number $r$ is denoted by any rational fraction $a/b$ from its equivalence class, i.e. $a/b\in r$. Thus, one and the same rational number can be written as distinct, but equivalent, rational fractions.
If every rational number containing a rational fraction of the form $a/1$ is associated with the integer $a$, then one obtains an isomorphism from the set of such rational numbers onto the ring $\mathbf Z$ of integers. Therefore, the rational number containing a rational fraction of the form $a/1$ is denoted by $a$.
Each function of the form
$$\phi(r)=|r|^\alpha,\quad0<\alpha\leq1,\label{1}\tag{1}$$
is a norm on the field of rational numbers $\mathbf Q$, that is, it satisfies the conditions:
1) $\phi(r)>0$ for any $r\neq0$, $\phi(0)=0$;
2) $\phi(r'+r'')\leq\phi(r')+\phi(r'')$;
3) $\phi(r'\cdot r'')=\phi(r')\phi(r'')$ for all $r',r''\in\mathbf Q$. The field of rational numbers is not complete with respect to the norm \eqref{1}. The completion of $\mathbf Q$ with respect to the norm \eqref{1} yields the field of real numbers.
Consider the function
$$\Psi_p(r)=\rho^{\nu(r)},\label{2}\tag{2}$$
where $p$ is a prime number, $r$ is a rational number and $\nu(r)$ is determined by:
$$r=p^{\nu(r)}\frac ab,$$
where $\nu(r)$ is an integer, $a/b$ is an irreducible rational fraction such that $a$ and $b$ are not divisible by $p$, and $\rho$ is a fixed number, $0<\rho<1$. Then $\Psi_p$ is a norm on $\mathbf Q$. It induces the so-called $p$-adic metric. $\mathbf Q$ is not complete with respect to this metric. By completing $\mathbf Q$ with respect to the norm \eqref{2}, one obtains the field of $p$-adic numbers (cf. $p$-adic number). The metrics induced by \eqref{1} and \eqref{2} (for all prime numbers) exhaust all non-trivial metrics on $\mathbf Q$.
In decimal notation, only rational numbers are representable as periodic decimals fractions.
References
| [1] | Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1987) (Translated from Russian) (German translation: Birkhäuser, 1966) |
| [2] | C. Pisot, M. Zamansky, "Mathématiques générales: algèbre-analyse" , Dunod (1966) |
Another property characterizing rational numbers is that their continued fraction is finite. A very important theme in number theory is to find only the rational solutions of equations such as $y^2=x^3-7$, $x^3+y^3+z^3=4$, etc. (see Diophantine equations). Finally, the subject of "rational numbers" is intimately connected with that of irrational numbers (cf. Irrational number). It is not known, for example, whether or not $e\pi$, $e+\pi$ or the Euler constant $\gamma$ are rational.
References
| [a1] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) pp. Chapt. XIII |
| [a2] | G. Bachman, "Introduction to 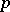 -adic numbers and valuation theory" , Acad. Press (1964) -adic numbers and valuation theory" , Acad. Press (1964) |
| [a3] | B.L. van der Waerden, "Algebra" , 2 , Springer (1971) (Translated from German) |
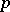 -adic numbers and valuation theory" , Acad. Press (1964)
-adic numbers and valuation theory" , Acad. Press (1964)