Quantile

2020 Mathematics Subject Classification: Primary: 60-01 Secondary: 62-01 [MSN][ZBL]

One of the numerical characteristics of a probability distribution. For a real random variable $X$ with distribution function $F$, by a quantile of order $p$, $0<p<1$, one means the number $K_p$ for which $F(K_p)\leq p$, $F(K_p+0)\geq p$. If $F$ is a continuous strictly-monotone function, then $K_p$ is the unique solution of the equation $F(x)=p$, that is, $K_p$ is the function of $p$ inverse to the function $F$. If $F$ is continuous and $p'>p$, then the probability of the inequality $K_p<X<K_{p'}$, is equal to $p'-p$. The quantile $K_{1/2}$ is the median (in statistics) of the random variable $X$. The quantiles $K_{1/4}$ and $K_{3/4}$ are called the quartiles, and $K_{0.1},\ldots,K_{0.9}$, the deciles. The values of the quantiles for suitable values of $p$ enable one to form an idea about the distribution function.

For example, for the normal distribution (see Fig.)

$$\Phi(x)=\frac{1}{\sqrt{2\pi}}\int\limits_{-\infty}^xe^{-t^2/2}dt$$

the graph of the function $\Phi$ can be drawn from the deciles: $K_{0.1}=-1.28$; $K_{0.2}=-0.84$; $K_{0.3}=-0.52$; $K_{0.4}=-0.25$; $K_{0.5}=0$; $K_{0.6}=0.25$; $K_{0.7}=0.52$; $K_{0.8}=0.84$; $K_{0.9}=1.28$.

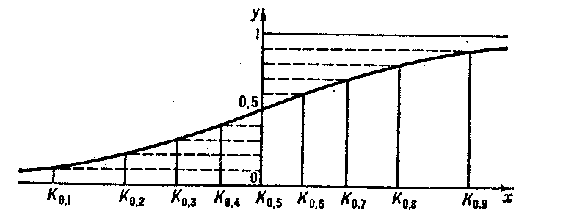
Figure: q076270a

The quartiles of the normal distribution $\Phi$ are $K_{1/4}=-0.67$ and $K_{3/4}=0.67$.

References

[B]	L. Breiman, "Statistics" , Houghton Mifflin (1973) pp. 231ff MR0359089 Zbl 0289.62001
[C]	H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) pp. 181; 367 MR0016588 Zbl 0063.01014