Difference between revisions of "Seifert conjecture"
(Importing text file) |
m (details) |
||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | The assertion that every non-singular (i.e. everywhere non-zero) | + | The assertion that every non-singular (i.e. everywhere non-zero) $C^1$ [[vector field]] on the three-dimensional sphere $S^3$ possesses a circular orbit. |
| − | The conjecture is a three-dimensional analogue of the well-known hairy ball theorem, stating that there is no continuous non-singular vector field on the two-dimensional sphere | + | The conjecture is a three-dimensional analogue of the well-known hairy ball theorem, stating that there is no continuous non-singular vector field on the two-dimensional sphere $S^2$. |
| − | Integrating a | + | Integrating a $C^1$ vector field results in a flow, which on a closed manifold $M$ is a dynamical system, i.e. a mapping $\Phi:\mathbf{R}\times M\to M$ with the properties: |
| − | 1) | + | 1) $\Phi(0,p)=p$; and |
| − | 2) | + | 2) $\Phi(s,\Phi(t,p))=\Phi(t+s,p)$ (the parameter $t$ is usually interpreted as time; cf. also [[Dynamical system|Dynamical system]]; [[Flow (continuous-time dynamical system)|Flow (continuous-time dynamical system)]]). |
| − | An orbit, or a trajectory, of a point | + | An orbit, or a trajectory, of a point $p\in M$ is the set $\Phi(\mathbf{R}\times\{p\})$. If an orbit is simple closed curve, then it is called circular, closed or periodic. |
| − | The [[Hopf fibration|Hopf fibration]] is an [[Essential mapping|essential mapping]] from | + | The [[Hopf fibration|Hopf fibration]] is an [[Essential mapping|essential mapping]] from $S^3$ onto $S^2$ whose fibres, the inverse images of single points, are simple closed curves. The Seifert conjecture has its roots in a 1950 paper of H. Seifert [[#References|[a8]]], who proved that a $C^1$ non-singular vector field on $S^3$ possesses a periodic orbit if it is "almost parallel" to the fibres of the Hopf fibration. |
| − | The even-dimensional spheres do not admit non-singular vector fields, and a higher-dimensional version of the Seifert conjecture for the odd-dimensional spheres has been established in 1966 by F.W. Wilson [[#References|[a9]]] as follows: Any non-singular vector field on a smooth | + | The even-dimensional spheres do not admit non-singular vector fields, and a higher-dimensional version of the Seifert conjecture for the odd-dimensional spheres has been established in 1966 by F.W. Wilson [[#References|[a9]]] as follows: Any non-singular vector field on a smooth $n$-dimensional manifold $M$, $n\geq 3$, can be modified to a vector field with a set of isolated invariant $(n-2)$-tori, $S^1\times...\times S^1$, so that for $p\in M$: |
| − | a) in both cases as | + | a) in both cases as $t\to\infty$ and as $t\to-\infty$, the orbit $\Phi(t,p)$ limits on one of the tori; and |
| − | b) every orbit contained in one of the tori is dense in that torus. Thus, each of the spheres | + | b) every orbit contained in one of the tori is dense in that torus. Thus, each of the spheres $S^5,S^7,...$ admits a non-singular vector field with no circular orbits. |
| − | For his construction, Wilson introduced a plug, a special non-singular vector field on the | + | For his construction, Wilson introduced a plug, a special non-singular vector field on the $n$-dimensional disc $D^n=I\times D^{n-1}$, where $I$ is the unit interval. The plug is constant and parallel to $I\times\{P\}$ on the boundary of $D^n$, and satisfies the trapped-orbit condition and the matched-ends condition (see below). The plug can be inserted in a non-singular vector field on an $n$-dimensional manifold (the mechanism of insertion is illustrated in Fig.a1). |
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/s130200a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/s130200a.gif" /> | ||
| Line 27: | Line 27: | ||
Inserting a plug | Inserting a plug | ||
| − | The trapped-orbit condition guarantees that at least one orbit enters the disc | + | The trapped-orbit condition guarantees that at least one orbit enters the disc $D^n$ at the bottom, $\{0\}\times D^{n-1}$, but never leaves $D^n$. The matched-ends condition means that if an orbit enters the disc $D^n$ at the bottom and leaves $D^n$, then the exit point is the point on $\{1\}\times D^{n-1}$ exactly above the entry point. By appropriately inserting a number of copies of a plug in a vector field on a manifold, Wilson changed the flow so that each orbit starts inside a plug and ends inside one, too. |
| − | In dimension three, Wilson's theorem yields isolated circular orbits and does not resolve the Seifert conjecture. The conjecture remained unsolved until a remarkable construction by P.A. Schweitzer in 1972. His 1974 paper [[#References|[a7]]] describes a three-dimensional plug without periodic orbits, which Schweitzer used to break the isolated periodic orbits, see Fig.a2 and Fig.a3. Inside the plug, instead of circular orbits, there are invariant Denjoy sets to trap the entering orbits. This, initially | + | In dimension three, Wilson's theorem yields isolated circular orbits and does not resolve the Seifert conjecture. The conjecture remained unsolved until a remarkable construction by P.A. Schweitzer in 1972. His 1974 paper [[#References|[a7]]] describes a three-dimensional plug without periodic orbits, which Schweitzer used to break the isolated periodic orbits, see Fig.a2 and Fig.a3. Inside the plug, instead of circular orbits, there are invariant Denjoy sets to trap the entering orbits. This, initially $C^1$, construction was later improved to $C^{2+\delta}$ by J.M. Harrison [[#References|[a3]]]. |
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/s130200b.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/s130200b.gif" /> | ||
| Line 43: | Line 43: | ||
Breaking an orbit | Breaking an orbit | ||
| − | Significant changes to the status of the Seifert conjecture came about in 1993 when H. Hofer [[#References|[a4]]] proved that the Seifert conjecture holds for the Reeb vector field of a contact form on | + | Significant changes to the status of the Seifert conjecture came about in 1993 when H. Hofer [[#References|[a4]]] proved that the Seifert conjecture holds for the Reeb vector field of a contact form on $S^3$ (cf. also [[Contact structure|Contact structure]]). It was the next, after Seifert, advancement in the spirit of the conjecture. |
| − | On the other hand, a | + | On the other hand, a $C^{\infty}$ counterexample to the Seifert conjecture (in its original formulation) was found by K. Kuperberg [[#References|[a5]]] the same year. This aperiodic vector field on $S^3$ also employs a plug. A partial self-insertion performed on a Wilson-type plug breaks the periodic orbits in the plug itself in a recursive process, see Fig.a4. |
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/s130200d.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/s130200d.gif" /> | ||
| Line 55: | Line 55: | ||
The following year, G. Kuperberg [[#References|[a1]]] modified Schweitzer's vector field to a volume-preserving counterexample to the Seifert conjecture, thereby narrowing the gap between the counterexamples and Hofer's theorem. | The following year, G. Kuperberg [[#References|[a1]]] modified Schweitzer's vector field to a volume-preserving counterexample to the Seifert conjecture, thereby narrowing the gap between the counterexamples and Hofer's theorem. | ||
| − | The above constructions generalize to higher dimensions, but counterexamples with stronger properties exist in dimensions above three. The Hamiltonian version of the Seifert conjecture is false for | + | The above constructions generalize to higher dimensions, but counterexamples with stronger properties exist in dimensions above three. The Hamiltonian version of the Seifert conjecture is false for $S^{2n+3}$ for $n\geq1$, as V.L. Ginzburg [[#References|[a2]]] proved that there is a smooth function $H:\mathbf{R}^{2n}\to\mathbf{R}$, $n\geq3$, such that the Hamiltonian flow of $H$ on $\{H=1\}$ has no closed orbits (cf. also [[Hamiltonian system|Hamiltonian system]]). |
==Modified Seifert conjecture.== | ==Modified Seifert conjecture.== | ||
| − | A minimal set of a dynamical system is an invariant, non-empty, compact set containing no proper invariant, non-empty, compact subsets. The modified Seifert conjecture [[#References|[a7]]], [[#References|[a9]]] asserts that every non-singular | + | A minimal set of a dynamical system is an invariant, non-empty, compact set containing no proper invariant, non-empty, compact subsets. The modified Seifert conjecture [[#References|[a7]]], [[#References|[a9]]] asserts that every non-singular $C^1$ vector field on an odd-dimensional sphere $S^{2n+1}$, $n\geq1$, has a minimal set of codimension at least two, i.e. of dimension at most $2n-1$. The invariant sets in the three-dimensional plugs of Wilson and Schweitzer are one-dimensional. In 1996 it was shown [[#References|[a6]]] that the modified Seifert conjecture is false for real-analytic as well as for piecewise-linear flows, for all odd-dimensional spheres: Every non-singular vector field on any manifold can be modified in the given smoothness category so that every minimal set is of codimension one. |
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> G. Kuperberg, "A volume-preserving counterexample to the Seifert conjecture" ''Comment. Math. Helv.'' , '''71''' (1996) pp. 70–97 {{MR|1371679}} {{ZBL|0859.57017}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> V.L. Ginzburg, "A smooth counterexample to the Hamiltonian Seifert conjecture in $R^6$" ''Internat. Math. Res. Notices'' , '''13''' (1997) pp. 641–650 {{MR|1459629}} {{ZBL|0913.58022}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J. Harrison, "$C^2$ counterexamples to the Seifert conjecture" ''Topology'' , '''27''' (1988) pp. 249–278 {{MR|0963630}} {{ZBL|0669.57011}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> H. Hofer, "Pseudoholomorphic curves in symplectizations with applications to the Weinstein conjecture in dimension three" ''Invent. Math.'' , '''114''' (1993) pp. 515–563 {{MR|1244912}} {{ZBL|0797.58023}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> K. Kuperberg, "A smooth counterexample to the Seifert conjecture" ''Ann. of Math.'' , '''140''' (1994) pp. 723–732 {{MR|1307902}} {{ZBL|0856.57024}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> G. Kuperberg, K. Kuperberg, "Generalized counterexamples to the Seifert conjecture" ''Ann. of Math.'' , '''144''' (1996) pp. 239–268 {{MR|1418899}} {{MR|1394969}} {{ZBL|0856.57026}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> P.A. Schweitzer, "Counterexamples to the Seifert conjecture and opening closed leaves of foliations" ''Ann. of Math.'' , '''100''' (1974) pp. 386–400 {{MR|0356086}} {{ZBL|0295.57010}} </TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> H. Seifert, "Closed integral curves in $3$-space and isotopic two-dimensional deformations" ''Proc. Amer. Math. Soc.'' , '''1''' (1950) pp. 287–302 {{MR|37508}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> F.W. Wilson, "On the minimal sets of non-singular vector fields" ''Ann. of Math.'' , '''84''' (1966) pp. 529–536 {{MR|0202155}} {{ZBL|0156.43803}} </TD></TR></table> |
Latest revision as of 17:40, 17 March 2024
The assertion that every non-singular (i.e. everywhere non-zero) $C^1$ vector field on the three-dimensional sphere $S^3$ possesses a circular orbit.
The conjecture is a three-dimensional analogue of the well-known hairy ball theorem, stating that there is no continuous non-singular vector field on the two-dimensional sphere $S^2$.
Integrating a $C^1$ vector field results in a flow, which on a closed manifold $M$ is a dynamical system, i.e. a mapping $\Phi:\mathbf{R}\times M\to M$ with the properties:
1) $\Phi(0,p)=p$; and
2) $\Phi(s,\Phi(t,p))=\Phi(t+s,p)$ (the parameter $t$ is usually interpreted as time; cf. also Dynamical system; Flow (continuous-time dynamical system)).
An orbit, or a trajectory, of a point $p\in M$ is the set $\Phi(\mathbf{R}\times\{p\})$. If an orbit is simple closed curve, then it is called circular, closed or periodic.
The Hopf fibration is an essential mapping from $S^3$ onto $S^2$ whose fibres, the inverse images of single points, are simple closed curves. The Seifert conjecture has its roots in a 1950 paper of H. Seifert [a8], who proved that a $C^1$ non-singular vector field on $S^3$ possesses a periodic orbit if it is "almost parallel" to the fibres of the Hopf fibration.
The even-dimensional spheres do not admit non-singular vector fields, and a higher-dimensional version of the Seifert conjecture for the odd-dimensional spheres has been established in 1966 by F.W. Wilson [a9] as follows: Any non-singular vector field on a smooth $n$-dimensional manifold $M$, $n\geq 3$, can be modified to a vector field with a set of isolated invariant $(n-2)$-tori, $S^1\times...\times S^1$, so that for $p\in M$:
a) in both cases as $t\to\infty$ and as $t\to-\infty$, the orbit $\Phi(t,p)$ limits on one of the tori; and
b) every orbit contained in one of the tori is dense in that torus. Thus, each of the spheres $S^5,S^7,...$ admits a non-singular vector field with no circular orbits.
For his construction, Wilson introduced a plug, a special non-singular vector field on the $n$-dimensional disc $D^n=I\times D^{n-1}$, where $I$ is the unit interval. The plug is constant and parallel to $I\times\{P\}$ on the boundary of $D^n$, and satisfies the trapped-orbit condition and the matched-ends condition (see below). The plug can be inserted in a non-singular vector field on an $n$-dimensional manifold (the mechanism of insertion is illustrated in Fig.a1).
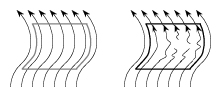
Figure: s130200a
Inserting a plug
The trapped-orbit condition guarantees that at least one orbit enters the disc $D^n$ at the bottom, $\{0\}\times D^{n-1}$, but never leaves $D^n$. The matched-ends condition means that if an orbit enters the disc $D^n$ at the bottom and leaves $D^n$, then the exit point is the point on $\{1\}\times D^{n-1}$ exactly above the entry point. By appropriately inserting a number of copies of a plug in a vector field on a manifold, Wilson changed the flow so that each orbit starts inside a plug and ends inside one, too.
In dimension three, Wilson's theorem yields isolated circular orbits and does not resolve the Seifert conjecture. The conjecture remained unsolved until a remarkable construction by P.A. Schweitzer in 1972. His 1974 paper [a7] describes a three-dimensional plug without periodic orbits, which Schweitzer used to break the isolated periodic orbits, see Fig.a2 and Fig.a3. Inside the plug, instead of circular orbits, there are invariant Denjoy sets to trap the entering orbits. This, initially $C^1$, construction was later improved to $C^{2+\delta}$ by J.M. Harrison [a3].
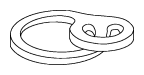
Figure: s130200b
Schweitzer's plug
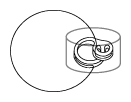
Figure: s130200c
Breaking an orbit
Significant changes to the status of the Seifert conjecture came about in 1993 when H. Hofer [a4] proved that the Seifert conjecture holds for the Reeb vector field of a contact form on $S^3$ (cf. also Contact structure). It was the next, after Seifert, advancement in the spirit of the conjecture.
On the other hand, a $C^{\infty}$ counterexample to the Seifert conjecture (in its original formulation) was found by K. Kuperberg [a5] the same year. This aperiodic vector field on $S^3$ also employs a plug. A partial self-insertion performed on a Wilson-type plug breaks the periodic orbits in the plug itself in a recursive process, see Fig.a4.
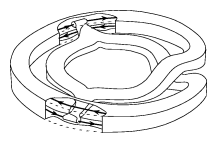
Figure: s130200d
The K-plug — a self-inserted Wilson plug
The following year, G. Kuperberg [a1] modified Schweitzer's vector field to a volume-preserving counterexample to the Seifert conjecture, thereby narrowing the gap between the counterexamples and Hofer's theorem.
The above constructions generalize to higher dimensions, but counterexamples with stronger properties exist in dimensions above three. The Hamiltonian version of the Seifert conjecture is false for $S^{2n+3}$ for $n\geq1$, as V.L. Ginzburg [a2] proved that there is a smooth function $H:\mathbf{R}^{2n}\to\mathbf{R}$, $n\geq3$, such that the Hamiltonian flow of $H$ on $\{H=1\}$ has no closed orbits (cf. also Hamiltonian system).
Modified Seifert conjecture.
A minimal set of a dynamical system is an invariant, non-empty, compact set containing no proper invariant, non-empty, compact subsets. The modified Seifert conjecture [a7], [a9] asserts that every non-singular $C^1$ vector field on an odd-dimensional sphere $S^{2n+1}$, $n\geq1$, has a minimal set of codimension at least two, i.e. of dimension at most $2n-1$. The invariant sets in the three-dimensional plugs of Wilson and Schweitzer are one-dimensional. In 1996 it was shown [a6] that the modified Seifert conjecture is false for real-analytic as well as for piecewise-linear flows, for all odd-dimensional spheres: Every non-singular vector field on any manifold can be modified in the given smoothness category so that every minimal set is of codimension one.
References
| [a1] | G. Kuperberg, "A volume-preserving counterexample to the Seifert conjecture" Comment. Math. Helv. , 71 (1996) pp. 70–97 MR1371679 Zbl 0859.57017 |
| [a2] | V.L. Ginzburg, "A smooth counterexample to the Hamiltonian Seifert conjecture in $R^6$" Internat. Math. Res. Notices , 13 (1997) pp. 641–650 MR1459629 Zbl 0913.58022 |
| [a3] | J. Harrison, "$C^2$ counterexamples to the Seifert conjecture" Topology , 27 (1988) pp. 249–278 MR0963630 Zbl 0669.57011 |
| [a4] | H. Hofer, "Pseudoholomorphic curves in symplectizations with applications to the Weinstein conjecture in dimension three" Invent. Math. , 114 (1993) pp. 515–563 MR1244912 Zbl 0797.58023 |
| [a5] | K. Kuperberg, "A smooth counterexample to the Seifert conjecture" Ann. of Math. , 140 (1994) pp. 723–732 MR1307902 Zbl 0856.57024 |
| [a6] | G. Kuperberg, K. Kuperberg, "Generalized counterexamples to the Seifert conjecture" Ann. of Math. , 144 (1996) pp. 239–268 MR1418899 MR1394969 Zbl 0856.57026 |
| [a7] | P.A. Schweitzer, "Counterexamples to the Seifert conjecture and opening closed leaves of foliations" Ann. of Math. , 100 (1974) pp. 386–400 MR0356086 Zbl 0295.57010 |
| [a8] | H. Seifert, "Closed integral curves in $3$-space and isotopic two-dimensional deformations" Proc. Amer. Math. Soc. , 1 (1950) pp. 287–302 MR37508 |
| [a9] | F.W. Wilson, "On the minimal sets of non-singular vector fields" Ann. of Math. , 84 (1966) pp. 529–536 MR0202155 Zbl 0156.43803 |
Seifert conjecture. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Seifert_conjecture&oldid=12487