Difference between revisions of "VMOA-space"
m (AUTOMATIC EDIT (latexlist): Replaced 14 formulas out of 25 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
m (Automatically changed introduction) |
||
| Line 2: | Line 2: | ||
the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
was used. | was used. | ||
| − | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. |
Out of 25 formulas, 14 were replaced by TEX code.--> | Out of 25 formulas, 14 were replaced by TEX code.--> | ||
| − | {{TEX|semi-auto}}{{TEX| | + | {{TEX|semi-auto}}{{TEX|part}} |
''space of analytic functions of vanishing mean oscillation'' | ''space of analytic functions of vanishing mean oscillation'' | ||
Latest revision as of 17:47, 1 July 2020
space of analytic functions of vanishing mean oscillation
The class of analytic functions on the unit disc that are in  (see also $\operatorname{BMO}$-space;
(see also $\operatorname{BMO}$-space;  -space;
-space;  -space).
-space).
Fefferman's duality theorem (see $\operatorname{BMO}$-space) gives the characterization that an analytic function in $\operatorname{BMO}$ is in  if and only if its boundary values can be expressed as the sum of a continuous function and the harmonic conjugate (cf. also Harmonic function) of a continuous function. This suggests that functions in
if and only if its boundary values can be expressed as the sum of a continuous function and the harmonic conjugate (cf. also Harmonic function) of a continuous function. This suggests that functions in  are close to being continuous, but one has to be careful because their behaviour can be quite wild. For example, it can be show that any conformal mapping onto a region of finite area is in
are close to being continuous, but one has to be careful because their behaviour can be quite wild. For example, it can be show that any conformal mapping onto a region of finite area is in  .
.
D. Sarason [a5] used the fact that  is the closure of the disc algebra $A$ in
is the closure of the disc algebra $A$ in 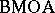 to prove that $H ^ { \infty } + C$, with $C$ the class of continuous functions, is a closed subalgebra of $L^{\infty}$ and consequently the simplest example of a Douglas algebra (see
to prove that $H ^ { \infty } + C$, with $C$ the class of continuous functions, is a closed subalgebra of $L^{\infty}$ and consequently the simplest example of a Douglas algebra (see 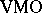 -space).
-space).
The distance between a function $f$ in 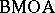 and
and 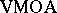 has attracted some interest, [a1], [a2], [a4]. Let $f$ be an analytic function on the unit disc, $\zeta$ a point on the boundary $T$ and write $K _ { \zeta }$ for the cluster set $\operatorname{Cl} ( f , \zeta )$. Using an assortment of tools from functional analysis, S. Axler and J. Shapiro [a1] proved that
has attracted some interest, [a1], [a2], [a4]. Let $f$ be an analytic function on the unit disc, $\zeta$ a point on the boundary $T$ and write $K _ { \zeta }$ for the cluster set $\operatorname{Cl} ( f , \zeta )$. Using an assortment of tools from functional analysis, S. Axler and J. Shapiro [a1] proved that
\begin{equation*} \| f + \operatorname {VMOA} \| _ { * } \leq C \operatorname { lim sup } _ { \zeta \in T } \sqrt { \operatorname { area } ( K _ { \zeta } ) }. \end{equation*}
This led to a search for the optimal geometric condition for the right-hand side above, see [a4] for the answer.
References
| [a1] | S. Axler, J. Shapiro, "Putnam's theorem, Alexander's spectral area estimate and VMO" Math. Ann. , 271 (1985) pp. 161–183 |
| [a2] | J. Carmona, J. Cufi, "On the distance of an analytic function to VMO" J. London Math. Soc. (2) , 34 (1986) pp. 52–66 |
| [a3] | C. Fefferman, "Characterization of bounded mean oscillation" Bull. Amer. Math. Soc. , 77 (1971) pp. 587–588 |
| [a4] | K. Stephenson, D. Stegenga, "Sharp geometric estimates of the distance to VMOA" Contemp. Math. , 137 (1992) pp. 421–432 |
| [a5] | D. Sarason, "Functions of vanishing mean oscillation" Trans. Amer. Math. Soc. , 207 (1975) pp. 391–405 |
VMOA-space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=VMOA-space&oldid=50357