Difference between revisions of "Fenchel-Moreau conjugate function"
Ulf Rehmann (talk | contribs) m (moved Fenchel–Moreau conjugate function to Fenchel-Moreau conjugate function: ascii title) |
m (Automatically changed introduction) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 52 formulas, 49 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|part}} | |
| + | Given two sets $X$, $W$ and a "coupling" function $\varphi : X \times W \rightarrow \overline { \mathbf{R} }$, the Fenchel–Moreau conjugate to a function $f : X \rightarrow \overline { \mathbf{R} }$ with respect to the coupling function $\varphi$ is the function $f ^ { c \langle \varphi \rangle } : W \rightarrow \overline { \mathbf{R} }$ defined by | ||
| − | + | \begin{equation} \tag{a1} f ^ { c ( \varphi ) } ( w ) = \operatorname { sup } _ { x \in X } \{ \varphi ( x , w ) - f ( x ) \} ( w \in W ), \end{equation} | |
| − | <table class="eq" style="width:100%;"> <tr><td | + | with the convention $( + \infty ) - ( + \infty ) = - \infty - ( - \infty ) = - \infty$ [[#References|[a1]]]. When $X$ and $W$ are linear spaces in duality, via a bilinear coupling function $\varphi$ (cf. also [[Linear space|Linear space]]; [[Duality|Duality]]), $f ^ { c ( \varphi )}$ is just the usual Fenchel conjugate $f ^ { * }$ (called also the Young–Fenchel conjugate, or Legendre–Fenchel conjugate; cf. also [[Legendre transform|Legendre transform]]) of $f$. If $X$ is a [[Locally convex space|locally convex space]] and $W = X ^ { * },$ the conjugate space of $X$, with the coupling function $\varphi ( x , w ) = w ( x )$, then the second Fenchel conjugate $f ^ { * * } = ( f ^ { * } ) ^ { * }$ of $f$ coincides with the greatest lower semi-continuous minorant of $f$ (Moreau's theorem); this result admits a natural extension to Fenchel–Moreau conjugates $f ^ { c ( \varphi )}$. |
| + | |||
| + | Another important particular class of Fenchel–Moreau conjugates is obtained for coupling functions $\varphi : X \times W \rightarrow \overline { \mathbf{R} }$ that take only the values $0$ and $- \infty,$ or, equivalently, the conjugates for which there exists a (unique) subset $\Omega$ of $X \times W$ such that | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120040/f12004028.png"/></td> <td style="width:5%;text-align:right;" valign="top">(a2)</td></tr></table> | ||
these are called conjugates of type Lau or level-set conjugates. While Fenchel conjugates have many applications in [[Convex analysis|convex analysis]], conjugates of type Lau are useful for the study of quasi-convex functions (i.e., of functions all of whose level sets are convex) and for duality theory in micro-economics (duality between direct and indirect utility functions). | these are called conjugates of type Lau or level-set conjugates. While Fenchel conjugates have many applications in [[Convex analysis|convex analysis]], conjugates of type Lau are useful for the study of quasi-convex functions (i.e., of functions all of whose level sets are convex) and for duality theory in micro-economics (duality between direct and indirect utility functions). | ||
| − | A useful related concept is the Flachs–Pollatschek conjugate function | + | A useful related concept is the Flachs–Pollatschek conjugate function $f ^ { \Delta ( \varphi ) } : W \rightarrow \overline {\bf R }$, defined by |
| − | + | \begin{equation} \tag{a3} f ^ { \Delta ( \varphi ) } ( w ) = \operatorname { sup } _ { x \in X } \operatorname { min } \{ \varphi ( x , w ) , - f ( x ) \} ( w \in W ), \end{equation} | |
which has applications in, e.g., optimization theory. | which has applications in, e.g., optimization theory. | ||
| − | A unified approach is the conjugate function with respect to a binary operation | + | A unified approach is the conjugate function with respect to a binary operation $\odot$ on $\overline{\mathbf{R}}$, assumed completely distributive (cf. also [[Completely distributive lattice|Completely distributive lattice]]) with respect to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120040/f12004033.png"/> in the [[Lattice|lattice]] $( \overline { \mathbf{R} } , \leq )$, defined by |
| − | + | \begin{equation} \tag{a4} f ^ { b ( \varphi ) } ( w ) = \operatorname { sup } _ { x \in X } \{ - [ - \varphi ( x , w ) \odot f ( x ) ] \} ( w \in W ); \end{equation} | |
| − | in particular, when | + | in particular, when $\odot = +$ (respectively, $\odot=\max$), $f ^ { b ( \varphi ) }$ is the Fenchel–Moreau (respectively, the Flachs–Pollatschek) conjugate function of $f$. |
| − | In another direction, the Fenchel–Moreau conjugate has been generalized to functions with values in extensions | + | In another direction, the Fenchel–Moreau conjugate has been generalized to functions with values in extensions $\overline { G }$ of ordered groups $G$, with applications to functions in the extension (by adjoining $- \infty$ and $+ \infty$) of the additive group $( \mathbf{R} , + , \leq )$ and to functions in the extension (by adjoining $0$ and $+ \infty$) of the multiplicative group $( \mathbf{R} _ { + } \backslash \{ 0 \} , \times , \leq )$. More generally, one has also defined the conjugate function of $f : X \rightarrow \overline { G }$ with respect to a binary operation $\odot$ on $\overline { G }$, encompassing the preceding conjugates as particular cases. |
| − | One of the main fields of applications of these concepts is optimization theory: When | + | One of the main fields of applications of these concepts is optimization theory: When $f$ is the [[Objective function|objective function]] of an optimization problem, a conjugate function is used to define (the objective function of) a "dual" optimization problem. |
For more details, see [[#References|[a2]]], [[#References|[a3]]], [[#References|[a4]]]. | For more details, see [[#References|[a2]]], [[#References|[a3]]], [[#References|[a4]]]. | ||
| Line 32: | Line 40: | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> J.-J. Moreau, "Fonctions convexes en dualité" , Univ. Montpellier (1962)</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> J. Flachs, M.A. Pollatschek, "Duality theorems for certain programs involving minimum or maximum operations" ''Math. Progr.'' , '''16''' (1979) pp. 348–370</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> W.E. Diewert, "Duality approaches to microeconomic theory" K.J. Arrow (ed.) M.D. Intrilligator (ed.) , ''Handbook of Mathematical Economics'' , '''2''' , North-Holland (1982) pp. 535–599</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> I. Singer, "Abstract convex analysis" , Wiley–Interscience (1997)</td></tr></table> |
Latest revision as of 17:44, 1 July 2020
Given two sets $X$, $W$ and a "coupling" function $\varphi : X \times W \rightarrow \overline { \mathbf{R} }$, the Fenchel–Moreau conjugate to a function $f : X \rightarrow \overline { \mathbf{R} }$ with respect to the coupling function $\varphi$ is the function $f ^ { c \langle \varphi \rangle } : W \rightarrow \overline { \mathbf{R} }$ defined by
\begin{equation} \tag{a1} f ^ { c ( \varphi ) } ( w ) = \operatorname { sup } _ { x \in X } \{ \varphi ( x , w ) - f ( x ) \} ( w \in W ), \end{equation}
with the convention $( + \infty ) - ( + \infty ) = - \infty - ( - \infty ) = - \infty$ [a1]. When $X$ and $W$ are linear spaces in duality, via a bilinear coupling function $\varphi$ (cf. also Linear space; Duality), $f ^ { c ( \varphi )}$ is just the usual Fenchel conjugate $f ^ { * }$ (called also the Young–Fenchel conjugate, or Legendre–Fenchel conjugate; cf. also Legendre transform) of $f$. If $X$ is a locally convex space and $W = X ^ { * },$ the conjugate space of $X$, with the coupling function $\varphi ( x , w ) = w ( x )$, then the second Fenchel conjugate $f ^ { * * } = ( f ^ { * } ) ^ { * }$ of $f$ coincides with the greatest lower semi-continuous minorant of $f$ (Moreau's theorem); this result admits a natural extension to Fenchel–Moreau conjugates $f ^ { c ( \varphi )}$.
Another important particular class of Fenchel–Moreau conjugates is obtained for coupling functions $\varphi : X \times W \rightarrow \overline { \mathbf{R} }$ that take only the values $0$ and $- \infty,$ or, equivalently, the conjugates for which there exists a (unique) subset $\Omega$ of $X \times W$ such that
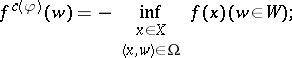 | (a2) |
these are called conjugates of type Lau or level-set conjugates. While Fenchel conjugates have many applications in convex analysis, conjugates of type Lau are useful for the study of quasi-convex functions (i.e., of functions all of whose level sets are convex) and for duality theory in micro-economics (duality between direct and indirect utility functions).
A useful related concept is the Flachs–Pollatschek conjugate function $f ^ { \Delta ( \varphi ) } : W \rightarrow \overline {\bf R }$, defined by
\begin{equation} \tag{a3} f ^ { \Delta ( \varphi ) } ( w ) = \operatorname { sup } _ { x \in X } \operatorname { min } \{ \varphi ( x , w ) , - f ( x ) \} ( w \in W ), \end{equation}
which has applications in, e.g., optimization theory.
A unified approach is the conjugate function with respect to a binary operation $\odot$ on $\overline{\mathbf{R}}$, assumed completely distributive (cf. also Completely distributive lattice) with respect to 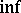 in the lattice $( \overline { \mathbf{R} } , \leq )$, defined by
in the lattice $( \overline { \mathbf{R} } , \leq )$, defined by
\begin{equation} \tag{a4} f ^ { b ( \varphi ) } ( w ) = \operatorname { sup } _ { x \in X } \{ - [ - \varphi ( x , w ) \odot f ( x ) ] \} ( w \in W ); \end{equation}
in particular, when $\odot = +$ (respectively, $\odot=\max$), $f ^ { b ( \varphi ) }$ is the Fenchel–Moreau (respectively, the Flachs–Pollatschek) conjugate function of $f$.
In another direction, the Fenchel–Moreau conjugate has been generalized to functions with values in extensions $\overline { G }$ of ordered groups $G$, with applications to functions in the extension (by adjoining $- \infty$ and $+ \infty$) of the additive group $( \mathbf{R} , + , \leq )$ and to functions in the extension (by adjoining $0$ and $+ \infty$) of the multiplicative group $( \mathbf{R} _ { + } \backslash \{ 0 \} , \times , \leq )$. More generally, one has also defined the conjugate function of $f : X \rightarrow \overline { G }$ with respect to a binary operation $\odot$ on $\overline { G }$, encompassing the preceding conjugates as particular cases.
One of the main fields of applications of these concepts is optimization theory: When $f$ is the objective function of an optimization problem, a conjugate function is used to define (the objective function of) a "dual" optimization problem.
For more details, see [a2], [a3], [a4].
See also Conjugate function; Dual functions.
References
| [a1] | J.-J. Moreau, "Fonctions convexes en dualité" , Univ. Montpellier (1962) |
| [a2] | J. Flachs, M.A. Pollatschek, "Duality theorems for certain programs involving minimum or maximum operations" Math. Progr. , 16 (1979) pp. 348–370 |
| [a3] | W.E. Diewert, "Duality approaches to microeconomic theory" K.J. Arrow (ed.) M.D. Intrilligator (ed.) , Handbook of Mathematical Economics , 2 , North-Holland (1982) pp. 535–599 |
| [a4] | I. Singer, "Abstract convex analysis" , Wiley–Interscience (1997) |
Fenchel-Moreau conjugate function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fenchel-Moreau_conjugate_function&oldid=22415