Difference between revisions of "Santaló formula"
Ulf Rehmann (talk | contribs) m (moved Santalo formula to Santaló formula over redirect: accented title) |
m (AUTOMATIC EDIT (latexlist): Replaced 49 formulas out of 51 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 51 formulas, 49 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|partial}} | ||
A formula describing the Liouville measure on the unit tangent bundle of a [[Riemannian manifold|Riemannian manifold]] in terms of the [[Geodesic flow|geodesic flow]] and the measure of a codimension-one submanifold (see [[#References|[a5]]] and [[#References|[a6]]], Chap. 19). | A formula describing the Liouville measure on the unit tangent bundle of a [[Riemannian manifold|Riemannian manifold]] in terms of the [[Geodesic flow|geodesic flow]] and the measure of a codimension-one submanifold (see [[#References|[a5]]] and [[#References|[a6]]], Chap. 19). | ||
| − | Let | + | Let $M$ be an $n$-dimensional Riemannian manifold, let $\pi : U M \rightarrow M$ be the unit tangent bundle of $M$, let $d u$ be the Liouville measure on $UM$, and let $g _ { t } : U M \rightarrow U M$ be the geodesic flow. One way to define $d u$ is to start with the standard contact form $\alpha$ (cf. [[Contact structure|Contact structure]]) and define $d u = \alpha \wedge d \alpha ^ { n - 1 }$. Liouville's theorem says that $d u$ is invariant under the geodesic flow $g_{ t }$ (since $\alpha$ is). Locally, $d u$ is just the product measure $dm \times dv$ where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130020/s13002016.png"/> is the Riemannian volume form and $d v$ is the standard volume form on the unit $( n - 1 )$-sphere. |
| − | For any (locally defined) codimension-one submanifold | + | For any (locally defined) codimension-one submanifold $N \subset M$, let $d x$ be the Riemannian volume element of the submanifold. Let $S N = \pi ^ { - 1 } ( N ) \subset U M$, and, for each $x \in N$, let $N_x$ be a unit normal to $N$ at $x$. Then there is a smooth mapping $G : S N \times R \rightarrow U M$, given by $G ( v , t ) = g _ { t } ( v )$. Santaló's formula says: |
| − | + | \begin{equation*} G ^ { * } ( d u ) = | \langle v , N _ { x } \rangle | d t d v d x. \end{equation*} | |
| − | The formula is used to convert integrals over subsets | + | The formula is used to convert integrals over subsets $Q \subset U M$ of the unit tangent bundle to iterated integrals, first over a fixed unit-speed geodesic (say parametrized on $I ( \gamma ) \subset R$) and then over the space $\Gamma$ of geodesics which are parametrized by their intersections with a fixed codimension-one submanifold and endowed with the measure $d \gamma = | \langle v , N _ { x } \rangle | d v d x$, i.e. |
| − | + | \begin{equation*} \int _ { Q } f ( u ) d u = \int _ { \gamma \in \Gamma} \int_{ I ( \gamma ) } f ( \gamma ^ { \prime } ( t ) ) d t d \gamma. \end{equation*} | |
| − | One of the most important applications is to the study of Riemannian manifolds with smooth boundary. In this case | + | One of the most important applications is to the study of Riemannian manifolds with smooth boundary. In this case $N = \partial M$, $N_x$ is the inwardly pointing unit normal vector and $U ^ { + } \partial M = \{ v \in S N : \langle v , N _ { x } \rangle > 0 \}$. For any $u \in U M$, set $l ( u ) = \operatorname { sup } \{ t \geq 0 : g_t ( u ) \text { is defined} \}$. Note that $l ( u ) = \infty$ means that $g _ { t } ( u )$ is defined for all $t > 0$. Let $\overline { U M } = \{ u \in U M : l ( - u ) < \infty \} \cup U ^ { + } \partial M$, i.e. $u \in \overline { UM }$ means $u = g _ { t } ( v )$ for some some $v \in U ^ { + } \partial M$ and some $t \geq 0$. In this setting, Santaló's formula takes the form: |
| − | + | \begin{equation*} \int _ { \overline{U M} } f ( u ) d u = \int _ { U ^ { + } \partial M } \int _ { 0 } ^ { l ( v ) } f ( g _ { t } ( v ) ) d t \langle v , N _ { x } \rangle d v d x. \end{equation*} | |
| − | One immediate application, by simply putting | + | One immediate application, by simply putting $f ( u ) = 1$, is: |
| − | + | \begin{equation*} \operatorname { Vol } ( \overline { U M } ) = C _ { 1 } ( n ) \int _ { U ^ { + } \partial M } l ( v ) \langle v , N _ { x } \rangle d v d x. \end{equation*} | |
| − | Since the Liouville measure is locally a product measure, in the special case | + | Since the Liouville measure is locally a product measure, in the special case $\overline { UM } = UM$ this says <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130020/s13002051.png"/>. |
The formula is often used to prove isoperimetric and rigidity results. A sample of such applications can be found in the references. See [[#References|[a1]]] for Santaló's formula for time-like geodesic flow on Lorentzian surfaces. | The formula is often used to prove isoperimetric and rigidity results. A sample of such applications can be found in the references. See [[#References|[a1]]] for Santaló's formula for time-like geodesic flow on Lorentzian surfaces. | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> L. Andersson, M. Dahl, R. Howard, "Boundary and lens rigidity of Lorentzian surfaces" ''Trans. Amer. Math. Soc.'' , '''348''' : 6 (1996) pp. 2307–2329</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> C. Croke, "A sharp four-dimensional isoperimetric inequality" ''Comment. Math. Helv.'' , '''59''' : 2 (1984) pp. 187–192</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> C. Croke, "Some isoperimetric inequalities and eigenvalue estimates" ''Ann. Sci. École Norm. Sup.'' , '''13''' : 4 (1980) pp. 419–435</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> C. Croke, N. Dairbekov, V. Sharafutdinov, "Local boundary rigidity of a compact Riemannian manifold with curvature bounded above" ''Trans. Amer. Math. Soc.'' (to appear)</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> L.A. Santaló, "Measure of sets of geodesics in a Riemannian space and applications to integral formulas in elliptic and hyperbolic spaces" ''Summa Brasil. Math.'' , '''3''' (1952) pp. 1–11</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> L.A. Santaló, "Integral geometry and geometric probability (With a foreword by Mark Kac)" , ''Encyclopedia Math. Appl.'' , '''1''' , Addison-Wesley (1976)</td></tr></table> |
Revision as of 17:03, 1 July 2020
A formula describing the Liouville measure on the unit tangent bundle of a Riemannian manifold in terms of the geodesic flow and the measure of a codimension-one submanifold (see [a5] and [a6], Chap. 19).
Let $M$ be an $n$-dimensional Riemannian manifold, let $\pi : U M \rightarrow M$ be the unit tangent bundle of $M$, let $d u$ be the Liouville measure on $UM$, and let $g _ { t } : U M \rightarrow U M$ be the geodesic flow. One way to define $d u$ is to start with the standard contact form $\alpha$ (cf. Contact structure) and define $d u = \alpha \wedge d \alpha ^ { n - 1 }$. Liouville's theorem says that $d u$ is invariant under the geodesic flow $g_{ t }$ (since $\alpha$ is). Locally, $d u$ is just the product measure $dm \times dv$ where 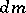 is the Riemannian volume form and $d v$ is the standard volume form on the unit $( n - 1 )$-sphere.
is the Riemannian volume form and $d v$ is the standard volume form on the unit $( n - 1 )$-sphere.
For any (locally defined) codimension-one submanifold $N \subset M$, let $d x$ be the Riemannian volume element of the submanifold. Let $S N = \pi ^ { - 1 } ( N ) \subset U M$, and, for each $x \in N$, let $N_x$ be a unit normal to $N$ at $x$. Then there is a smooth mapping $G : S N \times R \rightarrow U M$, given by $G ( v , t ) = g _ { t } ( v )$. Santaló's formula says:
\begin{equation*} G ^ { * } ( d u ) = | \langle v , N _ { x } \rangle | d t d v d x. \end{equation*}
The formula is used to convert integrals over subsets $Q \subset U M$ of the unit tangent bundle to iterated integrals, first over a fixed unit-speed geodesic (say parametrized on $I ( \gamma ) \subset R$) and then over the space $\Gamma$ of geodesics which are parametrized by their intersections with a fixed codimension-one submanifold and endowed with the measure $d \gamma = | \langle v , N _ { x } \rangle | d v d x$, i.e.
\begin{equation*} \int _ { Q } f ( u ) d u = \int _ { \gamma \in \Gamma} \int_{ I ( \gamma ) } f ( \gamma ^ { \prime } ( t ) ) d t d \gamma. \end{equation*}
One of the most important applications is to the study of Riemannian manifolds with smooth boundary. In this case $N = \partial M$, $N_x$ is the inwardly pointing unit normal vector and $U ^ { + } \partial M = \{ v \in S N : \langle v , N _ { x } \rangle > 0 \}$. For any $u \in U M$, set $l ( u ) = \operatorname { sup } \{ t \geq 0 : g_t ( u ) \text { is defined} \}$. Note that $l ( u ) = \infty$ means that $g _ { t } ( u )$ is defined for all $t > 0$. Let $\overline { U M } = \{ u \in U M : l ( - u ) < \infty \} \cup U ^ { + } \partial M$, i.e. $u \in \overline { UM }$ means $u = g _ { t } ( v )$ for some some $v \in U ^ { + } \partial M$ and some $t \geq 0$. In this setting, Santaló's formula takes the form:
\begin{equation*} \int _ { \overline{U M} } f ( u ) d u = \int _ { U ^ { + } \partial M } \int _ { 0 } ^ { l ( v ) } f ( g _ { t } ( v ) ) d t \langle v , N _ { x } \rangle d v d x. \end{equation*}
One immediate application, by simply putting $f ( u ) = 1$, is:
\begin{equation*} \operatorname { Vol } ( \overline { U M } ) = C _ { 1 } ( n ) \int _ { U ^ { + } \partial M } l ( v ) \langle v , N _ { x } \rangle d v d x. \end{equation*}
Since the Liouville measure is locally a product measure, in the special case $\overline { UM } = UM$ this says 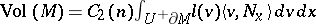 .
.
The formula is often used to prove isoperimetric and rigidity results. A sample of such applications can be found in the references. See [a1] for Santaló's formula for time-like geodesic flow on Lorentzian surfaces.
References
| [a1] | L. Andersson, M. Dahl, R. Howard, "Boundary and lens rigidity of Lorentzian surfaces" Trans. Amer. Math. Soc. , 348 : 6 (1996) pp. 2307–2329 |
| [a2] | C. Croke, "A sharp four-dimensional isoperimetric inequality" Comment. Math. Helv. , 59 : 2 (1984) pp. 187–192 |
| [a3] | C. Croke, "Some isoperimetric inequalities and eigenvalue estimates" Ann. Sci. École Norm. Sup. , 13 : 4 (1980) pp. 419–435 |
| [a4] | C. Croke, N. Dairbekov, V. Sharafutdinov, "Local boundary rigidity of a compact Riemannian manifold with curvature bounded above" Trans. Amer. Math. Soc. (to appear) |
| [a5] | L.A. Santaló, "Measure of sets of geodesics in a Riemannian space and applications to integral formulas in elliptic and hyperbolic spaces" Summa Brasil. Math. , 3 (1952) pp. 1–11 |
| [a6] | L.A. Santaló, "Integral geometry and geometric probability (With a foreword by Mark Kac)" , Encyclopedia Math. Appl. , 1 , Addison-Wesley (1976) |
Santaló formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Santal%C3%B3_formula&oldid=23516