Difference between revisions of "Szegö limit theorems"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
m (AUTOMATIC EDIT (latexlist): Replaced 73 formulas out of 75 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 75 formulas, 73 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|partial}} | |
| + | Let $a$ be a complex-valued function defined on the complex unit circle $\bf T$, with [[Fourier coefficients|Fourier coefficients]] | ||
| − | + | \begin{equation*} a _ { n } = \frac { 1 } { 2 \pi } \int _ { 0 } ^ { 2 \pi } a ( e ^ { i \theta } ) e ^ { - i n \theta } d \theta. \end{equation*} | |
| − | + | Szegö limit theorems describe the behaviour of the determinants of the Toeplitz matrices $T _ { n } ( a ) = ( a _ { j - k } ) _ { j , k = 0 } ^ { n - 1 }$, as $n$ tends to infinity, for certain classes of functions $a$ (cf. also [[Toeplitz matrix|Toeplitz matrix]]). | |
| − | with the constant | + | For real positive functions $a \in L ^ { 1 } ( {\bf T} )$ for which $\operatorname { log } a \in L ^ { 1 } (\bf T )$, G. Szegö [[#References|[a7]]] has proved that |
| + | |||
| + | \begin{equation} \tag{a1} \operatorname { lim } _ { n \rightarrow \infty } \frac { \operatorname { det } T _ { n } ( a ) } { \operatorname { det } T _ { n - 1 } ( a ) } = G ( a ), \end{equation} | ||
| + | |||
| + | with the constant $G ( a ) = \operatorname { exp } ( [ \operatorname { log } a ] _ { 0 } )$. Here, $[ \operatorname { log } a ] _ { k }$ stands for the $k$th Fourier coefficient of the logarithm of $a$. A statement of type (a1) is referred to as a first Szegö limit theorem. Szegö's result has been considerably extended. In particular, (a1) holds for functions that are the exponentials of continuous complex-valued functions defined on the unit circle. | ||
The strong Szegö limit theorem states that | The strong Szegö limit theorem states that | ||
| − | + | \begin{equation} \tag{a2} \operatorname { lim } _ { n \rightarrow \infty } \frac { \operatorname { det } T _ { n } ( a ) } { G ( a ) ^ { N } } = E ( a ), \end{equation} | |
| − | with the constant | + | with the constant $E ( a )$ defined by |
| − | + | \begin{equation*} E ( a ) = \operatorname { exp } \left( \sum _ { k = 1 } ^ { \infty } k [ \operatorname { log } a ] _ { k } [ \operatorname { log } a ]_{ - k} \right). \end{equation*} | |
Relation (a2) was first proved by Szegö [[#References|[a8]]] for positive real functions whose derivatives satisfy a Hölder–Lipschitz condition. This result has been generalized too. For instance, the strong Szegö limit theorem holds for functions that are the exponentials of continuous and sufficiently smooth complex-valued functions defined on the unit circle. | Relation (a2) was first proved by Szegö [[#References|[a8]]] for positive real functions whose derivatives satisfy a Hölder–Lipschitz condition. This result has been generalized too. For instance, the strong Szegö limit theorem holds for functions that are the exponentials of continuous and sufficiently smooth complex-valued functions defined on the unit circle. | ||
| − | Such results about the asymptotics of Toeplitz determinants can be used to obtain information about the asymptotic distribution of the eigenvalues | + | Such results about the asymptotics of Toeplitz determinants can be used to obtain information about the asymptotic distribution of the eigenvalues $\{ \lambda _ { k } ^ { ( n ) } \} _ { k = 1 } ^ { n }$ of the matrices $T _ { n } ( a )$. It turns out that |
| − | + | \begin{equation} \tag{a3} \frac { 1 } { n } \sum _ { k = 1 } ^ { n } f ( \lambda _ { k } ^ { ( n ) } ) = \frac { 1 } { 2 \pi } \int _ { 0 } ^ { 2 \pi } f ( a ( e ^ { i \theta } ) ) d \theta + o ( 1 ), \end{equation} | |
| − | as | + | as $n \rightarrow \infty$, if, for instance, one of the following assumptions is satisfied: |
| − | + | $a \in L ^ { 1 } ( {\bf T} )$ is real-valued and $f$ is a [[Continuous function|continuous function]] on the real line with a compact support [[#References|[a9]]]; | |
| − | + | $a$ is a continuous complex-valued function and $f$ is an [[Analytic function|analytic function]] defined on an open neighbourhood of the set | |
| − | + | \begin{equation*} \operatorname{spec} T ( a ) = \operatorname { Ran } ( a ) \bigcup \{ z \notin \operatorname { Ran } ( a ) : \text { wind } ( a - z ) \neq 0 \}. \end{equation*} | |
| − | Here, | + | Here, $T ( a ) = ( a _ { j - k} ) _ { j , k = 0} ^ { \infty }$ stands for the [[Toeplitz operator|Toeplitz operator]] acting on the [[Hilbert space|Hilbert space]] $\text{l} ^ { 2 }$, $\operatorname {spec} T ( a )$ refers to its spectrum (cf. also [[Spectrum of an operator|Spectrum of an operator]]), $\operatorname{Ran}( a )$ stands for the range of the function $a$, and $\operatorname{wind}( a - z )$ denotes the [[Winding number|winding number]] of the function $a ( e ^ { i \theta } ) - z$. The asymptotic formula (a3) is sometimes also called the first Szegö limit theorem or a first-order trace formula. A second-order trace formula, which is the pendant of the strong Szegö limit theorem, has also been established [[#References|[a2]]], [[#References|[a10]]]. |
| − | Some work was also done in order to determine the higher-order terms of the [[Asymptotic expansion|asymptotic expansion]] of Toeplitz determinants [[#References|[a1]]]. Exact formulas for Toeplitz determinants in terms of the Wiener–Hopf factorization (cf. also [[Wiener–Hopf method|Wiener–Hopf method]]; [[Wiener–Hopf operator|Wiener–Hopf operator]]) of the generating function | + | Some work was also done in order to determine the higher-order terms of the [[Asymptotic expansion|asymptotic expansion]] of Toeplitz determinants [[#References|[a1]]]. Exact formulas for Toeplitz determinants in terms of the Wiener–Hopf factorization (cf. also [[Wiener–Hopf method|Wiener–Hopf method]]; [[Wiener–Hopf operator|Wiener–Hopf operator]]) of the generating function $a$ do also exist (see, e.g., [[#References|[a11]]]). |
| − | H. Widom [[#References|[a10]]] was the first to give a crystal clear proof of the strong Szegö limit theorem, by an elegant application of ideas from operator theory and thereby replacing earlier long-winded proofs. With his approach he was able to generalize this theorem to the case of matrix-valued functions. Under the assumption that | + | H. Widom [[#References|[a10]]] was the first to give a crystal clear proof of the strong Szegö limit theorem, by an elegant application of ideas from operator theory and thereby replacing earlier long-winded proofs. With his approach he was able to generalize this theorem to the case of matrix-valued functions. Under the assumption that $a$ is a sufficiently smooth matrix-valued function defined on the unit circle for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130640/s13064035.png"/> is the exponential of a continuous function, (a2) still holds, but with constants defined by $G ( a ) = \operatorname { exp } ( [ \operatorname { log } \operatorname { det } a ] _ { 0 } )$ and $E ( a ) = \operatorname { det } T ( a ) T ( a ^ { - 1 } )$. The last expression has to be understood as an operator determinant. In this connection, the identity <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130640/s13064038.png"/> plays an important role, where $H ( a ) = ( a _ { 1 + j + k} )_{ j,k = 0}^{\infty}$ is a [[Hankel operator|Hankel operator]] and $\tilde { a } ( e ^ { i \theta } ) = a ( e ^ { - i \theta } )$. Note that for sufficiently smooth and invertible matrix functions $a$ the operator $H ( a ) H ( \tilde{a} ^ { - 1 } )$ is a trace-class operator (cf. also [[Nuclear operator|Nuclear operator]]). An explicit expression for $E ( a )$ is not known yet (as of 2000), apart from special cases related to the scalar situation. On the other hand, an operator-valued version of the strong Szegö limit theorem has been established [[#References|[a3]]]. |
| − | The asymptotic behaviour of Toeplitz determinants changes considerably if the function | + | The asymptotic behaviour of Toeplitz determinants changes considerably if the function $a$ is discontinuous. If $a$ possesses zeros, poles, jumps, or certain oscillations, then the asymptotics is predicted by the Fisher–Hartwig conjecture or by the more general Basor–Tracy conjecture. Let |
| − | + | \begin{equation*} a ( e ^ { i \theta } ) = b ( e ^ { i \theta } ) \prod _ { r = 1 } ^ { R } \omega _ { \alpha _ { r } , \beta _ { r } } ( e ^ { i ( \theta - \theta _ { r } ) } ), \end{equation*} | |
| − | where | + | where $\theta _ { 1 } , \dots , \theta _ { R } \in [ 0,2 \pi )$ are distinct points, $b$ is the exponential of a sufficiently smooth function and $\alpha_r$, $\beta _ { r }$ are complex parameters. The function $\omega _ { \alpha , \beta }$ is defined as |
| − | + | \begin{equation*} \omega _ { \alpha , \beta } ( e ^ { i \theta } ) = ( 2 - 2 \operatorname { cos } \theta ) ^ { \alpha } e ^ { i \beta ( \theta - \pi ) } , 0 < \theta < 2 \pi . \end{equation*} | |
Then the Fisher–Hartwig conjecture [[#References|[a6]]] asserts that | Then the Fisher–Hartwig conjecture [[#References|[a6]]] asserts that | ||
| − | + | \begin{equation*} \operatorname { lim } _ { n \rightarrow \infty } \frac { \operatorname { det } T _ { n } ( a ) } { G ( b ) ^ { n } n ^ { \Omega } } = E, \end{equation*} | |
| − | where | + | where $\Omega = \sum _ { r = 1 } ^ { R } ( \alpha _ { r } ^ { 2 } - \beta _ { r } ^ { 2 } )$. An explicit, but more complicated expression is known for the constant $E$. It has turned out that in some cases the Fisher–Hartwig conjecture breaks down. However, this conjecture has been proved in all the cases in which it is suspected to apply [[#References|[a2]]], [[#References|[a5]]]. It is believed that the Basor–Tracy conjecture [[#References|[a4]]], which is proved so far (2000) only in special cases, gives the correct answer for all cases. |
| − | The continuous analogue of Toeplitz determinants are the determinants of truncated Wiener–Hopf operators (cf. also [[Wiener–Hopf operator|Wiener–Hopf operator]]). Let | + | The continuous analogue of Toeplitz determinants are the determinants of truncated Wiener–Hopf operators (cf. also [[Wiener–Hopf operator|Wiener–Hopf operator]]). Let $k$ be a complex-valued function in $L ^ { 1 } ( \mathbf{R} ) \cap L ^ { \infty } ( \mathbf{R} )$ defined on the real axis, and denote by $\hat{k}$ the [[Fourier transform|Fourier transform]] of $k$. The [[Integral operator|integral operator]] defined on $L ^ { 2 } [ 0 , \tau ]$ with kernel $\hat { k } ( x - y )$ is called a truncated Wiener–Hopf operator and denoted by $W _ { \tau } ( k )$. Under the above assumption, $W _ { \tau } ( k )$ is a trace-class operator. The asymptotics of the operator determinants of $I + W _ { \tau } ( k )$, as $\tau \rightarrow \infty$, for certain classes of functions $k$ is described by the Akhiezer–Kac formula, which is the continuous pendant of the strong Szegö limit theorem. Suppose $a = 1 + k = \operatorname { exp } ( s )$, where $s \in L ^ { 1 } ( \mathbf{R} ) \cap L ^ { \infty } ( \mathbf{R} )$ such that its Fourier transform $\stackrel \frown {s} $ belongs to $L ^ { 1 } ( \mathbf{R} )$ and |
| − | + | \begin{equation*} \int _ { - \infty } ^ { \infty } | t | | \hat{s} ( t ) | ^ { 2 } d t < \infty. \end{equation*} | |
Then | Then | ||
| − | + | \begin{equation*} \operatorname { lim } _ { \tau \rightarrow \infty } \frac { \operatorname { det } ( I + W _ { \tau } ( k ) ) } { G ( a ) ^ { \tau } } = E ( a ), \end{equation*} | |
| − | with the constants | + | with the constants $G ( a ) = \operatorname { exp } ( \hat{s} ( 0 ) )$ and |
| − | + | \begin{equation*} E ( a ) = \operatorname { exp } \left( \int _ { 0 } ^ { \infty } t \hat{s} ( t ) \hat{s} ( - t ) d t \right) . \end{equation*} | |
There are many further results for Wiener–Hopf determinants which are quite similar to those of the discrete case [[#References|[a1]]], [[#References|[a2]]]. | There are many further results for Wiener–Hopf determinants which are quite similar to those of the discrete case [[#References|[a1]]], [[#References|[a2]]]. | ||
| Line 69: | Line 77: | ||
Finally, analogues of the Szegö limit theorem have also been established for multi-dimensional (i.e., multi-level) Toeplitz and Wiener–Hopf operators, for pseudo-differential operators, and in several abstract settings. | Finally, analogues of the Szegö limit theorem have also been established for multi-dimensional (i.e., multi-level) Toeplitz and Wiener–Hopf operators, for pseudo-differential operators, and in several abstract settings. | ||
| − | Another direction deals with the asymptotic distribution of the singular values of the matrices | + | Another direction deals with the asymptotic distribution of the singular values of the matrices $T _ { n } ( a )$, their analogues and generalizations. Results of such a type are called Avram–Parter theorems [[#References|[a2]]]. |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> A. Böttcher, B. Silbermann, "Analysis of Toeplitz operators" , Springer (1990) {{MR|1086453}} {{MR|1071374}} {{ZBL|0732.47029}} </td></tr><tr><td valign="top">[a2]</td> <td valign="top"> A. Böttcher, B. Silbermann, "Introduction to large truncated Toeplitz matrices" , Springer (1998)</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> A. Böttcher, B. Silbermann, "Operator-valued Szegö-Widom limit theorems" , ''Oper. Theory Adv. Appl.'' , '''71''' , Birkhäuser (1994) pp. 33–53</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> E.L. Basor, C.A. Tracy, "The Fisher–Hartwig conjecture and generalizations" ''Phys. A'' , '''177''' (1991) pp. 167–173</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> T. Ehrhardt, "Toeplitz determinants with several Fisher–Hartwig singularities" ''PhD Thesis Techn. Univ. Chemnitz'' (1997)</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> M.E. Fisher, R.E. Hartwig, "Toeplitz determinants: Some applications, theorems and conjectures" ''Adv. Chem. Phys.'' , '''15''' (1968) pp. 333–353</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> G. Szegö, "Ein Grenzwertsatz über die Toeplitzschen Determinanten einer reellen positiven Funktion" ''Math. Ann.'' , '''76''' (1915) pp. 490–503</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> G. Szegö, "On certain Hermitian forms associated with the Fourier series of a positive function" ''Comm. Sém. Math. Univ. Lund'' (1952) pp. 228–238</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> N.L. Zamarashkin, E.E. Tyrtyshnikov, "Distribution of eigenvalues and singular numbers of Toeplitz matrices under weakened requirements of the generating function" ''Mat. Sb.'' , '''188''' (1997) pp. 83–92 (In Russian)</td></tr><tr><td valign="top">[a10]</td> <td valign="top"> H. Widom, "Asymptotic behavior of block Toeplitz matrices and determinants. II" ''Adv. Math.'' , '''21''' (1976) pp. 1–29</td></tr><tr><td valign="top">[a11]</td> <td valign="top"> E.L. Basor, H. Widom, "On a Toeplitz determinant identity of Borodin and Okounov" ''Integral Eq. Oper. Th.'' , '''37''' : 4 (2000) pp. 397–401</td></tr></table> |
Revision as of 16:58, 1 July 2020
Let $a$ be a complex-valued function defined on the complex unit circle $\bf T$, with Fourier coefficients
\begin{equation*} a _ { n } = \frac { 1 } { 2 \pi } \int _ { 0 } ^ { 2 \pi } a ( e ^ { i \theta } ) e ^ { - i n \theta } d \theta. \end{equation*}
Szegö limit theorems describe the behaviour of the determinants of the Toeplitz matrices $T _ { n } ( a ) = ( a _ { j - k } ) _ { j , k = 0 } ^ { n - 1 }$, as $n$ tends to infinity, for certain classes of functions $a$ (cf. also Toeplitz matrix).
For real positive functions $a \in L ^ { 1 } ( {\bf T} )$ for which $\operatorname { log } a \in L ^ { 1 } (\bf T )$, G. Szegö [a7] has proved that
\begin{equation} \tag{a1} \operatorname { lim } _ { n \rightarrow \infty } \frac { \operatorname { det } T _ { n } ( a ) } { \operatorname { det } T _ { n - 1 } ( a ) } = G ( a ), \end{equation}
with the constant $G ( a ) = \operatorname { exp } ( [ \operatorname { log } a ] _ { 0 } )$. Here, $[ \operatorname { log } a ] _ { k }$ stands for the $k$th Fourier coefficient of the logarithm of $a$. A statement of type (a1) is referred to as a first Szegö limit theorem. Szegö's result has been considerably extended. In particular, (a1) holds for functions that are the exponentials of continuous complex-valued functions defined on the unit circle.
The strong Szegö limit theorem states that
\begin{equation} \tag{a2} \operatorname { lim } _ { n \rightarrow \infty } \frac { \operatorname { det } T _ { n } ( a ) } { G ( a ) ^ { N } } = E ( a ), \end{equation}
with the constant $E ( a )$ defined by
\begin{equation*} E ( a ) = \operatorname { exp } \left( \sum _ { k = 1 } ^ { \infty } k [ \operatorname { log } a ] _ { k } [ \operatorname { log } a ]_{ - k} \right). \end{equation*}
Relation (a2) was first proved by Szegö [a8] for positive real functions whose derivatives satisfy a Hölder–Lipschitz condition. This result has been generalized too. For instance, the strong Szegö limit theorem holds for functions that are the exponentials of continuous and sufficiently smooth complex-valued functions defined on the unit circle.
Such results about the asymptotics of Toeplitz determinants can be used to obtain information about the asymptotic distribution of the eigenvalues $\{ \lambda _ { k } ^ { ( n ) } \} _ { k = 1 } ^ { n }$ of the matrices $T _ { n } ( a )$. It turns out that
\begin{equation} \tag{a3} \frac { 1 } { n } \sum _ { k = 1 } ^ { n } f ( \lambda _ { k } ^ { ( n ) } ) = \frac { 1 } { 2 \pi } \int _ { 0 } ^ { 2 \pi } f ( a ( e ^ { i \theta } ) ) d \theta + o ( 1 ), \end{equation}
as $n \rightarrow \infty$, if, for instance, one of the following assumptions is satisfied:
$a \in L ^ { 1 } ( {\bf T} )$ is real-valued and $f$ is a continuous function on the real line with a compact support [a9];
$a$ is a continuous complex-valued function and $f$ is an analytic function defined on an open neighbourhood of the set
\begin{equation*} \operatorname{spec} T ( a ) = \operatorname { Ran } ( a ) \bigcup \{ z \notin \operatorname { Ran } ( a ) : \text { wind } ( a - z ) \neq 0 \}. \end{equation*}
Here, $T ( a ) = ( a _ { j - k} ) _ { j , k = 0} ^ { \infty }$ stands for the Toeplitz operator acting on the Hilbert space $\text{l} ^ { 2 }$, $\operatorname {spec} T ( a )$ refers to its spectrum (cf. also Spectrum of an operator), $\operatorname{Ran}( a )$ stands for the range of the function $a$, and $\operatorname{wind}( a - z )$ denotes the winding number of the function $a ( e ^ { i \theta } ) - z$. The asymptotic formula (a3) is sometimes also called the first Szegö limit theorem or a first-order trace formula. A second-order trace formula, which is the pendant of the strong Szegö limit theorem, has also been established [a2], [a10].
Some work was also done in order to determine the higher-order terms of the asymptotic expansion of Toeplitz determinants [a1]. Exact formulas for Toeplitz determinants in terms of the Wiener–Hopf factorization (cf. also Wiener–Hopf method; Wiener–Hopf operator) of the generating function $a$ do also exist (see, e.g., [a11]).
H. Widom [a10] was the first to give a crystal clear proof of the strong Szegö limit theorem, by an elegant application of ideas from operator theory and thereby replacing earlier long-winded proofs. With his approach he was able to generalize this theorem to the case of matrix-valued functions. Under the assumption that $a$ is a sufficiently smooth matrix-valued function defined on the unit circle for which 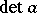 is the exponential of a continuous function, (a2) still holds, but with constants defined by $G ( a ) = \operatorname { exp } ( [ \operatorname { log } \operatorname { det } a ] _ { 0 } )$ and $E ( a ) = \operatorname { det } T ( a ) T ( a ^ { - 1 } )$. The last expression has to be understood as an operator determinant. In this connection, the identity
is the exponential of a continuous function, (a2) still holds, but with constants defined by $G ( a ) = \operatorname { exp } ( [ \operatorname { log } \operatorname { det } a ] _ { 0 } )$ and $E ( a ) = \operatorname { det } T ( a ) T ( a ^ { - 1 } )$. The last expression has to be understood as an operator determinant. In this connection, the identity 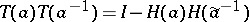 plays an important role, where $H ( a ) = ( a _ { 1 + j + k} )_{ j,k = 0}^{\infty}$ is a Hankel operator and $\tilde { a } ( e ^ { i \theta } ) = a ( e ^ { - i \theta } )$. Note that for sufficiently smooth and invertible matrix functions $a$ the operator $H ( a ) H ( \tilde{a} ^ { - 1 } )$ is a trace-class operator (cf. also Nuclear operator). An explicit expression for $E ( a )$ is not known yet (as of 2000), apart from special cases related to the scalar situation. On the other hand, an operator-valued version of the strong Szegö limit theorem has been established [a3].
plays an important role, where $H ( a ) = ( a _ { 1 + j + k} )_{ j,k = 0}^{\infty}$ is a Hankel operator and $\tilde { a } ( e ^ { i \theta } ) = a ( e ^ { - i \theta } )$. Note that for sufficiently smooth and invertible matrix functions $a$ the operator $H ( a ) H ( \tilde{a} ^ { - 1 } )$ is a trace-class operator (cf. also Nuclear operator). An explicit expression for $E ( a )$ is not known yet (as of 2000), apart from special cases related to the scalar situation. On the other hand, an operator-valued version of the strong Szegö limit theorem has been established [a3].
The asymptotic behaviour of Toeplitz determinants changes considerably if the function $a$ is discontinuous. If $a$ possesses zeros, poles, jumps, or certain oscillations, then the asymptotics is predicted by the Fisher–Hartwig conjecture or by the more general Basor–Tracy conjecture. Let
\begin{equation*} a ( e ^ { i \theta } ) = b ( e ^ { i \theta } ) \prod _ { r = 1 } ^ { R } \omega _ { \alpha _ { r } , \beta _ { r } } ( e ^ { i ( \theta - \theta _ { r } ) } ), \end{equation*}
where $\theta _ { 1 } , \dots , \theta _ { R } \in [ 0,2 \pi )$ are distinct points, $b$ is the exponential of a sufficiently smooth function and $\alpha_r$, $\beta _ { r }$ are complex parameters. The function $\omega _ { \alpha , \beta }$ is defined as
\begin{equation*} \omega _ { \alpha , \beta } ( e ^ { i \theta } ) = ( 2 - 2 \operatorname { cos } \theta ) ^ { \alpha } e ^ { i \beta ( \theta - \pi ) } , 0 < \theta < 2 \pi . \end{equation*}
Then the Fisher–Hartwig conjecture [a6] asserts that
\begin{equation*} \operatorname { lim } _ { n \rightarrow \infty } \frac { \operatorname { det } T _ { n } ( a ) } { G ( b ) ^ { n } n ^ { \Omega } } = E, \end{equation*}
where $\Omega = \sum _ { r = 1 } ^ { R } ( \alpha _ { r } ^ { 2 } - \beta _ { r } ^ { 2 } )$. An explicit, but more complicated expression is known for the constant $E$. It has turned out that in some cases the Fisher–Hartwig conjecture breaks down. However, this conjecture has been proved in all the cases in which it is suspected to apply [a2], [a5]. It is believed that the Basor–Tracy conjecture [a4], which is proved so far (2000) only in special cases, gives the correct answer for all cases.
The continuous analogue of Toeplitz determinants are the determinants of truncated Wiener–Hopf operators (cf. also Wiener–Hopf operator). Let $k$ be a complex-valued function in $L ^ { 1 } ( \mathbf{R} ) \cap L ^ { \infty } ( \mathbf{R} )$ defined on the real axis, and denote by $\hat{k}$ the Fourier transform of $k$. The integral operator defined on $L ^ { 2 } [ 0 , \tau ]$ with kernel $\hat { k } ( x - y )$ is called a truncated Wiener–Hopf operator and denoted by $W _ { \tau } ( k )$. Under the above assumption, $W _ { \tau } ( k )$ is a trace-class operator. The asymptotics of the operator determinants of $I + W _ { \tau } ( k )$, as $\tau \rightarrow \infty$, for certain classes of functions $k$ is described by the Akhiezer–Kac formula, which is the continuous pendant of the strong Szegö limit theorem. Suppose $a = 1 + k = \operatorname { exp } ( s )$, where $s \in L ^ { 1 } ( \mathbf{R} ) \cap L ^ { \infty } ( \mathbf{R} )$ such that its Fourier transform $\stackrel \frown {s} $ belongs to $L ^ { 1 } ( \mathbf{R} )$ and
\begin{equation*} \int _ { - \infty } ^ { \infty } | t | | \hat{s} ( t ) | ^ { 2 } d t < \infty. \end{equation*}
Then
\begin{equation*} \operatorname { lim } _ { \tau \rightarrow \infty } \frac { \operatorname { det } ( I + W _ { \tau } ( k ) ) } { G ( a ) ^ { \tau } } = E ( a ), \end{equation*}
with the constants $G ( a ) = \operatorname { exp } ( \hat{s} ( 0 ) )$ and
\begin{equation*} E ( a ) = \operatorname { exp } \left( \int _ { 0 } ^ { \infty } t \hat{s} ( t ) \hat{s} ( - t ) d t \right) . \end{equation*}
There are many further results for Wiener–Hopf determinants which are quite similar to those of the discrete case [a1], [a2].
Finally, analogues of the Szegö limit theorem have also been established for multi-dimensional (i.e., multi-level) Toeplitz and Wiener–Hopf operators, for pseudo-differential operators, and in several abstract settings.
Another direction deals with the asymptotic distribution of the singular values of the matrices $T _ { n } ( a )$, their analogues and generalizations. Results of such a type are called Avram–Parter theorems [a2].
References
| [a1] | A. Böttcher, B. Silbermann, "Analysis of Toeplitz operators" , Springer (1990) MR1086453 MR1071374 Zbl 0732.47029 |
| [a2] | A. Böttcher, B. Silbermann, "Introduction to large truncated Toeplitz matrices" , Springer (1998) |
| [a3] | A. Böttcher, B. Silbermann, "Operator-valued Szegö-Widom limit theorems" , Oper. Theory Adv. Appl. , 71 , Birkhäuser (1994) pp. 33–53 |
| [a4] | E.L. Basor, C.A. Tracy, "The Fisher–Hartwig conjecture and generalizations" Phys. A , 177 (1991) pp. 167–173 |
| [a5] | T. Ehrhardt, "Toeplitz determinants with several Fisher–Hartwig singularities" PhD Thesis Techn. Univ. Chemnitz (1997) |
| [a6] | M.E. Fisher, R.E. Hartwig, "Toeplitz determinants: Some applications, theorems and conjectures" Adv. Chem. Phys. , 15 (1968) pp. 333–353 |
| [a7] | G. Szegö, "Ein Grenzwertsatz über die Toeplitzschen Determinanten einer reellen positiven Funktion" Math. Ann. , 76 (1915) pp. 490–503 |
| [a8] | G. Szegö, "On certain Hermitian forms associated with the Fourier series of a positive function" Comm. Sém. Math. Univ. Lund (1952) pp. 228–238 |
| [a9] | N.L. Zamarashkin, E.E. Tyrtyshnikov, "Distribution of eigenvalues and singular numbers of Toeplitz matrices under weakened requirements of the generating function" Mat. Sb. , 188 (1997) pp. 83–92 (In Russian) |
| [a10] | H. Widom, "Asymptotic behavior of block Toeplitz matrices and determinants. II" Adv. Math. , 21 (1976) pp. 1–29 |
| [a11] | E.L. Basor, H. Widom, "On a Toeplitz determinant identity of Borodin and Okounov" Integral Eq. Oper. Th. , 37 : 4 (2000) pp. 397–401 |
Szegö limit theorems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Szeg%C3%B6_limit_theorems&oldid=24575