Difference between revisions of "Eilenberg-Moore algebra"
From Encyclopedia of Mathematics
Ulf Rehmann (talk | contribs) m (moved Eilenberg–Moore algebra to Eilenberg-Moore algebra: ascii title) |
m (AUTOMATIC EDIT (latexlist): Replaced 10 formulas out of 12 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 12 formulas, 10 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|partial}} | ||
''Moore–Eilenberg algebra'' | ''Moore–Eilenberg algebra'' | ||
| − | Given a monad (or [[Triple|triple]]) | + | Given a monad (or [[Triple|triple]]) $T$ in a [[Category|category]] $\mathcal{C}$, a $T$-algebra is a pair $( A , \alpha )$, $\alpha : T A \rightarrow A$, $A \in \mathcal{C}$, such that the diagram |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e120/e120080/e1200808.png"/></td> </tr></table> |
| − | commutes. Such a | + | commutes. Such a $T$-algebra is also called an Eilenberg–Moore algebra. The forgetful functor from the category of Eilenberg–Moore algebras $\mathcal{C} ^ { T }$ to $\mathcal{C}$ has a left adjoint, exhibiting the monad $T$ as coming from a pair of adjoint functors (the Eilenberg–Moore construction). |
See also [[Adjoint functor|Adjoint functor]]. | See also [[Adjoint functor|Adjoint functor]]. | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> F. Borceux, "Handbook of categorical algebra: Categories and structures" , '''2''' , Cambridge Univ. Press (1994) pp. Chap. 4</td></tr></table> |
Revision as of 16:45, 1 July 2020
Moore–Eilenberg algebra
Given a monad (or triple) $T$ in a category $\mathcal{C}$, a $T$-algebra is a pair $( A , \alpha )$, $\alpha : T A \rightarrow A$, $A \in \mathcal{C}$, such that the diagram
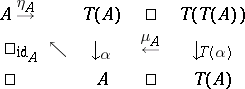 |
commutes. Such a $T$-algebra is also called an Eilenberg–Moore algebra. The forgetful functor from the category of Eilenberg–Moore algebras $\mathcal{C} ^ { T }$ to $\mathcal{C}$ has a left adjoint, exhibiting the monad $T$ as coming from a pair of adjoint functors (the Eilenberg–Moore construction).
See also Adjoint functor.
References
| [a1] | F. Borceux, "Handbook of categorical algebra: Categories and structures" , 2 , Cambridge Univ. Press (1994) pp. Chap. 4 |
How to Cite This Entry:
Eilenberg-Moore algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Eilenberg-Moore_algebra&oldid=22373
Eilenberg-Moore algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Eilenberg-Moore_algebra&oldid=22373
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article