Difference between revisions of "Steenrod-Sitnikov homology"
Ulf Rehmann (talk | contribs) m (moved Steenrod–Sitnikov homology to Steenrod-Sitnikov homology: ascii title) |
m (AUTOMATIC EDIT (latexlist): Replaced 56 formulas out of 57 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 57 formulas, 56 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|partial}} | |
| + | A [[Homology theory|homology theory]] $h_* ^ { S }$ supposed to be defined on the [[Category|category]] of pairs of compact metric (i.e., metrizable) spaces $\bf K$, satisfying all [[Steenrod–Eilenberg axioms|Steenrod–Eilenberg axioms]] (in the case of generalized Steenrod–Sitnikov homology, without a dimension axiom) together with a strong excision axiom (i.e. $p : ( X , A ) \rightarrow ( X / A , * )$ induces an isomorphism in homology). | ||
| − | + | For an ordinary Steenrod–Sitnikov homology theory $H _ { * } ^ { S } (\cdot \ ; G )$ ($G$ an Abelian group) J. Milnor [[#References|[a3]]] established the following axiomatic characterization: An ordinary homology theory $H _ * (\, . \, ; G )$ on $\bf K$ satisfying the Eilenberg–Steenrod axioms (with strong excision and dimension axiom) and in addition the cluster (or strong wedge) axiom is isomorphic (as a homology theory) to $H _ { * } ^ { S } (\cdot \ ; G )$. | |
| + | |||
| + | Let $( X _ { i } , x _ { i 0 } ) = X_i$, $i = 1,2 , \dots$, be a family of based spaces in $\bf K$; then the cluster $\operatorname {Cl} _ { i = 1 } ^ { \infty } ( X _ { i } , x _ { i_0 } ) = ( X , x _ { 0 } )$ is the wedge of the $X_i$, equipped with the [[Strong topology|strong topology]] (a neighbourhood of the basepoint $x _ { 0 }$ contains almost all $X_i$ or, alternatively, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120240/s12024016.png"/>). The projection $p _ { i } : X \rightarrow X_i$ induces a mapping | ||
| + | |||
| + | \begin{equation} \tag{a1} H_{*} ( X , x _ { 0 } ; G ) \overset{\approx}{\rightarrow} \prod _ { 1 } ^ { \infty } H_{*} ( X _ { i } , x _ { i 0 } ; G ). \end{equation} | ||
The cluster axiom requires that (a1) be an isomorphism. | The cluster axiom requires that (a1) be an isomorphism. | ||
| − | The cluster axiom turns out to be some kind of continuity axiom: A homology theory | + | The cluster axiom turns out to be some kind of continuity axiom: A homology theory $h_* $ is continuous whenever there is a natural isomorphism |
| − | + | \begin{equation} \tag{a2} \operatorname{varprojlim}_kh * ( X _ { k } ) = h * ( \text { varprojlim } _ { k } X _ { k } ), \end{equation} | |
| − | i.e. the functor | + | i.e. the functor $h_* $ commutes with inverse limits. S. Eilenberg and N. Steenrod [[#References|[a2]]] discovered that there is a conflict between (a2) and the exactness axiom, so that no homology theory can be continuous. However, the cluster axiom reveals itself as a special case of (a2): One has |
| − | + | \begin{equation*} \operatorname{varprojlim}_{k}( X _ { 1 } \vee \ldots \vee X _ { k } ) = \operatorname{Cl} _ { i = 1 } ^ { \infty } ( X _ { i } , x _ { i 0 } ). \end{equation*} | |
and | and | ||
| − | + | \begin{equation*} \operatorname { varprojlim}_{k} h_{ *} ( X _ { 1 } \vee \ldots \vee X _ { k } ) \approx \prod _ { 1 } ^ { \infty } h_{ *} ( X _ { i } ). \end{equation*} | |
| − | Milnor's uniqueness theorem admits an extension for generalized homology theories [[#References|[a1]]]: A homology theory | + | Milnor's uniqueness theorem admits an extension for generalized homology theories [[#References|[a1]]]: A homology theory $h_* $ on $\bf K$ satisfying the Milnor axioms (now without a dimension axiom) is, up to an isomorphism of homology theories, uniquely determined by its restriction to the category of compact absolute neighbourhood retracts $\bf P$ (or polyhedra or CW-spaces). Moreover, every homology theory $h_* $ on $\bf P$ admits a unique extension $h_* ^ { S }$ over $\bf K$ as a Steenrod–Sitnikov homology theory. If $h_{*} ( . ) = \mathbf{E}_{*} ( . )$ (the homology theory with coefficients in a spectrum, $\mathbf{E} = \{ E _ { n } | \sigma : \Sigma : E _ { n } \rightarrow E _ { n + 1} \}$) (cf. also [[Spectrum of spaces|Spectrum of spaces]]), then $h ^ { S_{ * } } ( \cdot ) \approx \overline { \mathbf{E} }_{*} ( \cdot )$ is uniquely determined by the spectrum $\mathbf E$. |
| − | It turns out [[#References|[a1]]] that | + | It turns out [[#References|[a1]]] that $\overline { E }_{*} ( )$ is constructed like ${\bf E}_{ *} ( )$, but with replacing continuous mappings by strong shape mappings. So, Steenrod–Sitnikov homology is defined on a strong shape category (cf. [[Strong shape theory|Strong shape theory]]). |
| − | Steenrod–Sitnikov homology appears as the appropriate tool for handling geometric problems in | + | Steenrod–Sitnikov homology appears as the appropriate tool for handling geometric problems in $\bf K$. This pertains to [[Alexander duality|Alexander duality]] in its most modern form, dealing with homology and cohomology with coefficients in a spectrum, to [[S-duality|$S$-duality]], as well as to dimension theory of subspaces of $S ^ { n }$. |
| − | Ordinary Steenrod–Sitnikov homology appeared for the first time in [[#References|[a6]]] as a tool for Alexander duality. In the 1950s, K. Sitnikov rediscovered | + | Ordinary Steenrod–Sitnikov homology appeared for the first time in [[#References|[a6]]] as a tool for Alexander duality. In the 1950s, K. Sitnikov rediscovered $H _ { * } ^ { S }$ by using a different definition [[#References|[a4]]], [[#References|[a5]]], without knowing about [[#References|[a6]]], and verified an Alexander duality theorem for arbitrary $X \subset S ^ { n}$ by using this kind of homology with compact support. |
As official opponent in Sitnikov's doctoral dissertation, G.S. Chogoshvili pointed out that the homology groups of Sitnikov and Steenrod agree. | As official opponent in Sitnikov's doctoral dissertation, G.S. Chogoshvili pointed out that the homology groups of Sitnikov and Steenrod agree. | ||
| − | Sitnikov's definition of | + | Sitnikov's definition of $H _ { * } ^ { S }$ is modelled after the classical definition of [[Vietoris homology|Vietoris homology]]: A Vietoris cycle $\mathbf{z} ^ { n } = \{ z _ { i } ^ { n } \}$ on a space $X \in \bf K$ consists of a sequence of $\varepsilon_i$-cycles, $\varepsilon _ { i } > 0$ (i.e. each $z _ { i } ^ { n }$ is a cycle with simplices with vertices in $X$ of maximal diameter $< \varepsilon _ { i }$), with $\varepsilon _ { i } \rightarrow 0$, such that $z _ { i } ^ { n } \sim z _ { i + 1 } ^ { n }$ by some $\varepsilon_i$-chain $x _ { * } ^ { n + 1 }$: |
| − | + | \begin{equation*} d x _ { i } ^ { n + 1 } = z _ { i } ^ { n } - z _ { i + 1 } ^ { n }. \end{equation*} | |
| − | A Sitnikov-cycle | + | A Sitnikov-cycle $\mathbf{z} ^ { n } = \{ z _ { i } ^ { n } , x _ { i } ^ { n + 1 } \}$ specifies the chains $x _ { i } ^ { n + 1 }$. So, two Sitnikov cycles |
| − | + | \begin{equation*} \mathbf{z} ^ { n } = \{ z ^ { n _ { i } } , x _ { i } ^ { n + 1 } \} , \overline{\mathbf{z}} \square ^ { n } = \{ z _ { i } ^ { n } , \overline{x} \square _ { i } ^ { n + 1 } \} \end{equation*} | |
give rise to the same Vietoris cycle but eventually to different Sitnikov homology classes. | give rise to the same Vietoris cycle but eventually to different Sitnikov homology classes. | ||
| Line 44: | Line 52: | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> F.W. Bauer, "Extensions of generalized homology theories" ''Pacific J. Math.'' , '''128''' : 1 (1987) pp. 25–61</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> S. Eilenberg, N. Steenrod, "Foundations of algebraic topology" , ''Princeton Math. Ser.'' , '''15''' , Princeton Univ. Press (1952)</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> J. Milnor, "On the Steenrod homology theory" , Berkeley (unpublished)</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> K. Sitnikov, "Combinatorial topology of non-closed sets I" ''Mat. Sb.'' , '''84''' : 76 (1954) pp. 3–54 (In Russian)</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> K. Sitnikov, "Combinatorial topology of non-closed sets I–II" ''Mat. Sb.'' , '''37''' : 79 (1955) pp. 355–434 (In Russian)</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> N. Steenrod, "Regular cycles of compact metric spaces" ''Amer. J. Math.'' , '''41''' (1940) pp. 833–85</td></tr></table> |
Revision as of 15:30, 1 July 2020
A homology theory $h_* ^ { S }$ supposed to be defined on the category of pairs of compact metric (i.e., metrizable) spaces $\bf K$, satisfying all Steenrod–Eilenberg axioms (in the case of generalized Steenrod–Sitnikov homology, without a dimension axiom) together with a strong excision axiom (i.e. $p : ( X , A ) \rightarrow ( X / A , * )$ induces an isomorphism in homology).
For an ordinary Steenrod–Sitnikov homology theory $H _ { * } ^ { S } (\cdot \ ; G )$ ($G$ an Abelian group) J. Milnor [a3] established the following axiomatic characterization: An ordinary homology theory $H _ * (\, . \, ; G )$ on $\bf K$ satisfying the Eilenberg–Steenrod axioms (with strong excision and dimension axiom) and in addition the cluster (or strong wedge) axiom is isomorphic (as a homology theory) to $H _ { * } ^ { S } (\cdot \ ; G )$.
Let $( X _ { i } , x _ { i 0 } ) = X_i$, $i = 1,2 , \dots$, be a family of based spaces in $\bf K$; then the cluster $\operatorname {Cl} _ { i = 1 } ^ { \infty } ( X _ { i } , x _ { i_0 } ) = ( X , x _ { 0 } )$ is the wedge of the $X_i$, equipped with the strong topology (a neighbourhood of the basepoint $x _ { 0 }$ contains almost all $X_i$ or, alternatively, 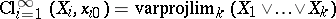 ). The projection $p _ { i } : X \rightarrow X_i$ induces a mapping
). The projection $p _ { i } : X \rightarrow X_i$ induces a mapping
\begin{equation} \tag{a1} H_{*} ( X , x _ { 0 } ; G ) \overset{\approx}{\rightarrow} \prod _ { 1 } ^ { \infty } H_{*} ( X _ { i } , x _ { i 0 } ; G ). \end{equation}
The cluster axiom requires that (a1) be an isomorphism.
The cluster axiom turns out to be some kind of continuity axiom: A homology theory $h_* $ is continuous whenever there is a natural isomorphism
\begin{equation} \tag{a2} \operatorname{varprojlim}_kh * ( X _ { k } ) = h * ( \text { varprojlim } _ { k } X _ { k } ), \end{equation}
i.e. the functor $h_* $ commutes with inverse limits. S. Eilenberg and N. Steenrod [a2] discovered that there is a conflict between (a2) and the exactness axiom, so that no homology theory can be continuous. However, the cluster axiom reveals itself as a special case of (a2): One has
\begin{equation*} \operatorname{varprojlim}_{k}( X _ { 1 } \vee \ldots \vee X _ { k } ) = \operatorname{Cl} _ { i = 1 } ^ { \infty } ( X _ { i } , x _ { i 0 } ). \end{equation*}
and
\begin{equation*} \operatorname { varprojlim}_{k} h_{ *} ( X _ { 1 } \vee \ldots \vee X _ { k } ) \approx \prod _ { 1 } ^ { \infty } h_{ *} ( X _ { i } ). \end{equation*}
Milnor's uniqueness theorem admits an extension for generalized homology theories [a1]: A homology theory $h_* $ on $\bf K$ satisfying the Milnor axioms (now without a dimension axiom) is, up to an isomorphism of homology theories, uniquely determined by its restriction to the category of compact absolute neighbourhood retracts $\bf P$ (or polyhedra or CW-spaces). Moreover, every homology theory $h_* $ on $\bf P$ admits a unique extension $h_* ^ { S }$ over $\bf K$ as a Steenrod–Sitnikov homology theory. If $h_{*} ( . ) = \mathbf{E}_{*} ( . )$ (the homology theory with coefficients in a spectrum, $\mathbf{E} = \{ E _ { n } | \sigma : \Sigma : E _ { n } \rightarrow E _ { n + 1} \}$) (cf. also Spectrum of spaces), then $h ^ { S_{ * } } ( \cdot ) \approx \overline { \mathbf{E} }_{*} ( \cdot )$ is uniquely determined by the spectrum $\mathbf E$.
It turns out [a1] that $\overline { E }_{*} ( )$ is constructed like ${\bf E}_{ *} ( )$, but with replacing continuous mappings by strong shape mappings. So, Steenrod–Sitnikov homology is defined on a strong shape category (cf. Strong shape theory).
Steenrod–Sitnikov homology appears as the appropriate tool for handling geometric problems in $\bf K$. This pertains to Alexander duality in its most modern form, dealing with homology and cohomology with coefficients in a spectrum, to $S$-duality, as well as to dimension theory of subspaces of $S ^ { n }$.
Ordinary Steenrod–Sitnikov homology appeared for the first time in [a6] as a tool for Alexander duality. In the 1950s, K. Sitnikov rediscovered $H _ { * } ^ { S }$ by using a different definition [a4], [a5], without knowing about [a6], and verified an Alexander duality theorem for arbitrary $X \subset S ^ { n}$ by using this kind of homology with compact support.
As official opponent in Sitnikov's doctoral dissertation, G.S. Chogoshvili pointed out that the homology groups of Sitnikov and Steenrod agree.
Sitnikov's definition of $H _ { * } ^ { S }$ is modelled after the classical definition of Vietoris homology: A Vietoris cycle $\mathbf{z} ^ { n } = \{ z _ { i } ^ { n } \}$ on a space $X \in \bf K$ consists of a sequence of $\varepsilon_i$-cycles, $\varepsilon _ { i } > 0$ (i.e. each $z _ { i } ^ { n }$ is a cycle with simplices with vertices in $X$ of maximal diameter $< \varepsilon _ { i }$), with $\varepsilon _ { i } \rightarrow 0$, such that $z _ { i } ^ { n } \sim z _ { i + 1 } ^ { n }$ by some $\varepsilon_i$-chain $x _ { * } ^ { n + 1 }$:
\begin{equation*} d x _ { i } ^ { n + 1 } = z _ { i } ^ { n } - z _ { i + 1 } ^ { n }. \end{equation*}
A Sitnikov-cycle $\mathbf{z} ^ { n } = \{ z _ { i } ^ { n } , x _ { i } ^ { n + 1 } \}$ specifies the chains $x _ { i } ^ { n + 1 }$. So, two Sitnikov cycles
\begin{equation*} \mathbf{z} ^ { n } = \{ z ^ { n _ { i } } , x _ { i } ^ { n + 1 } \} , \overline{\mathbf{z}} \square ^ { n } = \{ z _ { i } ^ { n } , \overline{x} \square _ { i } ^ { n + 1 } \} \end{equation*}
give rise to the same Vietoris cycle but eventually to different Sitnikov homology classes.
There have been attempts to extend Steenrod–Sitnikov homology to more general topological spaces, leading to what is called strong homology. This was initiated for ordinary homology theories by S. Mardešić and Ju. Lisica. There is an analogous axiomatic characterization of strong homology, where one has to replace the cluster axiom by a continuity axiom on the chain level (the c-continuity of a homology theory).
References
| [a1] | F.W. Bauer, "Extensions of generalized homology theories" Pacific J. Math. , 128 : 1 (1987) pp. 25–61 |
| [a2] | S. Eilenberg, N. Steenrod, "Foundations of algebraic topology" , Princeton Math. Ser. , 15 , Princeton Univ. Press (1952) |
| [a3] | J. Milnor, "On the Steenrod homology theory" , Berkeley (unpublished) |
| [a4] | K. Sitnikov, "Combinatorial topology of non-closed sets I" Mat. Sb. , 84 : 76 (1954) pp. 3–54 (In Russian) |
| [a5] | K. Sitnikov, "Combinatorial topology of non-closed sets I–II" Mat. Sb. , 37 : 79 (1955) pp. 355–434 (In Russian) |
| [a6] | N. Steenrod, "Regular cycles of compact metric spaces" Amer. J. Math. , 41 (1940) pp. 833–85 |
Steenrod-Sitnikov homology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Steenrod-Sitnikov_homology&oldid=23041