Difference between revisions of "Total positivity"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 49003 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | < | + | A real-valued function (or kernel) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t110/t110030/t1100301.png" /> on two linearly ordered sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t110/t110030/t1100302.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t110/t110030/t1100303.png" /> is called totally positive if for each positive integer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t110/t110030/t1100304.png" /> and for all |
| − | t1100301.png | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | if | ||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t110/t110030/t1100305.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a1)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
one has | one has | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t110/t110030/t1100306.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a2)</td></tr></table> | |
| − | |||
| − | If both | + | If both <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t110/t110030/t1100307.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t110/t110030/t1100308.png" /> are finite sets, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t110/t110030/t1100309.png" /> can be considered a finite [[Matrix|matrix]] and then one calls it a totally positive matrix. Consequently, a totally positive matrix is a matrix whose minors (cf. [[Minor|Minor]]) are all non-negative. When all the inequalities are strict in these definitions, the matrix or kernel is called strictly totally positive. Some authors replace the term "total positivity" by "totally non-negative matrixtotally non-negative kerneltotal non-negativity" and "strict total positivity" by "total positivity" . When (a2) holds only for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t110/t110030/t11003010.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t110/t110030/t11003011.png" /> is a positive integer, the kernel is called totally positive of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t110/t110030/t11003013.png" />. |
| − | and | ||
| − | are finite sets, then | ||
| − | can be considered a finite [[Matrix|matrix]] and then one calls it a totally positive matrix. Consequently, a totally positive matrix is a matrix whose minors (cf. [[Minor|Minor]]) are all non-negative. When all the inequalities are strict in these definitions, the matrix or kernel is called strictly totally positive. Some authors replace the term "total positivity" by "totally non-negative matrixtotally non-negative kerneltotal non-negativity" and "strict total positivity" by "total positivity" . When (a2) holds only for | ||
| − | where | ||
| − | is a positive integer, the kernel is called totally positive of order | ||
Sign-regularity is an extension of the concept of total positivity. For it, (a2) is replaced by the weaker requirement that | Sign-regularity is an extension of the concept of total positivity. For it, (a2) is replaced by the weaker requirement that | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t110/t110030/t11003014.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a3)</td></tr></table> | |
| − | |||
| − | for a given sequence | + | for a given sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t110/t110030/t11003015.png" /> with each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t110/t110030/t11003016.png" />. In this case <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t110/t110030/t11003017.png" /> is said to be sign-regular of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t110/t110030/t11003020.png" />, with signature sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t110/t110030/t11003021.png" />. Analogously one can define strict sign-regularity. |
| − | with each | ||
| − | In this case | ||
| − | is said to be sign-regular of order | ||
| − | with signature sequence | ||
| − | Analogously one can define strict sign-regularity. | ||
| − | If | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t110/t110030/t11003022.png" /> is a totally positive function of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t110/t110030/t11003023.png" /> of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t110/t110030/t11003024.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t110/t110030/t11003025.png" /> is a called a Pólya frequency function (respectively, a Pólya frequency sequence) of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t110/t110030/t11003026.png" /> when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t110/t110030/t11003027.png" /> (respectively, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t110/t110030/t11003028.png" />, the integers). |
| − | is a totally positive function of order | ||
| − | of the form | ||
| − | then | ||
| − | is a called a Pólya frequency function (respectively, a Pólya frequency sequence) of order | ||
| − | when | ||
| − | respectively, | ||
| − | the integers). | ||
| − | Simple examples of totally positive functions are | + | Simple examples of totally positive functions are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t110/t110030/t11003029.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t110/t110030/t11003030.png" /> and |
| − | with | ||
| − | and | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t110/t110030/t11003031.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | with | + | with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t110/t110030/t11003032.png" />. A well-known example of a strictly totally positive matrix on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t110/t110030/t11003033.png" /> is the Vandermonde matrix (cf. also [[Vandermonde determinant|Vandermonde determinant]]) |
| − | A well-known example of a strictly totally positive matrix on | ||
| − | is the Vandermonde matrix (cf. also [[Vandermonde determinant|Vandermonde determinant]]) | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t110/t110030/t11003034.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | defined for | + | defined for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t110/t110030/t11003035.png" />. |
Generalizations of all these concepts can be found in [[#References|[a4]]]. This useful book has, for many years, been the only one entirely devoted to the theory of total positivity. Interesting historical facts concerning the development of this subject can be found scattered throughout its chapters. | Generalizations of all these concepts can be found in [[#References|[a4]]]. This useful book has, for many years, been the only one entirely devoted to the theory of total positivity. Interesting historical facts concerning the development of this subject can be found scattered throughout its chapters. | ||
Revision as of 14:53, 7 June 2020
A real-valued function (or kernel)  on two linearly ordered sets
on two linearly ordered sets  and
and  is called totally positive if for each positive integer
is called totally positive if for each positive integer  and for all
and for all
 | (a1) |
one has
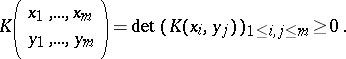 | (a2) |
If both  and
and  are finite sets, then
are finite sets, then  can be considered a finite matrix and then one calls it a totally positive matrix. Consequently, a totally positive matrix is a matrix whose minors (cf. Minor) are all non-negative. When all the inequalities are strict in these definitions, the matrix or kernel is called strictly totally positive. Some authors replace the term "total positivity" by "totally non-negative matrixtotally non-negative kerneltotal non-negativity" and "strict total positivity" by "total positivity" . When (a2) holds only for
can be considered a finite matrix and then one calls it a totally positive matrix. Consequently, a totally positive matrix is a matrix whose minors (cf. Minor) are all non-negative. When all the inequalities are strict in these definitions, the matrix or kernel is called strictly totally positive. Some authors replace the term "total positivity" by "totally non-negative matrixtotally non-negative kerneltotal non-negativity" and "strict total positivity" by "total positivity" . When (a2) holds only for  , where
, where  is a positive integer, the kernel is called totally positive of order
is a positive integer, the kernel is called totally positive of order  .
.
Sign-regularity is an extension of the concept of total positivity. For it, (a2) is replaced by the weaker requirement that
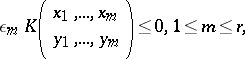 | (a3) |
for a given sequence  with each
with each  . In this case
. In this case 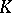 is said to be sign-regular of order
is said to be sign-regular of order  , with signature sequence
, with signature sequence  . Analogously one can define strict sign-regularity.
. Analogously one can define strict sign-regularity.
If  is a totally positive function of order
is a totally positive function of order  of the form
of the form  , then
, then  is a called a Pólya frequency function (respectively, a Pólya frequency sequence) of order
is a called a Pólya frequency function (respectively, a Pólya frequency sequence) of order  when
when  (respectively,
(respectively,  , the integers).
, the integers).
Simple examples of totally positive functions are  with
with  and
and
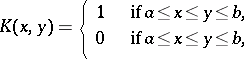 |
with  . A well-known example of a strictly totally positive matrix on
. A well-known example of a strictly totally positive matrix on  is the Vandermonde matrix (cf. also Vandermonde determinant)
is the Vandermonde matrix (cf. also Vandermonde determinant)
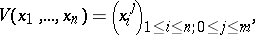 |
defined for  .
.
Generalizations of all these concepts can be found in [a4]. This useful book has, for many years, been the only one entirely devoted to the theory of total positivity. Interesting historical facts concerning the development of this subject can be found scattered throughout its chapters.
The theory of totally positive matrices was developed in the 1930s by F.R. Gantmacher and M.G. Krein in connection with vibrations of mechanical systems. Green functions of certain differential operators provide important examples of totally positive matrices. Independently, I.J. Schoenberg developed the theory of total positivity in connection with the variation diminishing properties of matrices, giving rise to spline theory. Schoenberg also initiated the study of Pólya frequency functions and sequences. Much of this work was influenced by the work of O.D. Kellog, G. Pólya, M. Fekete, T.S. Motzkin to name only a few of the many mathematicians who worked in various aspects of this subject. Spectral properties of totally positive kernels were studied by Gantmacher and Krein. An interesting and detailed discussion of the history of this development with a self-contained presentation of the main results can be found in [a5].
Starting in the late 1950s, S. Karlin began to demonstrate in numerous publications on the subject the breath of application and depth of mathematical importance of total positivity. Under Karlin's influence, many authors have been motivated to investigate the application of total positivity to approximation theory, analysis, statistics, biology, and geometric modeling. See [a6] for a valuable reference source for information on total positivity.
Totally positive matrices form a subclass of the non-negative matrices. See [a1] for a very interesting survey of totally positive matrices up to 1987; it contains many of their properties available up to that time. In 1996 a new book, [a2], appeared, devoted entirely to the theory and applications of total positivity. It is an excellent source of information on the exciting recent developments in the subject with a special emphasis on its applications. For example, it has chapters devoted to the connections between spline functions and total positivity, others to Chebychev spaces, totally positive matrices, combinatorics, statistics, integral equations, geometric modeling, complex analysis and nonlinear analysis.
One of the most recent fields where total positivity has interesting applications is that of geometric modeling. In the design of curves it is useful to be able to predict and control the shape of the curve from the shape of the control polygon of the curve, determined by certain points. There are several articles in [a2] which address this important practical problem.
Totally positive functions arise quite naturally in the theory of diffusion stochastic processes (cf. also Diffusion process). For a birth-and-death process, the transition probability function is totally positive. These questions will be addressed in Volume II of [a4] which, unfortunately, has yet (1996) to appear. A series of papers written by Karlin and J.L. McGregor address this fascinating connection to total positivity, see, for example, [a3].
References
| [a1] | T. Ando, "Totally positive matrices" Linear Alg. & Its Appl. , 90 (1987) pp. 165–219 |
| [a2] | "Total positivity and its applications" M. Gasca (ed.) C.A. Micchelli (ed.) , Kluwer Acad. Publ. (1996) |
| [a3] | S. Karlin, J.L. McGregor, "Classical difussion processes and total positivity" J. Math. Anal. Appl. , 1 (1960) pp. 163–183 |
| [a4] | S. Karlin, "Total positivity" , I , Stanford Univ. Press (1968) |
| [a5] | A. Pinkus, "Spectral properties of totally positive kernels and matrices" M. Gasca (ed.) C.A. Micchelli (ed.) , Total Positivity and its Applications , Kluwer Acad. Publ. (1996) pp. 477–511 |
| [a6] | L.L. Schumaker, "Spline functions: Basic theory" , Wiley (1981) |
Total positivity. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Total_positivity&oldid=49003