Namespaces
Variants
Actions

Difference between revisions of "Suzuki group"

From Encyclopedia of Mathematics
Jump to: navigation, search
m (tex encoded by computer)
m (Undo revision 48916 by Ulf Rehmann (talk))
Tag: Undo
Line 1: Line 1:
−
<!--
+
A [[Simple finite group|simple finite group]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s0915101.png" />, a member of the infinite series of simple groups, discovered by M. Suzuki.
−
s0915101.png
 
−
$#A+1 = 45 n = 0
 
−
$#C+1 = 45 : ~/encyclopedia/old_files/data/S091/S.0901510 Suzuki group
 
−
Automatically converted into TeX, above some diagnostics.
 
−
Please remove this comment and the {{TEX|auto}} line below,
 
−
if TeX found to be correct.
 
−
-->
 
  
−
{{TEX|auto}}
+
Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s0915102.png" /> be a natural number, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s0915103.png" /> be the finite field with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s0915104.png" /> elements, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s0915105.png" /> be an automorphism of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s0915106.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s0915107.png" /> for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s0915108.png" />. The Suzuki group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s0915109.png" /> is then generated by the subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151010.png" /> consisting of all diagonal matrices of order 4 with diagonal elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151011.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151012.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151013.png" />), the subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151014.png" /> consisting of all triangular matrices of the form
−
{{TEX|done}}
 
  
−
A [[Simple finite group|simple finite group]]  $  \mathop{\rm Sz} ( q) $,
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151015.png" /></td> </tr></table>
−
a member of the infinite series of simple groups, discovered by M. Suzuki.
 
  
−
Let  $  n $
+
<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151016.png" />, and the matrix
−
be a natural number, let  $  F $
 
−
be the finite field with  $  q = 2  ^ {2n+} 1 $
 
−
elements, and let  $  \theta $
 
−
be an automorphism of  $  F $
 
−
such that  $  \alpha ^ {\theta  ^ {2} } = \alpha  ^ {2} $
 
−
for any  $  \alpha \in F $.  
 
−
The Suzuki group  $  \mathop{\rm Sz} ( q) $
 
−
is then generated by the subgroup  $  T $
 
−
consisting of all diagonal matrices of order 4 with diagonal elements  $  \lambda ^ {1+ \theta } , \lambda , \lambda  ^ {-} 1 , ( \lambda ^ {1+ \theta } )  ^ {-} 1 $(
 
−
$  \lambda \in F $,
 
−
$  \lambda \neq 0 $),
 
−
the subgroup  $  U $
 
−
consisting of all triangular matrices of the form
 
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151017.png" /></td> </tr></table>
−
\left \|
 
  
−
$  ( \alpha , \beta \in F  ) $,  
+
The subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151018.png" /> is a Sylow <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151019.png" />-subgroup of the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151020.png" />; it is a [[Suzuki-2-group|Suzuki <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151021.png" />-group]]. The subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151022.png" /> coincides with the normalizer of the subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151023.png" />. The permutation representation of the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151024.png" /> on the cosets of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151025.png" /> is doubly transitive; its degree is equal to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151026.png" />. The order of the Suzuki group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151027.png" /> is equal to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151028.png" />, and is not divisible by 3. On the other hand, any non-Abelian finite simple group whose order is not divisible by 3 is isomorphic to a Suzuki group. The group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151029.png" /> is a maximal subgroup of the symplectic group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151030.png" /> and is the centralizer in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151031.png" /> of an automorphism of order 2 of the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151032.png" />. In other words, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151033.png" /> is isomorphic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151034.png" /> — the twisted analogue of a [[Chevalley group|Chevalley group]] of type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151035.png" /> over the field with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151036.png" /> elements.
−
and the matrix
 
  
−
$$
+
====References====
−
\left \|
+
<table><TR><TD valign="top">[1]</TD> <TD valign="top">  M. Suzuki,  "On a class of doubly transitive groups"  ''Ann. of Math.'' , '''75''' :  1  (1962)  pp. 105–145</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top">  R.W. Carter,  "Simple groups of Lie type" , Wiley (Interscience)  (1972)</TD></TR></table>
  
−
The subgroup  $  U $
 
−
is a Sylow  $  2 $-
 
−
subgroup of the group  $  \mathop{\rm Sz} ( q) $;
 
−
it is a [[Suzuki-2-group|Suzuki  $  2 $-
 
−
group]]. The subgroup  $  UT $
 
−
coincides with the normalizer of the subgroup  $  U $.
 
−
The permutation representation of the group  $  \mathop{\rm Sz} ( q) $
 
−
on the cosets of  $  UT $
 
−
is doubly transitive; its degree is equal to  $  q  ^ {2} + 1 $.
 
−
The order of the Suzuki group  $  \mathop{\rm Sz} ( q) $
 
−
is equal to  $  q  ^ {2} ( q- 1)( q  ^ {2} + 1) $,
 
−
and is not divisible by 3. On the other hand, any non-Abelian finite simple group whose order is not divisible by 3 is isomorphic to a Suzuki group. The group  $  \mathop{\rm Sz} ( q) $
 
−
is a maximal subgroup of the symplectic group  $  \mathop{\rm Sp} ( 4, q) $
 
−
and is the centralizer in  $  \mathop{\rm Sp} ( 4, q) $
 
−
of an automorphism of order 2 of the group  $  \mathop{\rm Sp} ( 4, q) = B _ {2} ( q) $.
 
−
In other words,  $  \mathop{\rm Sz} ( q) $
 
−
is isomorphic to  $  {}  ^ {2} B _ {2} ( q) $—
 
−
the twisted analogue of a [[Chevalley group|Chevalley group]] of type  $  B _ {2} $
 
−
over the field with  $  q $
 
−
elements.
 
  
−
====References====
 
−
<table><TR><TD valign="top">[1]</TD> <TD valign="top">  M. Suzuki,  "On a class of doubly transitive groups"  ''Ann. of Math.'' , '''75''' :  1  (1962)  pp. 105–145</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top">  R.W. Carter,  "Simple groups of Lie type" , Wiley (Interscience)  (1972)</TD></TR></table>
 
  
 
====Comments====
 
====Comments====
−
There is in fact precisely one automorphism $  \theta $
+
There is in fact precisely one automorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151037.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151038.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151039.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151040.png" />. It is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151041.png" />.
−
of $  F $
 
−
such that $  \theta  ^ {2} ( \alpha ) = \alpha  ^ {2} $
 
−
for all $  \alpha \in F $.  
 
−
It is $  \theta ( \alpha ) = \alpha ^ {2 ^ {m+ 1 } } $.
 
  
−
There is a twisted polarity whose absolute points are the $  q  ^ {2} + 1 $
+
There is a twisted polarity whose absolute points are the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151042.png" /> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151043.png" />-dimensional subspaces of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151044.png" /> that are fixed by a conjugate of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091510/s09151045.png" />. The set of absolute points thus obtained is an [[Ovoid(2)|ovoid]]. See [[#References|[a1]]]–[[#References|[a2]]].
−
$  1 $-
 
−
dimensional subspaces of $  F _ {q}  ^ {q} $
 
−
that are fixed by a conjugate of $  UT $.  
 
−
The set of absolute points thus obtained is an [[Ovoid(2)|ovoid]]. See [[#References|[a1]]]–[[#References|[a2]]].
 
  
 
====References====
 
====References====
 
<table><TR><TD valign="top">[a1]</TD> <TD valign="top">  J. Tits,  "Ovoïdes et groupes de Suzuki"  ''Arch. Math.'' , '''13'''  (1962)  pp. 187–198</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top">  J. Tits,  "Une propriété charactéristique des ovoïdes associés aux groupes de Suzuki"  ''Arch. Math.'' , '''17'''  (1966)  pp. 136–153</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top">  B. Huppert,  "Finite groups" , '''3''' , Springer  (1982)  pp. Chapt. IX.3</TD></TR></table>
 
<table><TR><TD valign="top">[a1]</TD> <TD valign="top">  J. Tits,  "Ovoïdes et groupes de Suzuki"  ''Arch. Math.'' , '''13'''  (1962)  pp. 187–198</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top">  J. Tits,  "Une propriété charactéristique des ovoïdes associés aux groupes de Suzuki"  ''Arch. Math.'' , '''17'''  (1966)  pp. 136–153</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top">  B. Huppert,  "Finite groups" , '''3''' , Springer  (1982)  pp. Chapt. IX.3</TD></TR></table>

Revision as of 14:53, 7 June 2020

A simple finite group 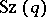, a member of the infinite series of simple groups, discovered by M. Suzuki.

Let be a natural number, let 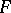be the finite field with 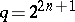elements, and let 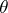be an automorphism of 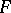such that 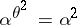for any 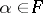. The Suzuki group 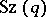is then generated by the subgroup 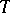consisting of all diagonal matrices of order 4 with diagonal elements 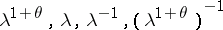(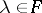, 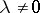), the subgroup 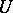consisting of all triangular matrices of the form

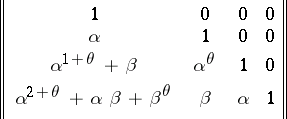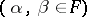, and the matrix

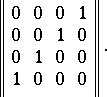The subgroup 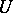is a Sylow -subgroup of the group 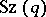; it is a Suzuki -group. The subgroup coincides with the normalizer of the subgroup 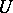. The permutation representation of the group 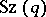on the cosets of 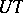is doubly transitive; its degree is equal to 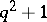. The order of the Suzuki group 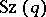is equal to 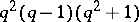, and is not divisible by 3. On the other hand, any non-Abelian finite simple group whose order is not divisible by 3 is isomorphic to a Suzuki group. The group 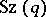is a maximal subgroup of the symplectic group 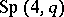and is the centralizer in 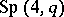of an automorphism of order 2 of the group 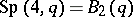. In other words, 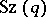is isomorphic to 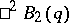— the twisted analogue of a Chevalley group of type 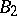over the field with 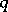elements.

References

[1] M. Suzuki, "On a class of doubly transitive groups" Ann. of Math. , 75 : 1 (1962) pp. 105–145
[2] R.W. Carter, "Simple groups of Lie type" , Wiley (Interscience) (1972)


Comments

There is in fact precisely one automorphism 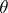of 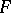such that 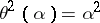for all 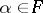. It is .

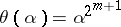There is a twisted polarity whose absolute points are the 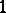-dimensional subspaces of 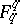that are fixed by a conjugate of . The set of absolute points thus obtained is an ovoid. See [a1]–[a2].

References

[a1] J. Tits, "Ovoïdes et groupes de Suzuki" Arch. Math. , 13 (1962) pp. 187–198
[a2] J. Tits, "Une propriété charactéristique des ovoïdes associés aux groupes de Suzuki" Arch. Math. , 17 (1966) pp. 136–153
[a3] B. Huppert, "Finite groups" , 3 , Springer (1982) pp. Chapt. IX.3
How to Cite This Entry:
Suzuki group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Suzuki_group&oldid=48916
This article was adapted from an original article by V.D. Mazurov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article
Retrieved from "https://encyclopediaofmath.org/index.php?title=Suzuki_group&oldid=49460"