Difference between revisions of "Ring with divided powers"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48573 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | < | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r0824301.png" /> be a commutative ring with unit, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r0824302.png" /> be an augmented <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r0824303.png" />-algebra, i.e. there is given a homomorphism of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r0824304.png" />-algebras <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r0824305.png" />. A divided power structure on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r0824306.png" /> (or, more precisely, on the augmentation ideal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r0824307.png" />) is a sequence of mappings |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r0824308.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
such that | such that | ||
| − | 1) | + | 1) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r0824309.png" />; |
| − | 2) | + | 2) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243010.png" />; |
| − | 3) | + | 3) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243011.png" />; |
| − | 4) | + | 4) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243012.png" />; |
| − | 5) | + | 5) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243013.png" />; |
| − | where | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243014.png" /> in 3) and |
| − | in 3) and | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243015.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | In case | + | In case <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243016.png" /> is a graded commutative algebra over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243017.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243018.png" />, these requirements are augmented as follows (and changed slightly): |
| − | is a graded commutative algebra over | ||
| − | with | ||
| − | these requirements are augmented as follows (and changed slightly): | ||
| − | 6) | + | 6) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243019.png" />, |
with 5) replaced by | with 5) replaced by | ||
| Line 68: | Line 27: | ||
5') | 5') | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243020.png" /></td> </tr></table> | |
| − | Given an | + | Given an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243021.png" />-module <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243022.png" />, an algebra with divided powers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243023.png" /> is constructed as follows. It is generated (as an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243024.png" />-algebra) by symbols <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243025.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243026.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243027.png" /> and between these symbols the following relations are imposed: |
| − | module | ||
| − | an algebra with divided powers | ||
| − | is constructed as follows. It is generated (as an | ||
| − | algebra) by symbols | ||
| − | |||
| − | |||
| − | and between these symbols the following relations are imposed: | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243028.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243029.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243030.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | This | + | This <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243031.png" /> satisfies 1)–5). The augmentation sends <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243032.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243033.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243034.png" />). If one assigns to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243035.png" /> the degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243036.png" />, a graded commutative algebra is obtained with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243037.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243038.png" /> which satisfies 1)–4), 5'), 6). |
| − | satisfies 1)–5). The augmentation sends | ||
| − | to | ||
| − | |||
| − | If one assigns to | ||
| − | the degree | ||
| − | a graded commutative algebra is obtained with | ||
| − | |||
| − | which satisfies 1)–4), 5'), 6). | ||
| − | If | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243039.png" /> is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243040.png" />-algebra, divided powers can always be defined as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243041.png" />. The relations 1)–5) can be understood as a way of writing down the interrelations between such "divided powers" (such as the one resulting from the binomial theorem) without having to use division by integers. |
| − | is a | ||
| − | algebra, divided powers can always be defined as | ||
| − | The relations 1)–5) can be understood as a way of writing down the interrelations between such "divided powers" (such as the one resulting from the binomial theorem) without having to use division by integers. | ||
| − | A divided power sequence in a co-algebra | + | A divided power sequence in a co-algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243042.png" /> is a sequence of elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243043.png" /> satisfying |
| − | is a sequence of elements | ||
| − | satisfying | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082430/r08243044.png" /></td> </tr></table> | |
| − | |||
| − | |||
Divided power sequences are used in the theories of Hopf algebras and formal groups (cf. [[Formal group|Formal group]]; [[Hopf algebra|Hopf algebra]]), [[#References|[a1]]]–[[#References|[a3]]]. Rings with divided powers occur in algebraic topology (where they provide a natural setting for power cohomology operations), [[#References|[a4]]], [[#References|[a5]]], and the theory of formal groups [[#References|[a3]]], [[#References|[a2]]]. | Divided power sequences are used in the theories of Hopf algebras and formal groups (cf. [[Formal group|Formal group]]; [[Hopf algebra|Hopf algebra]]), [[#References|[a1]]]–[[#References|[a3]]]. Rings with divided powers occur in algebraic topology (where they provide a natural setting for power cohomology operations), [[#References|[a4]]], [[#References|[a5]]], and the theory of formal groups [[#References|[a3]]], [[#References|[a2]]]. | ||
Revision as of 14:53, 7 June 2020
Let  be a commutative ring with unit, and let
be a commutative ring with unit, and let  be an augmented
be an augmented  -algebra, i.e. there is given a homomorphism of
-algebra, i.e. there is given a homomorphism of  -algebras
-algebras  . A divided power structure on
. A divided power structure on  (or, more precisely, on the augmentation ideal
(or, more precisely, on the augmentation ideal 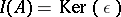 ) is a sequence of mappings
) is a sequence of mappings
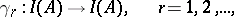 |
such that
1)  ;
;
2)  ;
;
3) 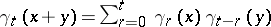 ;
;
4)  ;
;
5)  ;
;
where 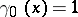 in 3) and
in 3) and
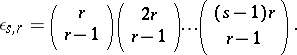 |
In case  is a graded commutative algebra over
is a graded commutative algebra over 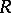 with
with  , these requirements are augmented as follows (and changed slightly):
, these requirements are augmented as follows (and changed slightly):
6)  ,
,
with 5) replaced by
5')
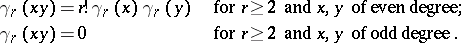 |
Given an  -module
-module  , an algebra with divided powers
, an algebra with divided powers  is constructed as follows. It is generated (as an
is constructed as follows. It is generated (as an  -algebra) by symbols
-algebra) by symbols  ,
, 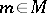 ,
,  and between these symbols the following relations are imposed:
and between these symbols the following relations are imposed:
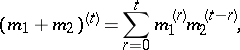 |
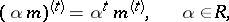 |
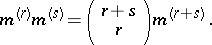 |
This 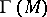 satisfies 1)–5). The augmentation sends
satisfies 1)–5). The augmentation sends  to
to  (
( ). If one assigns to
). If one assigns to  the degree
the degree 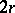 , a graded commutative algebra is obtained with
, a graded commutative algebra is obtained with 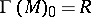 ,
,  which satisfies 1)–4), 5'), 6).
which satisfies 1)–4), 5'), 6).
If  is a
is a  -algebra, divided powers can always be defined as
-algebra, divided powers can always be defined as 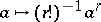 . The relations 1)–5) can be understood as a way of writing down the interrelations between such "divided powers" (such as the one resulting from the binomial theorem) without having to use division by integers.
. The relations 1)–5) can be understood as a way of writing down the interrelations between such "divided powers" (such as the one resulting from the binomial theorem) without having to use division by integers.
A divided power sequence in a co-algebra  is a sequence of elements
is a sequence of elements  satisfying
satisfying
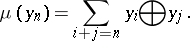 |
Divided power sequences are used in the theories of Hopf algebras and formal groups (cf. Formal group; Hopf algebra), [a1]–[a3]. Rings with divided powers occur in algebraic topology (where they provide a natural setting for power cohomology operations), [a4], [a5], and the theory of formal groups [a3], [a2].
References
| [a1] | N. Roby, "Les algèbres à puissances divisées" Bull. Soc. Math. France , 89 (1965) pp. 75–91 |
| [a2] | M. Hazewinkel, "Formal groups and applications" , Acad. Press (1978) |
| [a3] | P. Cartier, "Exemples d'hyperalgèbres" , Sem. S. Lie 1955/56 , 3 , Secr. Math. Univ. Paris (1957) |
| [a4] | E. Thomas, "The generalized Pontryagin cohomology operations and rings with divided powers" , Amer. Math. Soc. (1957) |
| [a5] | S. Eilenberg, S. MacLane, "On the groups 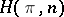 , II" Ann. of Math. , 60 (1954) pp. 49–189 , II" Ann. of Math. , 60 (1954) pp. 49–189 |
Ring with divided powers. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ring_with_divided_powers&oldid=48573