Difference between revisions of "Path"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48142 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | < | + | A [[Continuous mapping|continuous mapping]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p0718101.png" /> of the interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p0718102.png" /> into a [[Topological space|topological space]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p0718103.png" />. The points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p0718104.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p0718105.png" /> are called the initial and the final points of the path <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p0718106.png" />. Given <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p0718107.png" />, the path defined by the formula <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p0718108.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p0718109.png" />, is called the path inverse to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p07181010.png" /> and is denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p07181011.png" />. Given <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p07181012.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p07181013.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p07181014.png" />, the path defined by the formula |
| − | p0718101.png | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p07181015.png" /></td> </tr></table> | |
| − | |||
| − | + | is called the composite of the paths <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p07181016.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p07181017.png" /> and is denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p07181018.png" />. In a [[Path-connected space|path-connected space]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p07181019.png" /> with distinguished point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p07181020.png" />, the set of all paths with initial point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p07181021.png" /> forms the [[Path space|path space]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p07181022.png" />. | |
| − | of the | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | the path | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | Generally one is interested not so much in the individual paths in a space as in the homotopy classes thereof; if one factors by the equivalence relation of homotopy relative to | + | Generally one is interested not so much in the individual paths in a space as in the homotopy classes thereof; if one factors by the equivalence relation of homotopy relative to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p07181023.png" />, the composition defined above becomes associative, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p07181024.png" /> becomes a genuine inverse to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p07181025.png" />. See [[Fundamental groupoid|Fundamental groupoid]]. |
| − | the composition defined above becomes associative, and | ||
| − | becomes a genuine inverse to | ||
| − | See [[Fundamental groupoid|Fundamental groupoid]]. | ||
| − | More precisely, one may define a path as being any continuous mapping | + | More precisely, one may define a path as being any continuous mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p07181026.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p07181027.png" /> is called the length of the path <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p07181028.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p07181029.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p07181030.png" />, with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p07181031.png" /> of length <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p07181032.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p07181033.png" />, are composed to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p07181034.png" />, taking <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p07181035.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p07181036.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p07181037.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p07181038.png" /> (where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p07181039.png" /> has length <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p07181040.png" />) to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071810/p07181041.png" />. This composition is associative (not only homotopy associative). |
| − | where | ||
| − | is called the length of the path | ||
| − | Then | ||
| − | and | ||
| − | with | ||
| − | of length | ||
| − | and | ||
| − | are composed to | ||
| − | taking | ||
| − | to | ||
| − | and | ||
| − | in | ||
| − | where | ||
| − | has length | ||
| − | to | ||
| − | This composition is associative (not only homotopy associative). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P.J. Hilton, S. Wylie, "Homology theory. An introduction to algebraic topology" , Cambridge Univ. Press (1965)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P.J. Hilton, S. Wylie, "Homology theory. An introduction to algebraic topology" , Cambridge Univ. Press (1965)</TD></TR></table> | ||
Revision as of 14:52, 7 June 2020
A continuous mapping 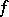 of the interval
of the interval 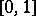 into a topological space
into a topological space 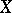 . The points
. The points 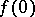 and
and 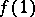 are called the initial and the final points of the path
are called the initial and the final points of the path 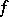 . Given
. Given 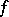 , the path defined by the formula
, the path defined by the formula 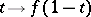 ,
, 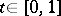 , is called the path inverse to
, is called the path inverse to 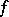 and is denoted by
and is denoted by 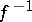 . Given
. Given 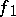 and
and 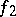 with
with 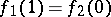 , the path defined by the formula
, the path defined by the formula
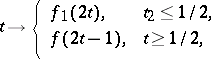 |
is called the composite of the paths 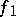 and
and 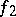 and is denoted by
and is denoted by 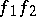 . In a path-connected space
. In a path-connected space 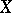 with distinguished point
with distinguished point  , the set of all paths with initial point
, the set of all paths with initial point  forms the path space of
forms the path space of 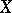 .
.
Comments
Generally one is interested not so much in the individual paths in a space as in the homotopy classes thereof; if one factors by the equivalence relation of homotopy relative to 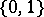 , the composition defined above becomes associative, and
, the composition defined above becomes associative, and 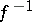 becomes a genuine inverse to
becomes a genuine inverse to 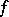 . See Fundamental groupoid.
. See Fundamental groupoid.
More precisely, one may define a path as being any continuous mapping 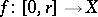 , where
, where 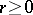 is called the length of the path
is called the length of the path 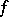 . Then
. Then 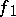 and
and 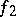 , with
, with 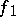 of length
of length  and
and 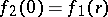 , are composed to
, are composed to 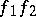 , taking
, taking 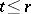 to
to 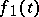 and
and  in
in 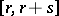 (where
(where 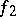 has length
has length  ) to
) to 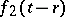 . This composition is associative (not only homotopy associative).
. This composition is associative (not only homotopy associative).
References
| [a1] | P.J. Hilton, S. Wylie, "Homology theory. An introduction to algebraic topology" , Cambridge Univ. Press (1965) |
Path. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Path&oldid=48142