Difference between revisions of "Orthogonal series"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48079 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
A series of the form | A series of the form | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o0703701.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table> | |
| − | |||
| − | |||
| − | where | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o0703702.png" /> is an [[Orthonormal system|orthonormal system]] of functions with respect to a measure <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o0703703.png" />: |
| − | is an [[Orthonormal system|orthonormal system]] of functions with respect to a measure | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o0703704.png" /></td> </tr></table> | |
| − | |||
| − | |||
Since the 18th century, certain special orthonormal systems and expansions of functions with respect to them have appeared in the research of L. Euler, D. Bernoulli, A. Legendre, P. Laplace, F. Bessel, and others into various questions of mathematics, astronomy, mechanics, and physics (planetary motion, oscillation of chords, membranes, etc.). The following have had a decisive influence on the creation of the theory of orthogonal series: | Since the 18th century, certain special orthonormal systems and expansions of functions with respect to them have appeared in the research of L. Euler, D. Bernoulli, A. Legendre, P. Laplace, F. Bessel, and others into various questions of mathematics, astronomy, mechanics, and physics (planetary motion, oscillation of chords, membranes, etc.). The following have had a decisive influence on the creation of the theory of orthogonal series: | ||
| Line 38: | Line 21: | ||
==Characteristic results and directions of research in the theory of orthogonal series.== | ==Characteristic results and directions of research in the theory of orthogonal series.== | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | 1) Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o0703705.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o0703706.png" /> be Lebesgue measure and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o0703707.png" /> be an orthonormal system. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o0703708.png" />, then the numbers | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o0703709.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | are called the Fourier coefficients, while the series (1) with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037010.png" /> is called the Fourier series of the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037011.png" /> with respect to the system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037012.png" />. | |
| − | is | ||
| − | |||
| − | |||
| − | |||
| − | + | The system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037013.png" /> is closed in the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037014.png" /> if for any function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037015.png" /> and any number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037016.png" />, a polynomial | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037017.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | can be found such that the norm <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037018.png" />. The system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037019.png" /> is complete relative to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037020.png" /> if it follows from the conditions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037021.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037022.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037023.png" /> that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037024.png" /> almost-everywhere, i.e. that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037025.png" /> is the zero element of the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037026.png" />. | |
| − | the | ||
| − | + | If for a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037027.png" /> the equation | |
| − | |||
| − | |||
| − | |||
| − | is fulfilled, then the function | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037028.png" /></td> <td valign="top" style="width:5%;text-align:right;">(2)</td></tr></table> |
| − | is said to satisfy the Lyapunov–Steklov closure condition (or Parseval identity). This condition is equivalent to convergence of the partial sums of the Fourier series of | + | |
| − | in the norm of | + | is fulfilled, then the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037029.png" /> is said to satisfy the Lyapunov–Steklov closure condition (or Parseval identity). This condition is equivalent to convergence of the partial sums of the Fourier series of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037030.png" /> in the norm of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037031.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037032.png" />. |
| − | to | ||
The definitions of closure and completeness, and conditions of closure, are given in the same way for more general spaces and measures. | The definitions of closure and completeness, and conditions of closure, are given in the same way for more general spaces and measures. | ||
| − | One of the most important questions in the theory of orthogonal series is the question of the unique determination of a function by means of its Fourier coefficients. For the space | + | One of the most important questions in the theory of orthogonal series is the question of the unique determination of a function by means of its Fourier coefficients. For the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037033.png" /> it is connected very closely to the fulfillment of (2) for all functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037034.png" />. |
| − | it is connected very closely to the fulfillment of (2) for all functions | ||
Equation (2) was put forward in 1805 (though without proof) for the [[Trigonometric system|trigonometric system]] by M. Parseval, while in 1828, Bessel established that | Equation (2) was put forward in 1805 (though without proof) for the [[Trigonometric system|trigonometric system]] by M. Parseval, while in 1828, Bessel established that | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037035.png" /></td> <td valign="top" style="width:5%;text-align:right;">(3)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | (the Bessel inequality). In 1896, A.M. Lyapunov proved (2) for Riemann-integrable functions and P. Fatou then proved it for the case | + | (the Bessel inequality). In 1896, A.M. Lyapunov proved (2) for Riemann-integrable functions and P. Fatou then proved it for the case <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037036.png" />. |
V.A. Steklov (1898–1904) put forward the question of the closure of general orthonormal systems, and solved it positively for many orthogonal systems (spherical functions, eigen functions of a Sturm–Liouville operator, systems of orthogonal Hermite polynomials, Laguerre polynomials, Lamé functions, and others). | V.A. Steklov (1898–1904) put forward the question of the closure of general orthonormal systems, and solved it positively for many orthogonal systems (spherical functions, eigen functions of a Sturm–Liouville operator, systems of orthogonal Hermite polynomials, Laguerre polynomials, Lamé functions, and others). | ||
| − | Inequality (3) has proved to be true for arbitrary orthonormal systems and functions | + | Inequality (3) has proved to be true for arbitrary orthonormal systems and functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037037.png" />. |
| − | In 1907, F. Riesz and E. Fischer proved that for any orthonormal system | + | In 1907, F. Riesz and E. Fischer proved that for any orthonormal system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037038.png" /> and for any sequence of numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037039.png" /> a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037040.png" /> can be found for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037041.png" /> and such that (2) is fulfilled. It follows from this theorem and the Bessel inequality that for any orthonormal system, completeness and closure are equivalent in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037042.png" />; closure in the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037043.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037044.png" /> is equivalent to completeness in the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037045.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037046.png" /> (S. Banach, 1931). |
| − | and for any sequence of numbers | ||
| − | a function | ||
| − | can be found for which | ||
| − | and such that (2) is fulfilled. It follows from this theorem and the Bessel inequality that for any orthonormal system, completeness and closure are equivalent in | ||
| − | closure in the space | ||
| − | with | ||
| − | is equivalent to completeness in the space | ||
| − | where | ||
| − | S. Banach, 1931). | ||
| − | The Bessel inequality and the Riesz–Fischer theorem were extended by G.H. Hardy, J.E. Littlewood and R. Paley to the space | + | The Bessel inequality and the Riesz–Fischer theorem were extended by G.H. Hardy, J.E. Littlewood and R. Paley to the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037047.png" />. In fact, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037048.png" /> be an orthonormal system, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037049.png" />, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037050.png" />. Then: |
| − | In fact, let | ||
| − | be an orthonormal system, | ||
| − | and let | ||
| − | Then: | ||
| − | a) if | + | a) if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037051.png" />, |
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037052.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | b) If a sequence | + | b) If a sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037053.png" /> is given with |
| − | is given with | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037054.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | then a function | + | then a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037055.png" /> can be found for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037056.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037057.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037058.png" /> depends only on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037059.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037060.png" />. |
| − | can be found for which | ||
| − | and | ||
| − | where | ||
| − | depends only on | ||
| − | and | ||
| − | 2) Another important problem in the theory of orthogonal series is the question of the expansion of a function, by means of simple functions, in a series converging to it in the norm of some space. A system of elements | + | 2) Another important problem in the theory of orthogonal series is the question of the expansion of a function, by means of simple functions, in a series converging to it in the norm of some space. A system of elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037061.png" /> from a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037062.png" />-space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037063.png" /> is called a basis (an unconditional basis) if every element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037064.png" /> can be uniquely represented in the form of a series |
| − | from a | ||
| − | space | ||
| − | is called a basis (an unconditional basis) if every element | ||
| − | can be uniquely represented in the form of a series | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037065.png" /></td> <td valign="top" style="width:5%;text-align:right;">(4)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | converging (unconditionally converging) to | + | converging (unconditionally converging) to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037066.png" /> in the norm of the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037067.png" />. |
| − | in the norm of the space | ||
| − | If | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037068.png" /> is a basis in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037069.png" />, then the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037070.png" /> are continuous linear functionals on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037071.png" /> and, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037072.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037073.png" />, take the form |
| − | is a basis in | ||
| − | then the | ||
| − | are continuous linear functionals on | ||
| − | and, if | ||
| − | with | ||
| − | take the form | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037074.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | where | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037075.png" /> is a basis in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037076.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037077.png" /> is a bi-orthonormal system (Banach). In particular, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037078.png" />, i.e. if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037079.png" /> is an orthonormal system, then an orthogonal basis in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037080.png" /> is automatically a basis in all spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037081.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037082.png" /> is any number between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037083.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037084.png" />. |
| − | is a basis in | ||
| − | and | ||
| − | is a bi-orthonormal system (Banach). In particular, if | ||
| − | i.e. if | ||
| − | is an orthonormal system, then an orthogonal basis in | ||
| − | is automatically a basis in all spaces | ||
| − | where | ||
| − | is any number between | ||
| − | and | ||
Research into this problem has followed two directions: | Research into this problem has followed two directions: | ||
| − | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037085.png" />) for a given orthonormal system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037086.png" />, find the spaces in which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037087.png" /> is a basis; | |
| − | for a given orthonormal system | ||
| − | find the spaces in which | ||
| − | is a basis; | ||
| − | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037088.png" />) for a given space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037089.png" />, determine its bases or orthogonal bases. | |
| − | for a given space | ||
| − | determine its bases or orthogonal bases. | ||
| − | In both cases, a mutual connection is sought between the properties of a function | + | In both cases, a mutual connection is sought between the properties of a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037090.png" /> and its expansions. |
| − | and its expansions. | ||
| − | As for the trigonometric system, it is not a basis in the space | + | As for the trigonometric system, it is not a basis in the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037091.png" /> of continuous functions (P. du Bois-Reymond, 1876) but it is a basis in the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037093.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037094.png" /> (M. Riesz, 1927). The du Bois-Reymond result has been extended to all uniformly bounded orthonormal systems. |
| − | of continuous functions (P. du Bois-Reymond, 1876) but it is a basis in the space | ||
| − | with | ||
| − | M. Riesz, 1927). The du Bois-Reymond result has been extended to all uniformly bounded orthonormal systems. | ||
| − | The orthonormal system of Legendre polynomials is a basis in the spaces | + | The orthonormal system of Legendre polynomials is a basis in the spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037095.png" /> when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037096.png" /> and is not so in the other spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037097.png" /> (1946–1952, H. Pollard, J. von Neumann and W. Rudin). |
| − | when | ||
| − | and is not so in the other spaces | ||
| − | 1946–1952, H. Pollard, J. von Neumann and W. Rudin). | ||
| − | In 1910, an orthonormal system | + | In 1910, an orthonormal system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037098.png" /> was created such that every continuous function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o07037099.png" /> can be uniquely expanded in a uniformly converging Fourier series with respect to this system (A. Haar). However, the [[Haar system|Haar system]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370100.png" /> is not a basis in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370101.png" />, since the functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370102.png" /> are discontinuous when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370103.png" />. By integrating the system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370104.png" />, G. Faber (1910) established that the system |
| − | was created such that every continuous function | ||
| − | can be uniquely expanded in a uniformly converging Fourier series with respect to this system (A. Haar). However, the [[Haar system|Haar system]] | ||
| − | is not a basis in | ||
| − | since the functions | ||
| − | are discontinuous when | ||
| − | By integrating the system | ||
| − | G. Faber (1910) established that the system | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370105.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | is a basis in | + | is a basis in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370106.png" /> and thereby the first basis in the space of continuous functions was found. Faber's result was rediscovered by J. Schauder (1927), who also determined a class of bases in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370107.png" /> of the type of the basis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370108.png" />; in honour of the latter, the term "Schauder basisSchauder basis" was introduced, although it would be more correct to call it a "Faber–Schauder basisFaber–Schauder basis" . |
| − | and thereby the first basis in the space of continuous functions was found. Faber's result was rediscovered by J. Schauder (1927), who also determined a class of bases in | ||
| − | of the type of the basis | ||
| − | in honour of the latter, the term "Schauder basisSchauder basis" was introduced, although it would be more correct to call it a "Faber–Schauder basisFaber–Schauder basis" . | ||
| − | These bases are not orthogonal. The first orthonormal basis | + | These bases are not orthogonal. The first orthonormal basis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370109.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370110.png" /> was obtained by Ph. Franklin (1928), who orthogonalized, by the Schmidt method (cf. [[Orthogonalization|Orthogonalization]]), the Faber–Schauder system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370111.png" /> and obtained <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370112.png" />. In this direction (orthogonalization and integration), a new class of bases has been introduced and studied. All orthonormal bases in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370113.png" /> are automatically bases in all spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370114.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370115.png" />. |
| − | in | ||
| − | was obtained by Ph. Franklin (1928), who orthogonalized, by the Schmidt method (cf. [[Orthogonalization|Orthogonalization]]), the Faber–Schauder system | ||
| − | and obtained | ||
| − | In this direction (orthogonalization and integration), a new class of bases has been introduced and studied. All orthonormal bases in | ||
| − | are automatically bases in all spaces | ||
| − | with | ||
| − | The Haar system | + | The Haar system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370116.png" /> is an unconditional basis in all spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370117.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370118.png" /> (1931–1937, Paley, J. Marcinkiewicz). The same result also holds for the Franklin system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370119.png" />. |
| − | is an unconditional basis in all spaces | ||
| − | with | ||
| − | 1931–1937, Paley, J. Marcinkiewicz). The same result also holds for the Franklin system | ||
| − | In the spaces | + | In the spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370120.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370121.png" /> there are no unconditional bases, in general. Neither are there any normalized or uniformly bounded unconditional bases in the spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370122.png" /> when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370123.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370124.png" />. |
| − | and | ||
| − | there are no unconditional bases, in general. Neither are there any normalized or uniformly bounded unconditional bases in the spaces | ||
| − | when | ||
| − | |||
3) Much research has been devoted to the problem of the almost-everywhere convergence of trigonometric and orthogonal series. | 3) Much research has been devoted to the problem of the almost-everywhere convergence of trigonometric and orthogonal series. | ||
| Line 243: | Line 108: | ||
In 1911, N.N. Luzin gave the first example of an almost-everywhere divergent trigonometric series whose coefficients tend to zero. A Fourier series of this type was constructed by A.N. Kolmogorov (1923). Luzin's result has been extended to arbitrary complete orthonormal systems, while Kolmogorov's result has been generalized to sets of positive measure for uniformly bounded orthonormal systems. | In 1911, N.N. Luzin gave the first example of an almost-everywhere divergent trigonometric series whose coefficients tend to zero. A Fourier series of this type was constructed by A.N. Kolmogorov (1923). Luzin's result has been extended to arbitrary complete orthonormal systems, while Kolmogorov's result has been generalized to sets of positive measure for uniformly bounded orthonormal systems. | ||
| − | A non-negative sequence | + | A non-negative sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370125.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370126.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370127.png" /> is called a Weyl multiplier for the almost-everywhere convergence of a series with respect to a system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370128.png" /> if every series (1) converges almost everywhere on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370129.png" />, when only |
| − | with | ||
| − | |||
| − | is called a Weyl multiplier for the almost-everywhere convergence of a series with respect to a system | ||
| − | if every series (1) converges almost everywhere on | ||
| − | when only | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370130.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | If | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370131.png" /> is a Weyl multiplier, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370132.png" /> is called a system of almost-everywhere convergence. The sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370133.png" /> is called an exact Weyl multiplier for the almost-everywhere convergence of a series (1) if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370134.png" /> is a Weyl multiplier, while every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370135.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370136.png" />, is not. Definitions of a Weyl multiplier for other forms of convergence and summability are given in the same way (convergence in measure, unconditional convergence almost-everywhere, and others). |
| − | is a Weyl multiplier, then | ||
| − | is called a system of almost-everywhere convergence. The sequence | ||
| − | is called an exact Weyl multiplier for the almost-everywhere convergence of a series (1) if | ||
| − | is a Weyl multiplier, while every | ||
| − | |||
| − | is not. Definitions of a Weyl multiplier for other forms of convergence and summability are given in the same way (convergence in measure, unconditional convergence almost-everywhere, and others). | ||
| − | Weyl multipliers have been found for some systems. In 1913, M. Plancherel proved that | + | Weyl multipliers have been found for some systems. In 1913, M. Plancherel proved that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370137.png" /> is a Weyl multiplier for the almost-everywhere convergence of a series with respect to any orthonormal system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370138.png" />, while in 1922, D.E. Men'shov and H. Rademacher established that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370139.png" /> can be taken as a Weyl multiplier. Most importantly, Men'shov proved that this result could not be improved upon in the whole class of orthonormal systems, i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370140.png" /> is an exact Weyl multiplier for certain orthonormal systems. |
| − | is a Weyl multiplier for the almost-everywhere convergence of a series with respect to any orthonormal system | ||
| − | while in 1922, D.E. Men'shov and H. Rademacher established that | ||
| − | can be taken as a Weyl multiplier. Most importantly, Men'shov proved that this result could not be improved upon in the whole class of orthonormal systems, i.e. | ||
| − | is an exact Weyl multiplier for certain orthonormal systems. | ||
| − | Necessary and sufficient conditions have subsequently been found for | + | Necessary and sufficient conditions have subsequently been found for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370141.png" /> to be a Weyl multiplier for almost-everywhere (in the mean, etc.) convergence or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370142.png" />-summability of orthogonal series. It has been demonstrated, for example, that the system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370143.png" /> is not a system of almost-everywhere convergence. In 1975, the first complete orthonormal system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370144.png" /> of strong convergence i.e. the series (1) converges almost-everywhere on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370145.png" /> if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370146.png" />, was constructed. |
| − | to be a Weyl multiplier for almost-everywhere (in the mean, etc.) convergence or | ||
| − | summability of orthogonal series. It has been demonstrated, for example, that the system | ||
| − | is not a system of almost-everywhere convergence. In 1975, the first complete orthonormal system | ||
| − | of strong convergence i.e. the series (1) converges almost-everywhere on | ||
| − | if and only if | ||
| − | was constructed. | ||
| − | In 1927 it was established that the sequence | + | In 1927 it was established that the sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370147.png" /> is a Weyl multiplier for almost-everywhere unconditional convergence of any orthogonal series if |
| − | is a Weyl multiplier for almost-everywhere unconditional convergence of any orthogonal series if | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370148.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
This result can not be strengthened. | This result can not be strengthened. | ||
| − | In 1960 it was demonstrated that the Haar system | + | In 1960 it was demonstrated that the Haar system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370149.png" /> is not a system of almost-everywhere unconditional convergence. It was also demonstrated, on the basis of this result, that many systems (bases in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370150.png" />, complete orthonormal systems, etc.) are not systems of almost-everywhere unconditional convergence. For the system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370151.png" />, a sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370152.png" /> is a Weyl multiplier for almost-everywhere unconditional convergence only if |
| − | is not a system of almost-everywhere unconditional convergence. It was also demonstrated, on the basis of this result, that many systems (bases in | ||
| − | complete orthonormal systems, etc.) are not systems of almost-everywhere unconditional convergence. For the system | ||
| − | a sequence | ||
| − | is a Weyl multiplier for almost-everywhere unconditional convergence only if | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370153.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
For this reason, not every complete orthonormal system has an exact Weyl multiplier for almost-everywhere unconditional convergence. | For this reason, not every complete orthonormal system has an exact Weyl multiplier for almost-everywhere unconditional convergence. | ||
| − | A great deal of research has been carried out into the problem of the representation of functions by series converging almost-everywhere, in measure or in other ways. So, in 1957 it was established that for any complete orthonormal system | + | A great deal of research has been carried out into the problem of the representation of functions by series converging almost-everywhere, in measure or in other ways. So, in 1957 it was established that for any complete orthonormal system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370154.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370155.png" /> and any measurable function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370156.png" /> there is a series of the form (1) which converges in measure to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070370/o070370157.png" /> (in the case of the trigonometric system this assertion was obtained in 1947 by Men'shov). This result becomes invalid, even in the case of bounded measurable functions, if instead of convergence in measure, almost-everywhere convergence is considered. |
| − | with | ||
| − | and any measurable function | ||
| − | there is a series of the form (1) which converges in measure to | ||
| − | in the case of the trigonometric system this assertion was obtained in 1947 by Men'shov). This result becomes invalid, even in the case of bounded measurable functions, if instead of convergence in measure, almost-everywhere convergence is considered. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> N.N. Luzin, "The integral and trigonometric series" , Moscow-Leningrad (1915) (In Russian) (Thesis; also: Collected Works, Vol. 1, Moscow, 1953, pp. 48–212)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S. Banach, "Théorie des opérations linéaires" , Chelsea, reprint (1955)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> Ya.L. Geronimus, "Orthogonal polynomials" , Consultants Bureau (1961) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> S. Kaczmarz, H. Steinhaus, "Theorie der Orthogonalreihen" , Chelsea, reprint (1951)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> D. Jackson, "Fourier series and orthogonal polynomials" , ''Carus Math. Monogr.'' , '''6''' , Math. Assoc. Amer. (1971)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> G. Szegö, "Orthogonal polynomials" , Amer. Math. Soc. (1975)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> G. Alexits, "Konvergenzprobleme der Orthogonalreihen" , Ungar. Akad. Wissenschaft. (1961)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> F.G. Tricomi, "Vorlesungen über Orthogonalreihen" , Springer (1970) (Translated from Italian)</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> A.M. Olevskii, "Fourier series with respect to general orthogonal systems" , Springer (1975) (Translated from Russian)</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> D.E. Men'shov, P.L. Ul'yanov, "On the metric theory of functions at Moscow University over 50 years" ''Vestnik Moskov. Univ. Ser. 1. Mat. Mekh.'' , '''5''' (1967) pp. 24–36 (In Russian)</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> A.A. Talalyan, "The representation of measurable functions by series" ''Russian Math. Surveys'' , '''15''' : 5 (1960) pp. 75–136 ''Uspekhi Mat. Nauk'' , '''15''' : 5 (1960) pp. 77–141</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> P.L. Ul'yanov, "Solved and unsolved problems in the theory of trigonometric and orthogonal series" ''Russian Math. Surveys'' , '''19''' : 1 (1964) pp. 1–62 ''Uspekhi Mat. Nauk'' , '''19''' : 1 (1964) pp. 3–69</TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> ''J. Soviet Math.'' , '''1''' : 6 (1973) ''Itogi Nauk. Mat. Anal. 1970'' (1971)</TD></TR><TR><TD valign="top">[14]</TD> <TD valign="top"> N. Bourbaki, "Eléments d'histoire des mathématiques" , Hermann (1974)</TD></TR><TR><TD valign="top">[15]</TD> <TD valign="top"> A.B. Paplauskas, "Trigonometric series from Euler to Lebesgue" , Moscow (1966) (In Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> N.N. Luzin, "The integral and trigonometric series" , Moscow-Leningrad (1915) (In Russian) (Thesis; also: Collected Works, Vol. 1, Moscow, 1953, pp. 48–212)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S. Banach, "Théorie des opérations linéaires" , Chelsea, reprint (1955)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> Ya.L. Geronimus, "Orthogonal polynomials" , Consultants Bureau (1961) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> S. Kaczmarz, H. Steinhaus, "Theorie der Orthogonalreihen" , Chelsea, reprint (1951)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> D. Jackson, "Fourier series and orthogonal polynomials" , ''Carus Math. Monogr.'' , '''6''' , Math. Assoc. Amer. (1971)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> G. Szegö, "Orthogonal polynomials" , Amer. Math. Soc. (1975)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> G. Alexits, "Konvergenzprobleme der Orthogonalreihen" , Ungar. Akad. Wissenschaft. (1961)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> F.G. Tricomi, "Vorlesungen über Orthogonalreihen" , Springer (1970) (Translated from Italian)</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> A.M. Olevskii, "Fourier series with respect to general orthogonal systems" , Springer (1975) (Translated from Russian)</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> D.E. Men'shov, P.L. Ul'yanov, "On the metric theory of functions at Moscow University over 50 years" ''Vestnik Moskov. Univ. Ser. 1. Mat. Mekh.'' , '''5''' (1967) pp. 24–36 (In Russian)</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> A.A. Talalyan, "The representation of measurable functions by series" ''Russian Math. Surveys'' , '''15''' : 5 (1960) pp. 75–136 ''Uspekhi Mat. Nauk'' , '''15''' : 5 (1960) pp. 77–141</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> P.L. Ul'yanov, "Solved and unsolved problems in the theory of trigonometric and orthogonal series" ''Russian Math. Surveys'' , '''19''' : 1 (1964) pp. 1–62 ''Uspekhi Mat. Nauk'' , '''19''' : 1 (1964) pp. 3–69</TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> ''J. Soviet Math.'' , '''1''' : 6 (1973) ''Itogi Nauk. Mat. Anal. 1970'' (1971)</TD></TR><TR><TD valign="top">[14]</TD> <TD valign="top"> N. Bourbaki, "Eléments d'histoire des mathématiques" , Hermann (1974)</TD></TR><TR><TD valign="top">[15]</TD> <TD valign="top"> A.B. Paplauskas, "Trigonometric series from Euler to Lebesgue" , Moscow (1966) (In Russian)</TD></TR></table> | ||
| + | |||
| + | |||
====Comments==== | ====Comments==== | ||
For (Weyl) multipliers see also [[Multiplier theory|Multiplier theory]]. | For (Weyl) multipliers see also [[Multiplier theory|Multiplier theory]]. | ||
Revision as of 14:52, 7 June 2020
A series of the form
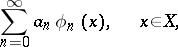 | (1) |
where 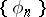 is an orthonormal system of functions with respect to a measure
is an orthonormal system of functions with respect to a measure  :
:
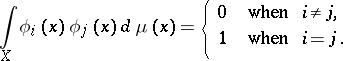 |
Since the 18th century, certain special orthonormal systems and expansions of functions with respect to them have appeared in the research of L. Euler, D. Bernoulli, A. Legendre, P. Laplace, F. Bessel, and others into various questions of mathematics, astronomy, mechanics, and physics (planetary motion, oscillation of chords, membranes, etc.). The following have had a decisive influence on the creation of the theory of orthogonal series:
a) The research of J. Fourier (1807–1822) (the Fourier method for solving the boundary value problems of mathematical physics) and the related work of J. Sturm and J. Liouville (1837–1841);
b) The research of P.L. Chebyshev on interpolation and the problem of moments (mid-19th century), which led to his creation of the general theory of orthogonal polynomials;
c) The research of D. Hilbert (early 20th century) on integral equations (cf. Integral equation with symmetric kernel), in which he established, in particular, general theorems on the expansion of functions in a series with respect to an orthonormal system;
d) The creation by H. Lebesgue of measure theory and the Lebesgue integral, which were responsible for the theory of orthogonal series in its modern form.
The active development of the theory of orthogonal series in the 20th century has been enhanced by the use of orthonormal systems of functions and series with respect to them in the most varied areas of science (mathematical physics, computational mathematics, functional analysis, quantum mechanics, mathematical statistics, operational calculus, automatic regulation and control, various technical problems, etc.).
Characteristic results and directions of research in the theory of orthogonal series.
1) Let  , let
, let 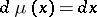 be Lebesgue measure and let
be Lebesgue measure and let 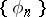 be an orthonormal system. If
be an orthonormal system. If 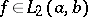 , then the numbers
, then the numbers
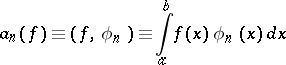 |
are called the Fourier coefficients, while the series (1) with 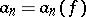 is called the Fourier series of the function
is called the Fourier series of the function  with respect to the system
with respect to the system 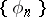 .
.
The system  is closed in the space
is closed in the space 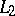 if for any function
if for any function 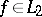 and any number
and any number 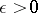 , a polynomial
, a polynomial
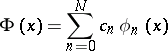 |
can be found such that the norm 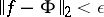 . The system
. The system  is complete relative to
is complete relative to 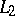 if it follows from the conditions
if it follows from the conditions 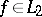 and
and 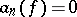 for all
for all 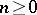 that
that 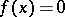 almost-everywhere, i.e. that
almost-everywhere, i.e. that  is the zero element of the space
is the zero element of the space 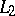 .
.
If for a function  the equation
the equation
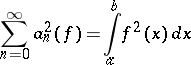 | (2) |
is fulfilled, then the function 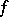 is said to satisfy the Lyapunov–Steklov closure condition (or Parseval identity). This condition is equivalent to convergence of the partial sums of the Fourier series of
is said to satisfy the Lyapunov–Steklov closure condition (or Parseval identity). This condition is equivalent to convergence of the partial sums of the Fourier series of 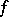 in the norm of
in the norm of 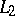 to
to 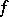 .
.
The definitions of closure and completeness, and conditions of closure, are given in the same way for more general spaces and measures.
One of the most important questions in the theory of orthogonal series is the question of the unique determination of a function by means of its Fourier coefficients. For the space 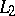 it is connected very closely to the fulfillment of (2) for all functions
it is connected very closely to the fulfillment of (2) for all functions  .
.
Equation (2) was put forward in 1805 (though without proof) for the trigonometric system by M. Parseval, while in 1828, Bessel established that
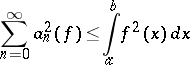 | (3) |
(the Bessel inequality). In 1896, A.M. Lyapunov proved (2) for Riemann-integrable functions and P. Fatou then proved it for the case 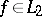 .
.
V.A. Steklov (1898–1904) put forward the question of the closure of general orthonormal systems, and solved it positively for many orthogonal systems (spherical functions, eigen functions of a Sturm–Liouville operator, systems of orthogonal Hermite polynomials, Laguerre polynomials, Lamé functions, and others).
Inequality (3) has proved to be true for arbitrary orthonormal systems and functions 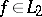 .
.
In 1907, F. Riesz and E. Fischer proved that for any orthonormal system 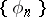 and for any sequence of numbers
and for any sequence of numbers  a function
a function 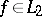 can be found for which
can be found for which 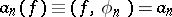 and such that (2) is fulfilled. It follows from this theorem and the Bessel inequality that for any orthonormal system, completeness and closure are equivalent in
and such that (2) is fulfilled. It follows from this theorem and the Bessel inequality that for any orthonormal system, completeness and closure are equivalent in 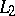 ; closure in the space
; closure in the space 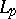 with
with 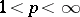 is equivalent to completeness in the space
is equivalent to completeness in the space 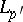 , where
, where 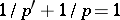 (S. Banach, 1931).
(S. Banach, 1931).
The Bessel inequality and the Riesz–Fischer theorem were extended by G.H. Hardy, J.E. Littlewood and R. Paley to the space 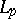 . In fact, let
. In fact, let 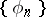 be an orthonormal system,
be an orthonormal system, 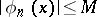 , and let
, and let 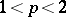 . Then:
. Then:
a) if 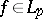 ,
,
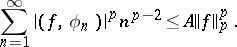 |
b) If a sequence 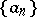 is given with
is given with
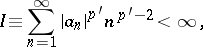 |
then a function  can be found for which
can be found for which 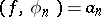 and
and 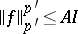 , where
, where 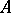 depends only on
depends only on 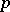 and
and 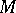 .
.
2) Another important problem in the theory of orthogonal series is the question of the expansion of a function, by means of simple functions, in a series converging to it in the norm of some space. A system of elements 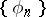 from a
from a 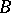 -space
-space 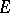 is called a basis (an unconditional basis) if every element
is called a basis (an unconditional basis) if every element 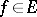 can be uniquely represented in the form of a series
can be uniquely represented in the form of a series
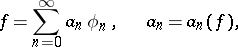 | (4) |
converging (unconditionally converging) to 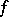 in the norm of the space
in the norm of the space 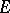 .
.
If 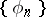 is a basis in
is a basis in  , then the
, then the 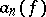 are continuous linear functionals on
are continuous linear functionals on 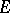 and, if
and, if 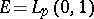 with
with 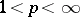 , take the form
, take the form
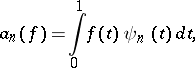 |
where 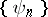 is a basis in
is a basis in  and
and 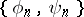 is a bi-orthonormal system (Banach). In particular, if
is a bi-orthonormal system (Banach). In particular, if 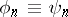 , i.e. if
, i.e. if  is an orthonormal system, then an orthogonal basis in
is an orthonormal system, then an orthogonal basis in 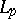 is automatically a basis in all spaces
is automatically a basis in all spaces 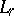 , where
, where  is any number between
is any number between 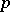 and
and 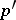 .
.
Research into this problem has followed two directions:
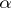 ) for a given orthonormal system
) for a given orthonormal system 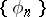 , find the spaces in which
, find the spaces in which 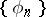 is a basis;
is a basis;
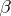 ) for a given space
) for a given space  , determine its bases or orthogonal bases.
, determine its bases or orthogonal bases.
In both cases, a mutual connection is sought between the properties of a function 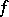 and its expansions.
and its expansions.
As for the trigonometric system, it is not a basis in the space 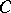 of continuous functions (P. du Bois-Reymond, 1876) but it is a basis in the space
of continuous functions (P. du Bois-Reymond, 1876) but it is a basis in the space 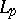 with
with 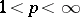 (M. Riesz, 1927). The du Bois-Reymond result has been extended to all uniformly bounded orthonormal systems.
(M. Riesz, 1927). The du Bois-Reymond result has been extended to all uniformly bounded orthonormal systems.
The orthonormal system of Legendre polynomials is a basis in the spaces 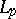 when
when 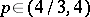 and is not so in the other spaces
and is not so in the other spaces  (1946–1952, H. Pollard, J. von Neumann and W. Rudin).
(1946–1952, H. Pollard, J. von Neumann and W. Rudin).
In 1910, an orthonormal system 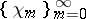 was created such that every continuous function
was created such that every continuous function 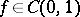 can be uniquely expanded in a uniformly converging Fourier series with respect to this system (A. Haar). However, the Haar system
can be uniquely expanded in a uniformly converging Fourier series with respect to this system (A. Haar). However, the Haar system 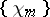 is not a basis in
is not a basis in 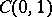 , since the functions
, since the functions 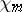 are discontinuous when
are discontinuous when 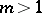 . By integrating the system
. By integrating the system 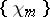 , G. Faber (1910) established that the system
, G. Faber (1910) established that the system
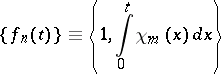 |
is a basis in  and thereby the first basis in the space of continuous functions was found. Faber's result was rediscovered by J. Schauder (1927), who also determined a class of bases in
and thereby the first basis in the space of continuous functions was found. Faber's result was rediscovered by J. Schauder (1927), who also determined a class of bases in 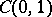 of the type of the basis
of the type of the basis 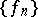 ; in honour of the latter, the term "Schauder basisSchauder basis" was introduced, although it would be more correct to call it a "Faber–Schauder basisFaber–Schauder basis" .
; in honour of the latter, the term "Schauder basisSchauder basis" was introduced, although it would be more correct to call it a "Faber–Schauder basisFaber–Schauder basis" .
These bases are not orthogonal. The first orthonormal basis  in
in 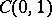 was obtained by Ph. Franklin (1928), who orthogonalized, by the Schmidt method (cf. Orthogonalization), the Faber–Schauder system
was obtained by Ph. Franklin (1928), who orthogonalized, by the Schmidt method (cf. Orthogonalization), the Faber–Schauder system 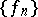 and obtained
and obtained 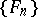 . In this direction (orthogonalization and integration), a new class of bases has been introduced and studied. All orthonormal bases in
. In this direction (orthogonalization and integration), a new class of bases has been introduced and studied. All orthonormal bases in 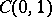 are automatically bases in all spaces
are automatically bases in all spaces 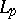 with
with 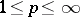 .
.
The Haar system 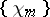 is an unconditional basis in all spaces
is an unconditional basis in all spaces 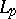 with
with 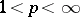 (1931–1937, Paley, J. Marcinkiewicz). The same result also holds for the Franklin system
(1931–1937, Paley, J. Marcinkiewicz). The same result also holds for the Franklin system 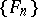 .
.
In the spaces 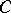 and
and 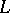 there are no unconditional bases, in general. Neither are there any normalized or uniformly bounded unconditional bases in the spaces
there are no unconditional bases, in general. Neither are there any normalized or uniformly bounded unconditional bases in the spaces 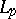 when
when 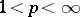 and
and 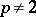 .
.
3) Much research has been devoted to the problem of the almost-everywhere convergence of trigonometric and orthogonal series.
In 1911, N.N. Luzin gave the first example of an almost-everywhere divergent trigonometric series whose coefficients tend to zero. A Fourier series of this type was constructed by A.N. Kolmogorov (1923). Luzin's result has been extended to arbitrary complete orthonormal systems, while Kolmogorov's result has been generalized to sets of positive measure for uniformly bounded orthonormal systems.
A non-negative sequence 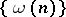 with
with 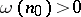 and
and  is called a Weyl multiplier for the almost-everywhere convergence of a series with respect to a system
is called a Weyl multiplier for the almost-everywhere convergence of a series with respect to a system 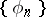 if every series (1) converges almost everywhere on
if every series (1) converges almost everywhere on  , when only
, when only
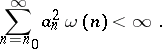 |
If 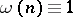 is a Weyl multiplier, then
is a Weyl multiplier, then 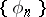 is called a system of almost-everywhere convergence. The sequence
is called a system of almost-everywhere convergence. The sequence 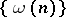 is called an exact Weyl multiplier for the almost-everywhere convergence of a series (1) if
is called an exact Weyl multiplier for the almost-everywhere convergence of a series (1) if  is a Weyl multiplier, while every
is a Weyl multiplier, while every 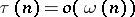 ,
, 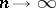 , is not. Definitions of a Weyl multiplier for other forms of convergence and summability are given in the same way (convergence in measure, unconditional convergence almost-everywhere, and others).
, is not. Definitions of a Weyl multiplier for other forms of convergence and summability are given in the same way (convergence in measure, unconditional convergence almost-everywhere, and others).
Weyl multipliers have been found for some systems. In 1913, M. Plancherel proved that 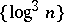 is a Weyl multiplier for the almost-everywhere convergence of a series with respect to any orthonormal system
is a Weyl multiplier for the almost-everywhere convergence of a series with respect to any orthonormal system 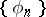 , while in 1922, D.E. Men'shov and H. Rademacher established that
, while in 1922, D.E. Men'shov and H. Rademacher established that 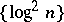 can be taken as a Weyl multiplier. Most importantly, Men'shov proved that this result could not be improved upon in the whole class of orthonormal systems, i.e.
can be taken as a Weyl multiplier. Most importantly, Men'shov proved that this result could not be improved upon in the whole class of orthonormal systems, i.e.  is an exact Weyl multiplier for certain orthonormal systems.
is an exact Weyl multiplier for certain orthonormal systems.
Necessary and sufficient conditions have subsequently been found for 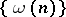 to be a Weyl multiplier for almost-everywhere (in the mean, etc.) convergence or
to be a Weyl multiplier for almost-everywhere (in the mean, etc.) convergence or 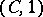 -summability of orthogonal series. It has been demonstrated, for example, that the system
-summability of orthogonal series. It has been demonstrated, for example, that the system 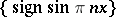 is not a system of almost-everywhere convergence. In 1975, the first complete orthonormal system
is not a system of almost-everywhere convergence. In 1975, the first complete orthonormal system 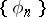 of strong convergence i.e. the series (1) converges almost-everywhere on
of strong convergence i.e. the series (1) converges almost-everywhere on 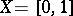 if and only if
if and only if 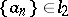 , was constructed.
, was constructed.
In 1927 it was established that the sequence 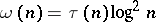 is a Weyl multiplier for almost-everywhere unconditional convergence of any orthogonal series if
is a Weyl multiplier for almost-everywhere unconditional convergence of any orthogonal series if
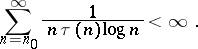 |
This result can not be strengthened.
In 1960 it was demonstrated that the Haar system 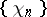 is not a system of almost-everywhere unconditional convergence. It was also demonstrated, on the basis of this result, that many systems (bases in
is not a system of almost-everywhere unconditional convergence. It was also demonstrated, on the basis of this result, that many systems (bases in 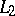 , complete orthonormal systems, etc.) are not systems of almost-everywhere unconditional convergence. For the system
, complete orthonormal systems, etc.) are not systems of almost-everywhere unconditional convergence. For the system 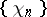 , a sequence
, a sequence 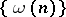 is a Weyl multiplier for almost-everywhere unconditional convergence only if
is a Weyl multiplier for almost-everywhere unconditional convergence only if
 |
For this reason, not every complete orthonormal system has an exact Weyl multiplier for almost-everywhere unconditional convergence.
A great deal of research has been carried out into the problem of the representation of functions by series converging almost-everywhere, in measure or in other ways. So, in 1957 it was established that for any complete orthonormal system 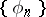 with
with 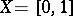 and any measurable function
and any measurable function 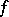 there is a series of the form (1) which converges in measure to
there is a series of the form (1) which converges in measure to 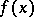 (in the case of the trigonometric system this assertion was obtained in 1947 by Men'shov). This result becomes invalid, even in the case of bounded measurable functions, if instead of convergence in measure, almost-everywhere convergence is considered.
(in the case of the trigonometric system this assertion was obtained in 1947 by Men'shov). This result becomes invalid, even in the case of bounded measurable functions, if instead of convergence in measure, almost-everywhere convergence is considered.
References
| [1] | N.N. Luzin, "The integral and trigonometric series" , Moscow-Leningrad (1915) (In Russian) (Thesis; also: Collected Works, Vol. 1, Moscow, 1953, pp. 48–212) |
| [2] | S. Banach, "Théorie des opérations linéaires" , Chelsea, reprint (1955) |
| [3] | Ya.L. Geronimus, "Orthogonal polynomials" , Consultants Bureau (1961) (Translated from Russian) |
| [4] | S. Kaczmarz, H. Steinhaus, "Theorie der Orthogonalreihen" , Chelsea, reprint (1951) |
| [5] | D. Jackson, "Fourier series and orthogonal polynomials" , Carus Math. Monogr. , 6 , Math. Assoc. Amer. (1971) |
| [6] | G. Szegö, "Orthogonal polynomials" , Amer. Math. Soc. (1975) |
| [7] | G. Alexits, "Konvergenzprobleme der Orthogonalreihen" , Ungar. Akad. Wissenschaft. (1961) |
| [8] | F.G. Tricomi, "Vorlesungen über Orthogonalreihen" , Springer (1970) (Translated from Italian) |
| [9] | A.M. Olevskii, "Fourier series with respect to general orthogonal systems" , Springer (1975) (Translated from Russian) |
| [10] | D.E. Men'shov, P.L. Ul'yanov, "On the metric theory of functions at Moscow University over 50 years" Vestnik Moskov. Univ. Ser. 1. Mat. Mekh. , 5 (1967) pp. 24–36 (In Russian) |
| [11] | A.A. Talalyan, "The representation of measurable functions by series" Russian Math. Surveys , 15 : 5 (1960) pp. 75–136 Uspekhi Mat. Nauk , 15 : 5 (1960) pp. 77–141 |
| [12] | P.L. Ul'yanov, "Solved and unsolved problems in the theory of trigonometric and orthogonal series" Russian Math. Surveys , 19 : 1 (1964) pp. 1–62 Uspekhi Mat. Nauk , 19 : 1 (1964) pp. 3–69 |
| [13] | J. Soviet Math. , 1 : 6 (1973) Itogi Nauk. Mat. Anal. 1970 (1971) |
| [14] | N. Bourbaki, "Eléments d'histoire des mathématiques" , Hermann (1974) |
| [15] | A.B. Paplauskas, "Trigonometric series from Euler to Lebesgue" , Moscow (1966) (In Russian) |
Comments
For (Weyl) multipliers see also Multiplier theory.
Orthogonal series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Orthogonal_series&oldid=48079