|
|
| Line 1: |
Line 1: |
| − | <!--
| + | ''left (right)'' |
| − | n0668901.png
| |
| − | $#A+1 = 67 n = 0
| |
| − | $#C+1 = 67 : ~/encyclopedia/old_files/data/N066/N.0606890 Nomography
| |
| − | Automatically converted into TeX, above some diagnostics.
| |
| − | Please remove this comment and the {{TEX|auto}} line below,
| |
| − | if TeX found to be correct.
| |
| − | -->
| |
| | | | |
| − | {{TEX|auto}}
| + | A [[Ring|ring]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066850/n0668501.png" /> satisfying one of the following equivalent conditions: |
| − | {{TEX|done}}
| |
| | | | |
| − | A branch of mathematics in which methods of graphical representation of functional dependencies are studied. The resulting designs are called nomograms. Every nomogram is constructed for a definite functional dependence within specific limits of variation of the variables. In nomography computational work is replaced by the performance of the simplest geometric operations indicated in the instructions and an evaluation of the answers.
| + | 1) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066850/n0668502.png" /> is a left (or right) [[Noetherian module|Noetherian module]] over itself; |
| | | | |
| − | The accuracy of answers by nomography depends on the form of the nomographic presentation of the dependency, the limits of variation of the variables, the dimension of the design, and on the chosen type of nomogram. On the average, nomograms can provide answers to 2–3 true digits. When the accuracy of nomograms is insufficient, they can be used for provisional calculations, for finding zero-order approximations, and for the control of computations with the aim of discovering gross errors.
| + | 2) every left (or right) ideal in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066850/n0668503.png" /> has a finite generating set; |
| | | | |
| − | Nomograms can also be used to study functional dependencies, putting the nomograms at their foundation. Often such a study can be carried out by nomograms in a considerably simpler and more intuitive way than by other methods. By means of nomograms one can investigate the influence of various variables on the required variable, give an intuitive interpretation of some previously known properties of the dependency in question, and establish previously unknown peculiarities of it. Nomographic methods of investigation can be applied, for example, in problems on the selection of parameters in empirical formulas on the results of observations, in the approximation of one function by another, and for finding extremal values of functions.
| + | 3) every strictly ascending chain of left (or right) ideals in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066850/n0668504.png" /> breaks off after finitely many terms. |
| | | | |
| − | The values of variables are represented in nomograms by marked points and marked lines. A set of marked points depending on a single variable is called a scale. The equation of scale of a variable $ \alpha _ {1} $
| + | An example of a Noetherian ring is any principal ideal ring, i.e. a ring in which every ideal has one generator. |
| − | in a rectangular coordinate system $ x 0 y $ | |
| − | is written in the form
| |
| | | | |
| − | $$
| + | Noetherian rings are named after E. Noether, who made a systematic study of such rings and carried over to them a number of results known earlier only under more stringent restrictions (for example, Lasker's theory of primary decompositions). |
| − | x = f _ {1} ,\ \
| |
| − | y = g _ {1} ,
| |
| − | $$
| |
| | | | |
| − | where $ f _ {1} $
| + | A right Noetherian ring need not be left Noetherian and vice versa. For example, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066850/n0668505.png" /> be the ring of matrices of the form |
| − | and $ g _ {1} $ | |
| − | are functions $ f _ {1} ( \alpha _ {1} ) $
| |
| − | and $ g _ {1} ( \alpha _ {1} ) $.
| |
| − | The scheme of the scale of $ \alpha _ {1} $
| |
| − | is illustrated in Fig. a.
| |
| | | | |
| − | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/n066890a.gif" /> | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066850/n0668506.png" /></td> </tr></table> |
| | | | |
| − | Figure: n066890a
| + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066850/n0668507.png" /> is a rational integer and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066850/n0668508.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066850/n0668509.png" /> are rational numbers, with the usual addition and multiplication. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066850/n06685010.png" /> is right, but not left, Noetherian, since the left ideal of elements of the form |
| | | | |
| − | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/n066890b.gif" /> | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066850/n06685011.png" /></td> </tr></table> |
| | | | |
| − | Figure: n066890b
| + | does not have a finite generating set. |
| | | | |
| − | A set of marked points depending on two variables is called a binary field. A binary field is usually formed as a grid consisting of two families of marked lines. A point in a binary field is determined as the intersection of lines with given marks. In a rectangular coordinate system $ x 0 y $
| + | Quotient rings and finite direct sums of Noetherian rings are again Noetherian, but a subring of a Noetherian ring need not be Noetherian. For example, a polynomial ring in infinitely many variables over a field is not Noetherian, although it is contained in its field of fractions, which is Noetherian. |
| − | the binary field of two variables $ \alpha _ {1} $
| |
| − | and $ \alpha _ {2} $
| |
| − | is given by equations | |
| | | | |
| − | $$
| + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066850/n06685012.png" /> is a left Noetherian ring, then so is the polynomial ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066850/n06685013.png" />. The corresponding property holds for the ring of formal power series over a Noetherian ring. In particular, polynomial rings of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066850/n06685014.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066850/n06685015.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066850/n06685016.png" /> is a field and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066850/n06685017.png" /> the ring of integers, and also quotient rings of them, are Noetherian. Every [[Artinian ring|Artinian ring]] is Noetherian. The localization of a commutative Noetherian ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066850/n06685018.png" /> relative to some multiplicative system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066850/n06685019.png" /> is again Noetherian. If in a commutative Noetherian ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066850/n06685020.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066850/n06685021.png" /> is an ideal such that no element of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066850/n06685022.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066850/n06685023.png" />, is a divisor of zero, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066850/n06685024.png" />. This means that any such ideal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066850/n06685025.png" /> defines on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066850/n06685026.png" /> a separable <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066850/n06685027.png" />-adic topology. In a commutative Noetherian ring every ideal has a representation as an incontractible intersection of finitely many primary ideals. Although such a representation is not unique, the number of ideals and the set of prime ideals associated with the given primary ideals are uniquely determined. |
| − | x = f _ {12} ,\ \
| |
| − | y = g _ {12} ,
| |
| − | $$
| |
| − | | |
| − | where $ f _ {12} $
| |
| − | and $ g _ {12} $
| |
| − | are functions $ f _ {12} ( \alpha _ {1} , \alpha _ {2} ) $
| |
| − | and $ g _ {12} ( \alpha _ {1} , \alpha _ {2} ) $.
| |
| − | It is assumed that $ f _ {12} $
| |
| − | and $ g _ {12} $
| |
| − | are such that in the given domain of variation of the variables to every pair of values $ \alpha _ {1} $
| |
| − | and $ \alpha _ {2} $
| |
| − | corresponds only one pair of values $ x $
| |
| − | and $ y $.
| |
| − | The scheme of a binary field $ ( \alpha _ {1} , \alpha _ {2} ) $
| |
| − | is illustrated in Fig. b.
| |
| − | | |
| − | Scales, families of marked lines and binary fields are formed so that it is convenient to find points and lines with given marks and to determine the marks of answer points and lines.
| |
| − | | |
| − | Elementary nomograms are those in which the answer or answers can be found as a result of performing a single geometric operation (determining a point on a scale or in a binary field; drawing a line through two points; constructing a circle with given centre and radius; dividing a segment in a given ratio; drawing a line parallel to a given one; laying off a segment of length equal to that of a given segment; or superimposing one plane to another).
| |
| − | | |
| − | To the elementary nomograms belong: the graph of a function; scale doubling alignment; nomograms from adjusted points; nomograms from equidistant points; nomograms using a compass; nomograms with parallel indices; barycentric nomograms; rhomboidal nomograms; nomograms with an oriented transparency; and nomograms with a transparency of general form. Key
| |
| − | | |
| − | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/n066890c.gif" /> | |
| − | | |
| − | Figure: n066890c
| |
| − | | |
| − | In Fig. can elementary nomogram is drawn from adjusted points for the determination of the quantity $ x $
| |
| − | from the equation
| |
| − | | |
| − | $$
| |
| − | x ^ {a-} 1 = b
| |
| − | | |
| − | \frac{ \mathop{\rm ln} ( c - x ) }{c - x - 1 }
| |
| − | ,
| |
| − | $$
| |
| − | | |
| − | which is used for thermal calculations involving ventilators. The nomogram is constructed within the limits: $ 0 . 3 \leq a \leq 0 . 8 $;
| |
| − | $ 0 . 1 \leq b \leq 20 $;
| |
| − | $ 0 . 1 \leq c \leq 20 $;
| |
| − | $ 0.001 \leq x < 0 .5 $.
| |
| − | The variables $ a $
| |
| − | and $ b $
| |
| − | are represented on the nomogram by scales; the variables $ c $
| |
| − | and $ x $
| |
| − | by a binary field. The nomogram shows the solution of a numerical example (data: $ a = 0 . 75 $;
| |
| − | $ b = 7 $;
| |
| − | $ c = 10 $;
| |
| − | answer: $ x = 0 . 1 $).
| |
| − | | |
| − | Elementary nomograms have a simple geometric foundation: the nomographic interpretation of the condition that three points are collinear leads to a nomogram from adjusted points; the formulas for the distance between two points — to a nomogram from equidistant points and to the use of a compass; the formulas for the coordinates of a point dividing a segment in a given ratio — to a barycentric nomogram; the condition that two lines are parallel — to a nomogram with parallel indices; the formulas determining the coordinates of the fourth vertex of a parallelogram from three given vertices of it — to a rhomboidal nomogram; the formulas for the transformation of rectangular coordinates with, or without, rotation of the axes — a nomogram on two planes (with an oriented transparency or of general form).
| |
| − | | |
| − | To every elementary nomogram corresponds a canonical form of dependency that can be illustrated by the nomogram. Some canonical forms allow the construction of elementary nomograms of various types.
| |
| − | | |
| − | The most general canonical form represented by an elementary nomogram of adjusted points is
| |
| − | | |
| − | $$
| |
| − | | |
| − | \frac{f _ {34} - f _ {12} }{g _ {34} - g _ {12} }
| |
| − | = \
| |
| − | | |
| − | \frac{f _ {56} - f _ {12} }{g _ {56} - g _ {12} }
| |
| − | .
| |
| − | $$
| |
| − | | |
| − | The corresponding nomogram consists of three binary fields $ ( \alpha _ {1} , \alpha _ {2} ) $,
| |
| − | $ ( \alpha _ {3} , \alpha _ {4} ) $
| |
| − | and $ ( \alpha _ {5} , \alpha _ {6} ) $,
| |
| − | connected by a single alignment.
| |
| − | | |
| − | Below the frequently occurring canonical forms for individual equations and systems of equations representable by nomograms of one type or another are presented.
| |
| − | | |
| − | Canonical forms for individual equations: a) with three variables:
| |
| − | | |
| − | $$
| |
| − | f _ {1} = f _ {23} ,\ \
| |
| − | f _ {1} f _ {3} + f _ {2} g _ {3} + h _ {3} = 0 ,\ \
| |
| − | f _ {1} + f _ {2} = f _ {3} ,\ \
| |
| − | f _ {1} = f _ {2} f _ {3} ;
| |
| − | $$
| |
| − | | |
| − | b) with four variables:
| |
| − | | |
| − | $$
| |
| − | f _ {12} = f _ {34} ,\ \
| |
| − | f _ {1} f _ {34} + f _ {2} g _ {34} + h _ {34} = 0 ,\ \
| |
| − | f _ {12} = f _ {3} + f _ {4} ;
| |
| − | $$
| |
| − | | |
| − | c) with five variables:
| |
| − | | |
| − | $$
| |
| − | f _ {12} = f _ {34} + f _ {35} ; \ \
| |
| − | f _ {1} + f _ {2} + f _ {3} + f _ {4} + f _ {5} = 0 ,
| |
| − | $$
| |
| − | | |
| − | $$
| |
| − | f _ {5} = F ( f _ {12} + f _ {34} , g _ {12} + g _ {34} ) ;
| |
| − | $$
| |
| − | | |
| − | d) with six variables:
| |
| − | | |
| − | $$
| |
| − | f _ {12} + f _ {13} = f _ {45} + f _ {46} ,\ \
| |
| − | f _ {1} + f _ {2} + f _ {3} + f _ {4} + f _ {5} + f _ {6} = 0 ;
| |
| − | $$
| |
| − | | |
| − | e) with seven variables:
| |
| − | | |
| − | $$
| |
| − | f _ {7} = F ( f _ {12} + f _ {34} + f _ {56} , g _ {12} + g _ {31} + g _ {56} ) ,
| |
| − | $$
| |
| − | | |
| − | $$
| |
| − | f _ {1} + f _ {2} + f _ {3} + f _ {4} + f _ {5} + f _ {6} + f _ {7} = 0 .
| |
| − | $$
| |
| − | | |
| − | Canonical forms for systems of equations:
| |
| − | | |
| − | $$
| |
| − | \left . \begin{array}{c}
| |
| − | | |
| − | f _ {3} = f _ {12} ,
| |
| − | \\
| |
| − | | |
| − | g _ {4} = g _ {12} ;
| |
| − |
| |
| − | \end{array}
| |
| − | \right \} \ \
| |
| − | \left . \begin{array}{c}
| |
| − | | |
| − | f _ {12} + f _ {34} = f _ {56} ,
| |
| − | \\
| |
| − | | |
| − | g _ {12} + g _ {34} = g _ {56} ;
| |
| − |
| |
| − | \end{array}
| |
| − | \right \} \ \
| |
| − | \left . \begin{array}{c}
| |
| − | | |
| − | f _ {12} - f _ {56} = f _ {34} - f _ {56} ,
| |
| − | \\
| |
| − | | |
| − | g _ {12} - g _ {56} = g _ {34} - g _ {78} ;
| |
| − |
| |
| − | \end{array}
| |
| − | \right \}
| |
| − | $$
| |
| − | | |
| − | $$
| |
| − | \left . \begin{array}{c}
| |
| − | f _ {12} - g _ {7} = f _ {34} - f _ {8} = f _ {56} - f _ {9} , \\
| |
| − | g _ {12} - g _ {7} = g _ {34} -
| |
| − | g _ {8} = g _ {56} - g _ {9} .
| |
| − | \end{array}
| |
| − | \right \}
| |
| − | $$
| |
| − | | |
| − | Composite nomograms consist of elementary nomograms of the same type or of several types. The introduction of composite nomograms considerably extends the class of dependencies that can be represented nomographically. For a summary of canonical forms that can be represented by elementary and composite nomograms see [[#References|[3]]] and [[#References|[4]]].
| |
| − | | |
| − | A dependency with three variables can always be represented nomographically. Dependencies with four or more variables allow the construction of nomograms only in special cases.
| |
| − | | |
| − | To extend the range of nomographically-representable dependencies one uses approximate representations. One such is based on allowing the given dependency to be nomographed with a certain admissible error. $ Q $,
| |
| − | $ \textrm{ m } ^ {3} / \mathop{\rm sec} $,
| |
| − | $ v \textrm{ m } / \mathop{\rm sec} $,
| |
| − | data
| |
| − | | |
| − | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/n066890d.gif" /> | |
| − | | |
| − | Figure: n066890d
| |
| − | | |
| − | In Fig. dan approximate nomogram from equidistant points is drawn for the determination of the quantities $ \eta $
| |
| − | and $ v $(
| |
| − | or $ Q $
| |
| − | and $ v $)
| |
| − | from the system of equations
| |
| − | | |
| − | $$
| |
| − | \left . \begin{array}{c}
| |
| − | | |
| − | Q = \left ( 76 . 9 + 17 . 72 \mathop{\rm log}
| |
| − | \frac{b \eta }{1 + 2 \eta }
| |
| − | | |
| − | \right )
| |
| − | | |
| − | \frac{b ^ {2.5} \eta ^ {1.5} i ^ {0.5} }{( 1 + 2 \eta ) ^ {0.5} }
| |
| − | ,
| |
| − | \\
| |
| − | | |
| − | v = \left ( 76 . 9 + 17 . 72 \mathop{\rm log}
| |
| − | \frac{b \eta }{1 + 2 \eta }
| |
| − | | |
| − | \right )
| |
| − | | |
| − | \frac{b ^ {0.5} \eta ^ {0.5} i ^ {0.5} }{( 1 + 2 \eta ) ^ {0.5} }
| |
| − | ,
| |
| − |
| |
| − | \end{array}
| |
| − | \right \}
| |
| − | $$
| |
| − | | |
| − | which is used for the calculation of rectangular flows in hydraulics. To use nomography this system was replaced by the approximate system
| |
| − | | |
| − | $$
| |
| − | Q = \
| |
| − | | |
| − | \frac{76 b ^ {2.616} \eta ^ {1.616} i ^ {0.5} }{( 1 + 2 \eta ) ^ {0.616} }
| |
| − | ,\ \
| |
| − | v = \
| |
| − | | |
| − | \frac{76 b ^ {0.616} \eta ^ {0.616} i ^ {0.5} }{( 1 + 2 \eta ) ^ {0.616} }
| |
| − | ,
| |
| − | $$
| |
| − | | |
| − | with a relative error in $ Q $
| |
| − | and $ v $
| |
| − | not exceeding $ 2 . 5\pct $.
| |
| − | The dotted circle in the nomogram corresponds to the solution of a numerical example (data: $ i = 0 . 0005 $;
| |
| − | $ b = 2 \textrm{ m } $;
| |
| − | $ Q = 2 . 2 \textrm{ m } ^ {3} / \mathop{\rm sec} $;
| |
| − | answers: $ \eta = 0 . 5 $
| |
| − | and $ v = 1 . 1 \textrm{ m } / \mathop{\rm sec} $).
| |
| − | | |
| − | In some cases the methods of approximate nomography make it possible to represent a table with several entries by nomograms.
| |
| − | | |
| − | To obtain the nomographic representation of a given dependency one puts it accurately or approximately into nomographic form and writes down the equations of the elements of the nomogram in a rectangular coordinate system. The transformation parameters occurring in these equations (and sometimes also arbitrary functions) are chosen so that they give to the nomogram a form convenient to use. Next one calculates tables of coordinates of the individual elements of the nomogram and then one draws the nomogram.
| |
| − | | |
| − | Machine nomography has been developed (see [[#References|[4]]]–[[#References|[6]]]): Systems of procedures and of standard programs have been worked out for the automatic calculation and construction of elementary nomograms by means of computers and graphical construction as well as standard programs for the automatic construction, calculation and sketching of nomograms of various types.
| |
| − | | |
| − | The main problems of theoretical nomography are representability and uniqueness. The essence of the first problem consists in clarifying whether a given equation or system of equations can be brought to some canonical form and, if possible, to determine an algorithm for this process. Solutions of this problem have been obtained for certain canonical forms. They are cumbersome and seldom used in practice. The essence of the second problem consists in finding out whether there is a unique way of bringing a given dependency to canonical form, and when it is not unique to indicate all possible ways and for each of them to establish whether the nomogram can be transformed into it.
| |
| − | | |
| − | ====References====
| |
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> M.V. Pentkovskii, "Nomography" , Moscow-Leningrad (1949) (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> B.A. Neveskii, "Handbook of nomography" , Moscow-Leningrad (1951) (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> G.S. Khovanskii, "Eléments de nomographie" , MIR (1979) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> G.S. Khovanskii, "Nomography and its possibilities" , Moscow (1977) (In Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> G.S. Khovanskii (ed.) , ''Nomography collection'' , '''15''' , Moscow (1986) (In Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> G.S. Khovanskii, "Nomography today" , Moscow (1987) (In Russian)</TD></TR></table> | |
| − | | |
| − | ====Comments====
| |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> K. Rektorys (ed.) , ''Survey of applicable mathematics'' , Iliffe (1969) pp. Sect. 32A</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R. Sauer (ed.) I. Szabó (ed.) , ''Mathematische Hilfsmittel des Ingenieurs'' , '''III''' , Springer (1967) pp. Sect. G.I.3</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> D.S. Davis, "Nomography and empirical relations" , Wiley (1962)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> A.S. Levens, "Nomography" , Wiley (1959)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> L. Johnson, "Nomography and empirical equations" , Wiley (1952)</TD></TR></table> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> B.L. van der Waerden, "Algebra" , '''1–2''' , Springer (1967–1971) (Translated from German)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S. Lang, "Algebra" , Addison-Wesley (1974)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> C. Faith, "Algebra: rings, modules, and categories" , '''1''' , Springer (1973)</TD></TR></table> |
left (right)
A ring  satisfying one of the following equivalent conditions:
satisfying one of the following equivalent conditions:
1)  is a left (or right) Noetherian module over itself;
is a left (or right) Noetherian module over itself;
2) every left (or right) ideal in  has a finite generating set;
has a finite generating set;
3) every strictly ascending chain of left (or right) ideals in  breaks off after finitely many terms.
breaks off after finitely many terms.
An example of a Noetherian ring is any principal ideal ring, i.e. a ring in which every ideal has one generator.
Noetherian rings are named after E. Noether, who made a systematic study of such rings and carried over to them a number of results known earlier only under more stringent restrictions (for example, Lasker's theory of primary decompositions).
A right Noetherian ring need not be left Noetherian and vice versa. For example, let  be the ring of matrices of the form
be the ring of matrices of the form
where  is a rational integer and
is a rational integer and  and
and  are rational numbers, with the usual addition and multiplication. Then
are rational numbers, with the usual addition and multiplication. Then 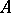 is right, but not left, Noetherian, since the left ideal of elements of the form
is right, but not left, Noetherian, since the left ideal of elements of the form
does not have a finite generating set.
Quotient rings and finite direct sums of Noetherian rings are again Noetherian, but a subring of a Noetherian ring need not be Noetherian. For example, a polynomial ring in infinitely many variables over a field is not Noetherian, although it is contained in its field of fractions, which is Noetherian.
If  is a left Noetherian ring, then so is the polynomial ring
is a left Noetherian ring, then so is the polynomial ring  . The corresponding property holds for the ring of formal power series over a Noetherian ring. In particular, polynomial rings of the form
. The corresponding property holds for the ring of formal power series over a Noetherian ring. In particular, polynomial rings of the form 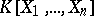 or
or  , where
, where  is a field and
is a field and  the ring of integers, and also quotient rings of them, are Noetherian. Every Artinian ring is Noetherian. The localization of a commutative Noetherian ring
the ring of integers, and also quotient rings of them, are Noetherian. Every Artinian ring is Noetherian. The localization of a commutative Noetherian ring  relative to some multiplicative system
relative to some multiplicative system  is again Noetherian. If in a commutative Noetherian ring
is again Noetherian. If in a commutative Noetherian ring 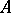 ,
, 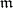 is an ideal such that no element of the form
is an ideal such that no element of the form 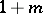 , where
, where 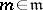 , is a divisor of zero, then
, is a divisor of zero, then  . This means that any such ideal
. This means that any such ideal 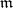 defines on
defines on 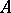 a separable
a separable  -adic topology. In a commutative Noetherian ring every ideal has a representation as an incontractible intersection of finitely many primary ideals. Although such a representation is not unique, the number of ideals and the set of prime ideals associated with the given primary ideals are uniquely determined.
-adic topology. In a commutative Noetherian ring every ideal has a representation as an incontractible intersection of finitely many primary ideals. Although such a representation is not unique, the number of ideals and the set of prime ideals associated with the given primary ideals are uniquely determined.
References
| [1] | B.L. van der Waerden, "Algebra" , 1–2 , Springer (1967–1971) (Translated from German) |
| [2] | S. Lang, "Algebra" , Addison-Wesley (1974) |
| [3] | C. Faith, "Algebra: rings, modules, and categories" , 1 , Springer (1973) |
 satisfying one of the following equivalent conditions:
satisfying one of the following equivalent conditions:
 is a left (or right) Noetherian module over itself;
is a left (or right) Noetherian module over itself;
 has a finite generating set;
has a finite generating set;
 breaks off after finitely many terms.
breaks off after finitely many terms.
 be the ring of matrices of the form
be the ring of matrices of the form
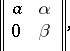
 is a rational integer and
is a rational integer and  and
and  are rational numbers, with the usual addition and multiplication. Then
are rational numbers, with the usual addition and multiplication. Then 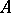 is right, but not left, Noetherian, since the left ideal of elements of the form
is right, but not left, Noetherian, since the left ideal of elements of the form
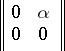
 is a left Noetherian ring, then so is the polynomial ring
is a left Noetherian ring, then so is the polynomial ring  . The corresponding property holds for the ring of formal power series over a Noetherian ring. In particular, polynomial rings of the form
. The corresponding property holds for the ring of formal power series over a Noetherian ring. In particular, polynomial rings of the form 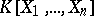 or
or  , where
, where  is a field and
is a field and  the ring of integers, and also quotient rings of them, are Noetherian. Every Artinian ring is Noetherian. The localization of a commutative Noetherian ring
the ring of integers, and also quotient rings of them, are Noetherian. Every Artinian ring is Noetherian. The localization of a commutative Noetherian ring  relative to some multiplicative system
relative to some multiplicative system  is again Noetherian. If in a commutative Noetherian ring
is again Noetherian. If in a commutative Noetherian ring 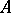 ,
, 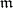 is an ideal such that no element of the form
is an ideal such that no element of the form 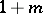 , where
, where 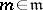 , is a divisor of zero, then
, is a divisor of zero, then  . This means that any such ideal
. This means that any such ideal 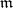 defines on
defines on 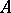 a separable
a separable  -adic topology. In a commutative Noetherian ring every ideal has a representation as an incontractible intersection of finitely many primary ideals. Although such a representation is not unique, the number of ideals and the set of prime ideals associated with the given primary ideals are uniquely determined.
-adic topology. In a commutative Noetherian ring every ideal has a representation as an incontractible intersection of finitely many primary ideals. Although such a representation is not unique, the number of ideals and the set of prime ideals associated with the given primary ideals are uniquely determined.